题目描述

        给你一个字符串 s，找到 s 中最长的回文子串。

解答

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        # 思路一：中心拓展
        def extend_from_center(left,right):
            # 从中心向两侧检测回文
            while left>=0 and right < len(s) and s[left]==s[right]:
                left-=1
                right+=1
            return s[left+1:right]
        # 预先声明longest_palindrome
        longest_palindrome = ""
        for i in range(0,len(s)):
            # 奇数回文子串
            palindrome1=extend_from_center(i,i)
            # 偶数回文子串
            palindrome2=extend_from_center(i,i+1)
            # 迭代最长回文串
            longest_palindrome=max(longest_palindrome, palindrome1, palindrome2, key=len)
        return longest_palindrome

        # # 思路二：动态规划
        # n = len(s)
        # if n <= 1:
        #     return s  # 单字符或空字符串直接返回
        # # 初始化 dp 表，dp[i][j] 表示 s[i:j+1] 是否是回文
        # dp = [[False] * n for _ in range(n)]
        # start, max_length = 0, 1  # 记录最长回文子串的起始位置和长度
        # # 所有长度为 1 的子串是回文
        # for i in range(n):
        #     dp[i][i] = True
        # # 判断所有长度为 2 的子串是否是回文
        # for i in range(n - 1):
        #     if s[i] == s[i + 1]:
        #         dp[i][i + 1] = True
        #         start, max_length = i, 2  # 更新最长回文子串的起始位置和长度
        # # 判断长度大于 2 的子串是否是回文
        # for length in range(3, n + 1):  # 子串长度从 3 到 n
        #     for i in range(n - length + 1):  # 起始位置
        #         j = i + length - 1  # 结束位置
        #         # 状态转移方程
        #         if s[i] == s[j] and dp[i + 1][j - 1]:
        #             dp[i][j] = True
        #             start, max_length = i, length  # 更新最长回文子串的起始位置和长度
        # # 返回最长回文子串
        # return s[start:start + max_length]


        # # 思路三：暴力解法，遍历所有可能的子串
        # # 初始化最长回文子串
        # longest_palindrome = ""
        # # 遍历所有可能的子串
        # for i in range(len(s)):
        #     for j in range(i, len(s)):
        #         # 获取当前子串
        #         current_substring = s[i:j + 1]
        #         # 检查当前子串是否是回文
        #         if current_substring == current_substring[::-1]:  # 判断回文
        #             # 如果是回文，并且长度大于当前最长回文，则更新
        #             if len(current_substring) > len(longest_palindrome):
        #                 longest_palindrome = current_substring
        
        # return longest_palindrome

        思路一，中心拓展法：分奇偶两种情况进行，主要思路是对每个字符及其相邻字符作为中心，向左右两侧扩展，检查形成的最长回文子串。其时间复杂度为O(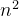)，因为其对每个字符及其相邻字符作为中心进行扩展，共有 O(n) 个中心，每次扩展的最坏情况是 O(n)；其空间复杂度为O(1)，因为只使用了常数空间来存储结果，无需额外存储。

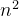
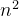
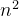
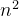
        思路二，动态规划法：使用二维数组 dp[i][j] 表示子串 s[i:j+1] 是否是回文。通过递推公式 dp[i][j] = (s[i] == s[j] and dp[i+1][j-1]) 判断每个子串是否是回文，并记录最长的回文子串。其时间复杂度为O()，因为需要遍历每个子串的起始和结束位置以填充 dp 数组，总共有 O()个状态；其空间复杂度也为O()，因为使用了 O() 的空间来存储 dp 数组，每个子串的回文状态都被记录下来。

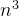
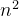
        思路三，暴力解法：遍历所有可能的子串，检查每个子串是否是回文。如果是回文且长度比当前最长的回文子串长，则更新结果。其时间复杂度：为O()，原因在于其遍历所有 O() 个子串，每个子串检查是否为回文需要 O(n)；其空间复杂度为O(1)，其只需要常数空间用于结果的存储。

        对比以上三种方法，中心扩展法在代码实现上最简洁，且具有较低的空间复杂度；动态规划法更适合理解和解决子串类的回文问题，但空间开销较大；暴力解法虽易于理解，但实际效率最低。

知识拓展：动态规划初了解

        动态规划（Dynamic Programming, DP）是一种算法设计技术，它用于解决具有重叠子问题和最优子结构特性的问题。动态规划通过将复杂问题分解为更简单的子问题，并存储这些子问题的解（通常是在表格中），从而避免重复计算，提高效率。以下是动态规划的几个关键点：

1. 重叠子问题：一个问题如果能分解为多个子问题，而这些子问题会重复出现多次，那么这个问题就具有重叠子问题的特性。动态规划通过存储这些子问题的解，使得每个子问题只解决一次。
2. 最优子结构：如果一个问题的最优解包含其子问题的最优解，那么这个问题就具有最优子结构特性。这意味着我们可以构建一个全局最优解，方法是将子问题的最优解组合起来。
3. 自底向上： 动态规划通常采用自底向上的方法，即从最小的子问题开始解决，逐步构建到原问题的解。
4. 状态转移方程：动态规划需要定义状态转移方程，它描述了如何从子问题的解构建出更大问题的解，而这也是动态规划的核心。

        动态规划通常被认为是以空间换取时间的典范，它通过存储中间结果，避免了在递归或迭代过程中对相同子问题的重复计算，能显著减少时间复杂度，尤其适用于那些具有明显递归结构的问题。

动态规划的基本思路

        以本题为例，探究动态规划的基本思路，建议配合上述代码详细查看：

1. 定义状态：

   • 我们定义一个二维布尔数组 dp[i][j]，表示子串 s[i:j+1] 是否是回文。
   • 如果 dp[i][j] == True，则 s[i:j+1] 是回文，否则不是。

2. 状态转移方程：

   • 一个字符串 s[i:j+1] 是回文，当且仅当：
     • s[i] == s[j]（子串的首尾字符相等），并且
     • s[i+1:j] 也是回文。

   • 因此，状态转移方程为： dp[i][j] = (s[i] == s[j]) and dp[i+1][j-1]

   • 特别地，对于回文的基本起点：
     • 如果子串长度为 1，即 i == j，那么 dp[i][j] = True，因为单个字符是回文。
     • 如果子串长度为 2，即 j = i + 1，只需判断 s[i] == s[j] 是否成立即可。

3. 初始化：

   • 对于所有单个字符 s[i:i+1]，dp[i][i] = True，因为单个字符是回文。
   • 对于所有长度为 2 的子串 s[i:i+2]，如果 s[i] == s[i+1]，则 dp[i][i+1] = True。

4. 计算顺序：

   • 我们需要从短到长计算子串的回文性，因为较长的子串依赖于较短的子串的状态。
   • 外层循环控制子串的长度 l，从 2 到 n（字符串长度）。
   • 内层循环控制子串的起始位置 i，计算 j = i + l - 1，并根据状态转移方程填充 dp[i][j]。

5. 结果：

   • 在填充 dp 数组的过程中，记录最长回文子串的起始位置和长度。
   • 最后，从字符串 s 中提取出最长的回文子串并返回。

感谢阅读，希望对你有所帮助~