【数据结构实战】二叉树——从根节点到叶节点

void HeapSort(int* a, int n)
{
	int i = 0;
	建堆--向上调整建堆
	//for (i = 0; i < n; i++)
	//{
	//	AdjustUp(a, i);
	//}
	
	//建堆--向下调整
	for (i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//排序
	for (i = 0; i < n; i++)
	{
		swap(&a[0], &a[n - i -1]);
		AdjustDown(a, n - i -1, 0);
	}
}

堆排序的时间复杂度为：O(n*logn)，已经比冒泡排序法（时间复杂度为：O(n^2)）快的很多很多啦

1.2 topk问题

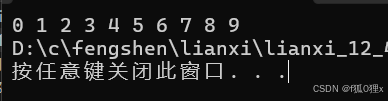
TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

例如给你1w个数据，选出其中最大的10个数字

这个问题的解决思路是：先将数据中的10个数据建小堆，然后再依次遍历剩下的数字，因为对顶的元素永远都是10个数中最小的元素，向下遍历的时候只有有数字比对顶元素大，就入堆，这样当所有数据遍历完的时候，这个堆里的数据，就是我们想要的数据

这里我们可以先在文件data.txt中先生成1w个小于1w的数据，然后我们再随机修改十个数字让他们大于1w，再然后用上述方法运行数据，如果打印出来的全是大于1w的就说明我们的思路没有问题

void PrintTopK(const char* file, int k)
{
	// 1. 建堆--用a中前k个元素建小堆
	int* topk = (int*)malloc(sizeof(int) * k);
	if (topk == NULL)
	{
		perror("PrintTopk::mslloc");
		return;
	}

	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}

	// 读出前k个数据建小堆
	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &topk[i]);
	}

	for (int i = (k - 2) / 2; i >= 0; --i)
	{
		AdjustDown(topk, k, i);
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	int val = 0;
	int ret = fscanf(fout, "%d", &val);
	while (ret != EOF)
	{
		if (val > topk[0])
		{
			topk[0] = val;
			AdjustDown(topk, k, 0);
		}

		ret = fscanf(fout, "%d", &val);
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", topk[i]);
	}
	printf("\n");

	free(topk);
	fclose(fout);
}

//造数据
void CreateNDate()
{
	int n = 10000;
	srand(time(NULL));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}
	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 10000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

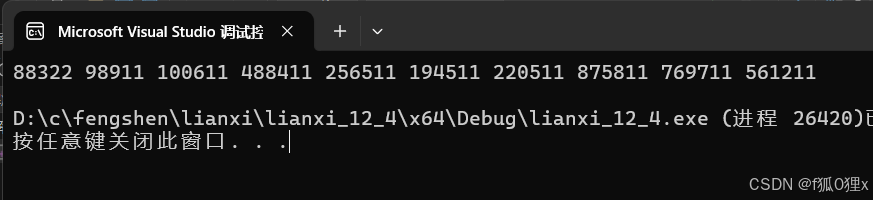
int main()
{
	CreateNDate();
	PrintTopK("data.txt", 10);
	return 0;
}

运行结果如下：

二、二叉树

2.1 二叉树链式结构的实现

这里我们就不像前面那几期一样讲他的增删查改啦，二叉树这个结构有更加巧妙的运用，所以我们就简单的手搓一个二叉树的链式结构出来

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* NewNode = (BTNode*)malloc(sizeof(BTNode));
	if (NewNode == NULL)
	{
		perror("BuyNode::malloc");
		return NULL;
	}
	NewNode->data = x;
	NewNode->left = NULL;
	NewNode->right = NULL;
	return NewNode;
}

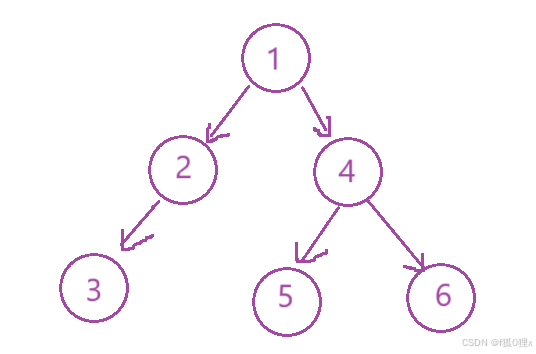
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

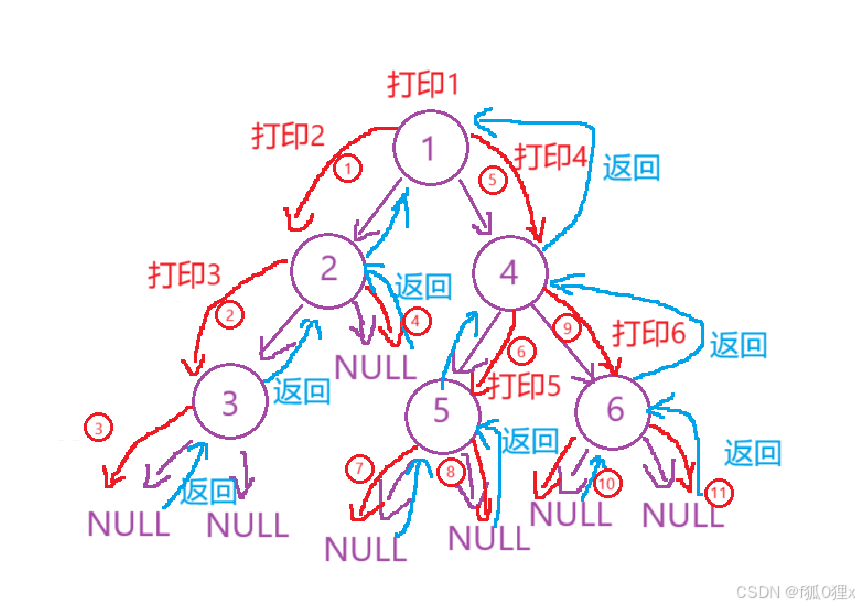
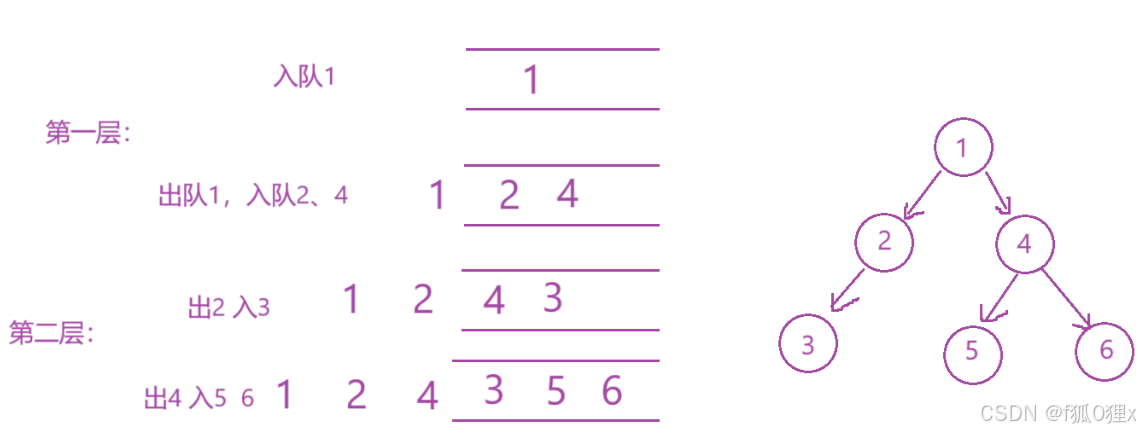
这样我们就把下图的二叉树的链式结构构造了出来：

2.2 二叉树的遍历

2.2.1 前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

我们随便观察一个二叉树，他都有根结点，左结点（可能为空）和右结点（可能为空），所以我们可以把遍历都看为这三个的不断递归

根据根结点的前后位置，分为了三种遍历方法：

前序：根结点、左结点、右结点
中序：左结点、根结点、右结点
后序：左结点、右结点、根节点

// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
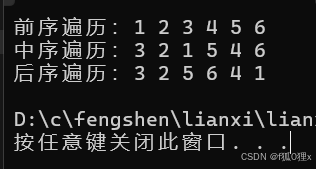
void PostOrder(BTNode* root);

我们先看前序遍历：

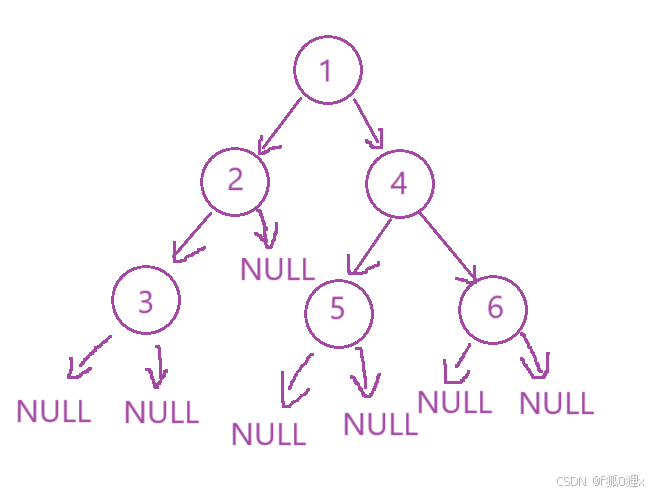
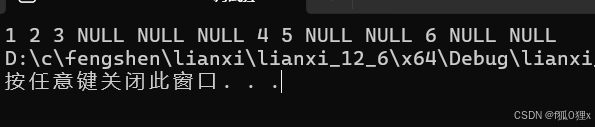
按照上述递归原理，我们就可以得到这样的顺序：

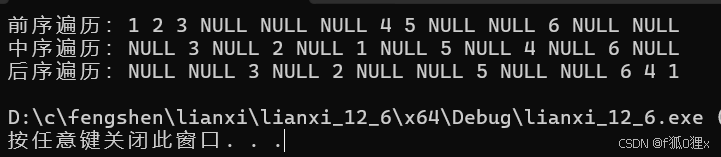
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL

（ps.图有点乱，我尽力了T﹏T）

代码如下：

// 二叉树前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);//根结点
	PreOrder(root->left);//左结点
	PreOrder(root->right);//右结点
}

同理，我们可以把中序遍历和后序遍历写出来：

中序：NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL

后序：：NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1

// 二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);//左结点
	printf("%d ", root->data);//根结点
	InOrder(root->right);//右结点
}
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);//左结点
	PostOrder(root->right);//右结点
	printf("%d ", root->data);//根结点
}

也可以不打印空结点：

2.2.2 层序遍历

层序遍历可以巧妙的运用到我们之前学的一个数据结构——队列

原理如下：

//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		QDatatype front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	QueueDestroy(&q);
}

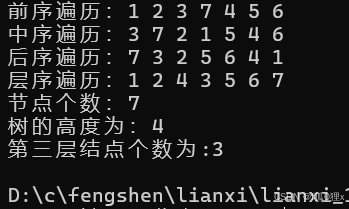
2.3 节点个数以及高度等

// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
//二叉树高度
int BinaryTreeHeight(BTNode* root);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

2.3.1 二叉树的结点个数

这里我们依然可以利用递归的想法，结点的个数就等于左边的子节点个数加右边的子节点个数再加上自己的1就可以啦

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

2.3.2 二叉树的第k层的结点个数

递归思路：当前第k层的结点个数 = 左子树第k-1层结点个数 + 右子树第k-1层结点个数

int TreeKLevel(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1) ;
}

2.3.3二叉树的高度

递归思路：当前节点的高度=左右孩子结点中高的那个的高度+1；

//二叉树高度
int BinaryTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int lheight = BinaryTreeHeight(root->left);
	int rheight = BinaryTreeHeight(root->right);
	return lheight > rheight ? lheight + 1 : rheight + 1;
}

2.3.4 二叉树查找值为x的节点

递归思想：找到就返回当前节点，没找到就继续从左子树和右子树开始找，直到根节点变为空结点返回

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	BTNode* left = BinaryTreeFind(root->left, x);
	if (left)
		return left;
	BTNode* right = BinaryTreeFind(root->right, x);
	if (right)
		return right;
	return NULL;
}

结语

感觉累了就对了，因为你正在走上坡路，本篇文章的难度较高，到这里就结束啦，下期我们将练习一下二叉树的OJ题来巩固学习一下，能看到这里的都是超级无敌帅气的小哥哥和美丽动人的小姐姐们，感谢你们能全篇看完，有啥疑问可以评论区或私信问我哈~

都看到这里啦~留下你的三连叭QAQ