一、3417. 跳过交替单元格的之字形遍历
题目链接
本题是一道模拟题,第一行走0,2,4,…偶数下标的格子,第二行走1,3,5,…奇数下标的格子(要倒着遍历),可以发现规律:
- 偶数行从前往后遍历偶数下标的格子
- 奇数行从后往前遍历奇数下标的格子
代码如下:
class Solution {
public List<Integer> zigzagTraversal(int[][] g) {
List<Integer> ans = new ArrayList<>();
boolean flg = false;
int n = g.length, m = g[0].length;
for(int i=0; i<g.length; i++){
if(!flg){
for(int j=0; j<m; j+=2){
ans.add(g[i][j]);
}
}else{
for(int j=m-1-m%2; j>=0; j-=2){
ans.add(g[i][j]);
}
}
flg = !flg;
}
return ans;
}
}
二、3418. 机器人可以获得的最大金币数
题目链接
定义
f
[
i
]
[
j
]
[
k
]
f[i][j][k]
f[i][j][k] : 从
(
0
,
0
)
(0,0)
(0,0) 到
(
i
,
j
)
(i,j)
(i,j) 且感化最多
k
k
k 个强盗可获得的最大金币数量。
选或不选
x
=
c
o
i
n
s
[
i
]
[
j
]
x = coins[i][j]
x=coins[i][j]:
- 不选 x x x,它只能从 ( i − 1 , j ) (i-1,j) (i−1,j) 和 ( i , j − 1 ) (i,j-1) (i,j−1) 转移过来,此时它的 k k k 也不会发生变化,即 f [ i ] [ j ] [ k ] = m a x ( f [ i − 1 ] [ j ] [ k ] , f [ i ] [ j − 1 ] [ k ] ) f[i][j][k]=max(f[i-1][j][k],f[i][j-1][k]) f[i][j][k]=max(f[i−1][j][k],f[i][j−1][k])
- 选择
x
x
x,它只能从
(
i
−
1
,
j
)
(i-1,j)
(i−1,j) 和
(
i
,
j
−
1
)
(i,j-1)
(i,j−1) 转移过来,此时它的
k
k
k 需要分情况讨论:
- i f ( k > 0 if(k > 0 if(k>0 && x < 0 ) x<0) x<0),此时可以感化当前单元格的强盗,即当前不获得也不损失金币,即 f [ i ] [ j ] [ k ] = m a x ( f [ i ] [ j ] [ k ] , f [ i − 1 ] [ j ] [ k − 1 ] , f [ i ] [ j − 1 ] [ k − 1 ] ) f[i][j][k]=max(f[i][j][k],f[i-1][j][k-1],f[i][j-1][k-1]) f[i][j][k]=max(f[i][j][k],f[i−1][j][k−1],f[i][j−1][k−1])
- 不使用感化能力次数 k k k,直接选 x x x,即 f [ i ] [ j ] [ k ] = m a x ( f [ i ] [ j ] [ k ] , f [ i − 1 ] [ j ] [ k − 1 ] + x , f [ i ] [ j − 1 ] [ k − 1 ] + x ) f[i][j][k]=max(f[i][j][k],f[i-1][j][k-1]+x,f[i][j-1][k-1]+x) f[i][j][k]=max(f[i][j][k],f[i−1][j][k−1]+x,f[i][j−1][k−1]+x)
PS:
- 这里 f [ i ] [ j ] f[i][j] f[i][j]是从 f [ i − 1 ] [ j ] f[i-1][j] f[i−1][j]和 f [ i ] [ j − 1 ] f[i][j-1] f[i][j−1]转移过来的,还需要注意越界访问,并且需要预处理第一行和第一列的值,所以在开数组的时候可以多开一行一列,此时递推公式就变成了 f [ i + 1 ] [ j + 1 ] = m a x ( f [ i + 1 ] [ j ] , f [ i ] [ j + 1 ] ) f[i+1][j+1] = max(f[i+1][j],f[i][j+1]) f[i+1][j+1]=max(f[i+1][j],f[i][j+1])。就不需要使用 i f if if 判断是否越界了
- 该题的答案可以为负值,所以需要在初始化的时候将所有位置置为 − i n f -inf −inf,除了 f [ 0 ] [ 1 ] [ k ] f[0][1][k] f[0][1][k] 和 f [ 1 ] [ 0 ] [ k ] f[1][0][k] f[1][0][k] ( k ∈ [ 0 , 2 ] ) (k\in [0,2]) (k∈[0,2]),因为 f [ 1 ] [ 1 ] [ k ] f[1][1][k] f[1][1][k] 即 ( 0 , 0 ) (0,0) (0,0)需要从上述两个状态转移过来,如果置为 − i n f -inf −inf,它在 ( 0 , 0 ) (0,0) (0,0)位置的值就变成了 − i n f -inf −inf,这显然不符合题意。
代码如下:
class Solution {
public int maximumAmount(int[][] coins) {
int n = coins.length, m = coins[0].length;
int[][][] f = new int[n+1][m+1][3];
//不选
//f[i][j][k] = max(f[i-1][j][k], f[i][j-1][k]);
//选
//f[i][j][k] = max(f[i-1][j][k], f[i][j-1][k]) + x
//if(k > 0 && x < 0)
//f[i][j][k] = max(f[i-1][j][k-1], f[i][j-1][k-1])
for(int[][] x : f){
for(int[] y : x){
Arrays.fill(y, Integer.MIN_VALUE/2);
}
}
Arrays.fill(f[0][1], 0);
//此时f[1][1][k]一定会从f[0][1][k]处转移过来,
//不会出现-inf这种情况,所以两个选一个赋值为0就行
//f[1][j>=1][k] 和 f[i>=1][1][k] 也是同理
//Arrays.fill(f[1][0], 0);
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
int x = coins[i][j];
for(int k=0; k<3; k++){
//不选的情况和选的第一种情况合起来
f[i+1][j+1][k] = Math.max(f[i+1][j][k], f[i][j+1][k]) + x;
if(k > 0 && x < 0)
f[i+1][j+1][k] = Math.max(f[i+1][j+1][k], Math.max(f[i+1][j][k-1], f[i][j+1][k-1]));
}
}
}
return f[n][m][2];
}
}
三、3419. 图的最大边权的最小值
题目链接
本题满足三个条件:
- 所有节点都能到达节点 0,反过来说,从节点 0 可以到所有节点,所以可以反向建图,通过 d f s ( 0 ) dfs(0) dfs(0) 计算可以到达的节点个数。
- 图中剩余边的最大边权值尽可能小,就是最大化最小值问题,可以使用二分来做。
- 每个节点至多有 t h r e s h o l d threshold threshold 条出去的边(即出度 ⩽ t h r e s h o l d \leqslant threshold ⩽threshold),这是个干扰条件,由于我们建立的是反图,这里的出度实际上是入度,而在 d f s ( 0 ) dfs(0) dfs(0) 遍历的时候,已经保证了所有点的入度为 1,题目也保证了 t h r e s h o l d ⩾ 1 threshold\geqslant1 threshold⩾1,所以只要能 d f s ( 0 ) dfs(0) dfs(0) 遍历到所有节点,这个条件就一定会满足!!!
代码如下:
class Solution {
public int minMaxWeight(int n, int[][] edges, int t) {
List<int[]>[] g = new ArrayList[n];
int mx = 0;
Arrays.setAll(g, e->new ArrayList<>());
for(int[] e : edges){
int x = e[0], y = e[1], w = e[2];
mx = Math.max(w, mx);
g[y].add(new int[]{x, w});
}
cnt = new int[n];
int l = 1, r = mx;
while(l <= r){
m = (l + r) / 2;
if(check(g)){
r = m - 1;
}else{
l = m + 1;
}
}
return r + 1 <= mx ? r + 1 : -1;
}
//由于每次二分的数字肯定不一样
//所以可以使用cnt[x] == m 来判断该点是否已经遍历过
int[] cnt;
int m;//当前二分的数字
boolean check(List<int[]>[] g){
int cnt = dfs(0, g);
return cnt == g.length;
}
int dfs(int x, List<int[]>[] g){
cnt[x] = m;
int res = 1;
for(int[] t : g[x]){
int y = t[0], w = t[1];
if(w <= m && cnt[y] != m){
res += dfs(y, g);
}
}
return res;
}
}
四、3420. 统计 K 次操作以内得到非递减子数组的数目
题目链接
本题求有多少满足条件的子数组(
k
k
k 次
+
1
+1
+1 操作内,使其变成非递减的子数组),可以使用滑动窗口,枚举右端点
r
r
r,维护左端点
l
l
l,设
c
n
t
cnt
cnt 为当前
[
l
,
r
]
[l,r]
[l,r] 的数组变成非递减所需的最少操作次数。如果
c
n
t
>
k
cnt > k
cnt>k,需要移动
l
l
l,直到
c
n
t
⩽
k
cnt\leqslant k
cnt⩽k,此时以
r
r
r 为右端点的满足条件的子数组有
r
−
l
+
1
r - l + 1
r−l+1。
本题的难点在于如何维护 c n t cnt cnt:
- 进窗口:将子数组变成非递减需要操作
t
=
m
a
x
(
0
,
m
a
x
(
n
u
m
s
[
l
:
r
]
)
−
n
u
m
s
[
r
]
)
t = max(0,max(nums[l:r])-nums[r])
t=max(0,max(nums[l:r])−nums[r]) ,
c
n
t
=
c
n
t
+
t
cnt = cnt + t
cnt=cnt+t,
- 如何维护区间
[
l
,
r
]
[l,r]
[l,r]最大值,可以使用单调队列 que(维护一个单调递减的序列)来维护。
- 如果 que.size() > 0 && \text{que.size() > 0 \&\&} que.size() > 0 && n u m s [ q u e . p e e k L a s t ( ) ] ⩽ n u m s [ r + 1 ] nums[que.peekLast()] \leqslant nums[r+1] nums[que.peekLast()]⩽nums[r+1] 时,说明 n u m s [ q u e . p e e k L a s t ( ) ] nums[que.peekLast()] nums[que.peekLast()] 不可能是当前区间的最大值了,直接删除 q u e . p o l l L a s t ( ) que.pollLast() que.pollLast(),把 r + 1 r+1 r+1添加进队列 q u e que que 中。
- 如果 q u e . p e e k F i r s t ( ) < l que.peekFirst() < l que.peekFirst()<l,说明该下标已经不在 [ l , r ] [l,r] [l,r]区间,直接删除 q u e . p o l l F i r s t ( ) que.pollFirst() que.pollFirst()。
- 区间 [ l , r ] [l,r] [l,r]的最大值为 n u m s [ q u e . p e e k F i r s t ( ) ] nums[que.peekFirst()] nums[que.peekFirst()]。
- 如何维护区间
[
l
,
r
]
[l,r]
[l,r]最大值,可以使用单调队列 que(维护一个单调递减的序列)来维护。
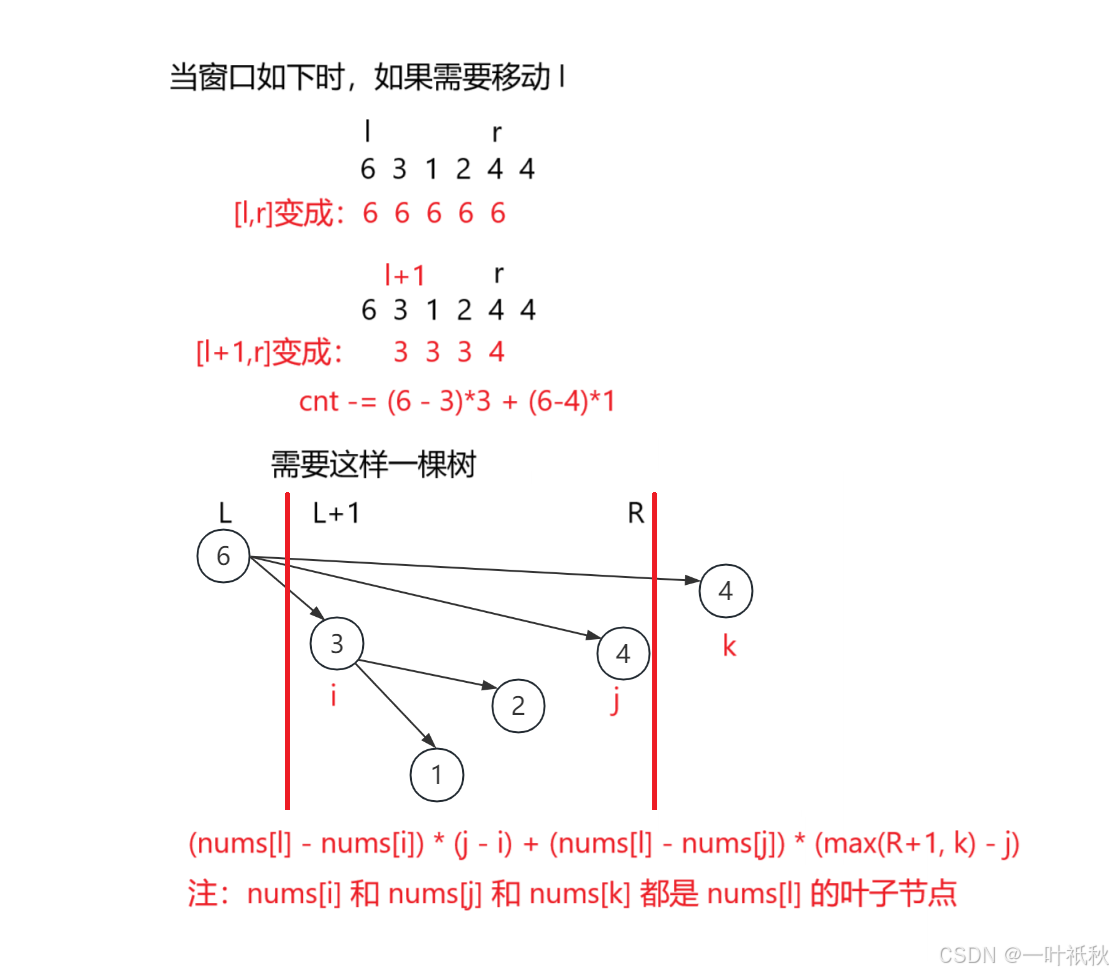
- 出窗口:
代码如下:
class Solution {
public long countNonDecreasingSubarrays(int[] nums, int k) {
int n = nums.length;
List<Integer>[] g = new ArrayList[n];
Arrays.setAll(g, e->new ArrayList<>());
Deque<Integer> st = new ArrayDeque<>();
int[] pos = new int[n];//记录右边第一个大于nums[i]的下标
Arrays.fill(pos, n);
for(int i=0; i<n; i++){
int v = nums[i];
while(st.size() > 0 && nums[st.peek()] <= v){
pos[st.pop()] = i;
}
if(st.size() > 0){
g[st.peek()].add(i);//构建上述所说的树
}
st.push(i);
}
int cnt = 0;
long ans = 0;
Deque<Integer> que = new ArrayDeque<>();
for(int l=0,r=0; r<n; r++){
int v = nums[r];
while(que.size() > 0 && nums[que.getLast()] <= v){
que.removeLast();
}
que.addLast(r);
cnt += Math.max(nums[que.getFirst()] - v, 0);
while(cnt > k){
int x = nums[l];
for(int i : g[l]){
if(i > r) break;
cnt -= (x - nums[i]) * (Math.min(pos[i], r+1)-i);
}
l++;
if(!que.isEmpty() && que.getFirst() < l)
que.removeFirst();
}
ans += r - l + 1;
}
return ans;
}
}