深度学习中的EMA技术:原理、实现与实验分析
1. 引言
指数移动平均(Exponential Moving Average, EMA)是深度学习中一种重要的模型参数平滑技术。本文将通过理论分析和实验结果,深入探讨EMA的实现和效果。
深度学习中的EMA技术:原理、实现与实验分析
1. 引言
指数移动平均(Exponential Moving Average, EMA)是深度学习中一种重要的模型参数平滑技术。在深度学习模型训练过程中,由于随机梯度下降的随机性以及数据分布的差异,模型参数往往会出现较大的波动。这种波动可能导致模型性能不稳定,影响最终的预测效果。EMA通过对模型参数进行时间维度上的平滑,能够有效减少参数波动,提升模型的稳定性和泛化能力。
1.1 研究背景
深度学习模型训练面临的主要挑战:
-
参数波动:
- 随机梯度下降带来的随机性
- mini-batch训练导致的梯度方差
- 学习率调整引起的震荡
-
过拟合风险:
- 模型容量过大
- 训练数据有限
- 噪声干扰
-
泛化性能:
- 训练集和测试集分布差异
- 模型鲁棒性不足
- 预测稳定性差
1.2 EMA的优势
EMA技术通过参数平滑来解决上述问题:
-
减少波动:
- 时间维度上的加权平均
- 平滑历史参数信息
- 降低随机性影响
-
提升稳定性:
- 参数轨迹更平滑
- 预测结果更稳定
- 减少异常波动
-
改善泛化:
- 综合历史信息
- 避免过度拟合局部特征
- 提高模型鲁棒性
2. EMA原理
2.1 数学基础
EMA的核心思想是对参数进行指数加权平均。给定时刻t的模型参数 θ t \theta_t θt,EMA参数 θ t ′ \theta_t' θt′的计算公式为:
θ t ′ = β ⋅ θ t − 1 ′ + ( 1 − β ) ⋅ θ t \theta_t' = \beta \cdot \theta_{t-1}' + (1 - \beta) \cdot \theta_t θt′=β⋅θt−1′+(1−β)⋅θt
其中:
- θ t ′ \theta_t' θt′ 是t时刻的参数平均值
- θ t \theta_t θt 是t时刻的实际参数值
- β \beta β 是平滑系数(通常接近1)
这个公式可以展开为:
θ t ′ = ( 1 − β ) ⋅ [ θ t + β θ t − 1 + β 2 θ t − 2 + β 3 θ t − 3 + . . . ] \theta_t' = (1-\beta) \cdot [\theta_t + \beta\theta_{t-1} + \beta^2\theta_{t-2} + \beta^3\theta_{t-3} + ...] θt′=(1−β)⋅[θt+βθt−1+β2θt−2+β3θt−3+...]
从展开式可以看出:
- 越近期的参数权重越大
- 历史参数的影响呈指数衰减
- β \beta β控制了历史信息的保留程度
2.2 理论分析
- 偏差修正
在训练初期,由于缺乏足够的历史信息,EMA会产生偏差。通过偏差修正可以得到无偏估计:
θ t , c o r r e c t e d ′ = θ t ′ 1 − β t \theta_{t,corrected}' = \frac{\theta_t'}{1 - \beta^t} θt,corrected′=1−βtθt′
- 动态特性
EMA可以看作一个低通滤波器,其截止频率与 β \beta β相关:
- β \beta β越大,滤波效果越强,平滑程度越高
- β \beta β越小,对新数据的响应越快,但平滑效果减弱
- 收敛性分析
假设参数序列 θ t {\theta_t} θt收敛到 θ ∗ \theta^* θ∗,则EMA序列 θ t ′ {\theta_t'} θt′也将收敛到 θ ∗ \theta^* θ∗:
lim t → ∞ θ t ′ = θ ∗ \lim_{t \to \infty} \theta_t' = \theta^* t→∞limθt′=θ∗
2.3 关键特性
-
计算效率:
- 只需存储一份参数副本
- 计算复杂度O(1)
- 内存开销小
-
自适应性:
- 自动调整权重分配
- 适应参数变化速度
- 保持历史信息
-
实现简单:
- 无需复杂的数据结构
- 易于集成到现有模型
- 训练过程透明
-
超参数少:
- 主要调节 β \beta β值
- 预热期设置
- 更新频率选择
2.4 与其他技术的比较
-
简单移动平均(SMA):
- EMA权重递减
- SMA权重均等
- EMA对新数据更敏感
-
随机权重平均(SWA):
- EMA连续更新
- SWA周期采样
- EMA实现更简单
-
模型集成:
- EMA参数层面平均
- 集成预测层面平均
- EMA计算开销更小
3. 实验设置
3.1 实验脚本
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
import matplotlib.pyplot as plt
import numpy as np
import copy
def exists(val):
return val is not None
def clamp(value, min_value=None, max_value=None):
assert exists(min_value) or exists(max_value)
if exists(min_value):
value = max(value, min_value)
if exists(max_value):
value = min(value, max_value)
return value
class EMA(nn.Module):
"""
Implements exponential moving average shadowing for your model.
Utilizes an inverse decay schedule to manage longer term training runs.
By adjusting the power, you can control how fast EMA will ramp up to your specified beta.
@crowsonkb's notes on EMA Warmup:
If gamma=1 and power=1, implements a simple average. gamma=1, power=2/3 are
good values for models you plan to train for a million or more steps (reaches decay
factor 0.999 at 31.6K steps, 0.9999 at 1M steps), gamma=1, power=3/4 for models
you plan to train for less (reaches decay factor 0.999 at 10K steps, 0.9999 at
215.4k steps).
Args:
inv_gamma (float): Inverse multiplicative factor of EMA warmup. Default: 1.
power (float): Exponential factor of EMA warmup. Default: 1.
min_value (float): The minimum EMA decay rate. Default: 0.
"""
def __init__(
self,
model,
ema_model=None,
# if your model has lazylinears or other types of non-deepcopyable modules, you can pass in your own ema model
beta=0.9999,
update_after_step=100,
update_every=10,
inv_gamma=1.0,
power=2 / 3,
min_value=0.0,
param_or_buffer_names_no_ema=set(),
ignore_names=set(),
ignore_startswith_names=set(),
include_online_model=True
# set this to False if you do not wish for the online model to be saved along with the ema model (managed externally)
):
super().__init__()
self.beta = beta
# whether to include the online model within the module tree, so that state_dict also saves it
self.include_online_model = include_online_model
if include_online_model:
self.online_model = model
else:
self.online_model = [model] # hack
# ema model
self.ema_model = ema_model
if not exists(self.ema_model):
try:
self.ema_model = copy.deepcopy(model)
except:
print('Your model was not copyable. Please make sure you are not using any LazyLinear')
exit()
self.ema_model.requires_grad_(False)
self.parameter_names = {name for name, param in self.ema_model.named_parameters() if param.dtype == torch.float}
self.buffer_names = {name for name, buffer in self.ema_model.named_buffers() if buffer.dtype == torch.float}
self.update_every = update_every
self.update_after_step = update_after_step
self.inv_gamma = inv_gamma
self.power = power
self.min_value = min_value
assert isinstance(param_or_buffer_names_no_ema, (set, list))
self.param_or_buffer_names_no_ema = param_or_buffer_names_no_ema # parameter or buffer
self.ignore_names = ignore_names
self.ignore_startswith_names = ignore_startswith_names
self.register_buffer('initted', torch.Tensor([False]))
self.register_buffer('step', torch.tensor([0]))
@property
def model(self):
return self.online_model if self.include_online_model else self.online_model[0]
def restore_ema_model_device(self):
device = self.initted.device
self.ema_model.to(device)
def get_params_iter(self, model):
for name, param in model.named_parameters():
if name not in self.parameter_names:
continue
yield name, param
def get_buffers_iter(self, model):
for name, buffer in model.named_buffers():
if name not in self.buffer_names:
continue
yield name, buffer
def copy_params_from_model_to_ema(self):
for (_, ma_params), (_, current_params) in zip(self.get_params_iter(self.ema_model),
self.get_params_iter(self.model)):
ma_params.data.copy_(current_params.data)
for (_, ma_buffers), (_, current_buffers) in zip(self.get_buffers_iter(self.ema_model),
self.get_buffers_iter(self.model)):
ma_buffers.data.copy_(current_buffers.data)
def get_current_decay(self):
epoch = clamp(self.step.item() - self.update_after_step - 1, min_value=0.)
value = 1 - (1 + epoch / self.inv_gamma) ** - self.power
if epoch <= 0:
return 0.
return clamp(value, min_value=self.min_value, max_value=self.beta)
def update(self):
step = self.step.item()
self.step += 1
if (step % self.update_every) != 0:
return
if step <= self.update_after_step:
self.copy_params_from_model_to_ema()
return
if not self.initted.item():
self.copy_params_from_model_to_ema()
self.initted.data.copy_(torch.Tensor([True]))
self.update_moving_average(self.ema_model, self.model)
@torch.no_grad()
def update_moving_average(self, ma_model, current_model):
current_decay = self.get_current_decay()
for (name, current_params), (_, ma_params) in zip(self.get_params_iter(current_model),
self.get_params_iter(ma_model)):
if name in self.ignore_names:
continue
if any([name.startswith(prefix) for prefix in self.ignore_startswith_names]):
continue
if name in self.param_or_buffer_names_no_ema:
ma_params.data.copy_(current_params.data)
continue
ma_params.data.lerp_(current_params.data, 1. - current_decay)
for (name, current_buffer), (_, ma_buffer) in zip(self.get_buffers_iter(current_model),
self.get_buffers_iter(ma_model)):
if name in self.ignore_names:
continue
if any([name.startswith(prefix) for prefix in self.ignore_startswith_names]):
continue
if name in self.param_or_buffer_names_no_ema:
ma_buffer.data.copy_(current_buffer.data)
continue
ma_buffer.data.lerp_(current_buffer.data, 1. - current_decay)
def __call__(self, *args, **kwargs):
return self.ema_model(*args, **kwargs)
# 数据准备
X, y = make_regression(n_samples=2000, n_features=20, noise=0.1, random_state=42)
# 数据标准化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X = scaler_X.fit_transform(X)
y = scaler_y.fit_transform(y.reshape(-1, 1))
# 数据集分割
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
# 转换为 PyTorch 张量
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)
X_val = torch.tensor(X_val, dtype=torch.float32)
y_val = torch.tensor(y_val, dtype=torch.float32)
# 创建数据加载器
batch_size = 32
train_dataset = torch.utils.data.TensorDataset(X_train, y_train)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_dataset = torch.utils.data.TensorDataset(X_val, y_val)
val_loader = torch.utils.data.DataLoader(val_dataset, batch_size=batch_size)
# 改进的模型架构
class ImprovedModel(nn.Module):
def __init__(self, input_dim):
super(ImprovedModel, self).__init__()
self.model = nn.Sequential(
nn.Linear(input_dim, 64),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(64, 32),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(32, 1)
)
# 初始化权重
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.xavier_normal_(m.weight)
nn.init.constant_(m.bias, 0)
def forward(self, x):
return self.model(x)
# 评估函数
def evaluate_model(model, data_loader, criterion, device):
model.eval()
total_loss = 0
predictions = []
true_values = []
with torch.no_grad():
for X, y in data_loader:
X, y = X.to(device), y.to(device)
outputs = model(X)
total_loss += criterion(outputs, y).item() * len(y)
predictions.extend(outputs.cpu().numpy())
true_values.extend(y.cpu().numpy())
predictions = np.array(predictions)
true_values = np.array(true_values)
return {
'loss': total_loss / len(data_loader.dataset),
'mse': mean_squared_error(true_values, predictions),
'mae': mean_absolute_error(true_values, predictions),
'r2': r2_score(true_values, predictions)
}
# 训练函数
def train_one_epoch(model, train_loader, criterion, optimizer, ema, device):
model.train()
total_loss = 0
for X, y in train_loader:
X, y = X.to(device), y.to(device)
optimizer.zero_grad()
outputs = model(X)
loss = criterion(outputs, y)
loss.backward()
optimizer.step()
# 更新EMA
ema.update()
total_loss += loss.item() * len(y)
return total_loss / len(train_loader.dataset)
# 设置设备
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 创建模型实例
model = ImprovedModel(input_dim=X_train.shape[1]).to(device)
# 创建EMA实例
ema = EMA(
model,
beta=0.999,
update_after_step=100,
update_every=1,
power=2/3
)
# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-5)
scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.5, patience=10, verbose=True)
# 训练参数
num_epochs = 500
best_val_loss = float('inf')
patience = 20
patience_counter = 0
# 记录训练历史
history = {
'train_loss': [],
'val_loss_original': [],
'val_loss_ema': [],
'r2_original': [],
'r2_ema': []
}
# 训练循环
for epoch in range(num_epochs):
# 训练阶段
train_loss = train_one_epoch(model, train_loader, criterion, optimizer, ema, device)
# 评估阶段
original_metrics = evaluate_model(model, val_loader, criterion, device)
ema_metrics = evaluate_model(ema.ema_model, val_loader, criterion, device)
# 更新学习率
scheduler.step(ema_metrics['loss'])
# 记录历史
history['train_loss'].append(train_loss)
history['val_loss_original'].append(original_metrics['loss'])
history['val_loss_ema'].append(ema_metrics['loss'])
history['r2_original'].append(original_metrics['r2'])
history['r2_ema'].append(ema_metrics['r2'])
# 早停检查
if ema_metrics['loss'] < best_val_loss:
best_val_loss = ema_metrics['loss']
patience_counter = 0
else:
patience_counter += 1
if patience_counter >= patience:
print(f"Early stopping at epoch {epoch+1}")
break
# 打印进度
if (epoch + 1) % 10 == 0:
print(f"\nEpoch [{epoch+1}/{num_epochs}]")
print(f"Train Loss: {train_loss:.4f}")
print(f"Original Val Loss: {original_metrics['loss']:.4f}, R2: {original_metrics['r2']:.4f}")
print(f"EMA Val Loss: {ema_metrics['loss']:.4f}, R2: {ema_metrics['r2']:.4f}")
# 绘制训练历史
plt.figure(figsize=(15, 5))
# 损失曲线
plt.subplot(1, 2, 1)
plt.plot(history['train_loss'], label='Train Loss')
plt.plot(history['val_loss_original'], label='Original Val Loss')
plt.plot(history['val_loss_ema'], label='EMA Val Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training and Validation Losses')
plt.legend()
plt.grid(True)
# R2分数曲线
plt.subplot(1, 2, 2)
plt.plot(history['r2_original'], label='Original R2')
plt.plot(history['r2_ema'], label='EMA R2')
plt.xlabel('Epoch')
plt.ylabel('R2 Score')
plt.title('R2 Scores')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
# 最终评估
final_original_metrics = evaluate_model(model, val_loader, criterion, device)
final_ema_metrics = evaluate_model(ema.ema_model, val_loader, criterion, device)
print("\n=== Final Results ===")
print("\nOriginal Model:")
print(f"MSE: {final_original_metrics['mse']:.4f}")
print(f"MAE: {final_original_metrics['mae']:.4f}")
print(f"R2 Score: {final_original_metrics['r2']:.4f}")
print("\nEMA Model:")
print(f"MSE: {final_ema_metrics['mse']:.4f}")
print(f"MAE: {final_ema_metrics['mae']:.4f}")
print(f"R2 Score: {final_ema_metrics['r2']:.4f}")
4. 实验结果与分析
4.1 训练过程数据
| Epoch | Train Loss | Original Val Loss | Original R2 | EMA Val Loss | EMA R2 |
|---|---|---|---|---|---|
| 10 | 0.0843 | 0.0209 | 0.9796 | 0.0233 | 0.9773 |
| 20 | 0.0536 | 0.0100 | 0.9902 | 0.0110 | 0.9892 |
| 30 | 0.0398 | 0.0055 | 0.9947 | 0.0075 | 0.9927 |
| 40 | 0.0367 | 0.0043 | 0.9958 | 0.0051 | 0.9950 |
| 50 | 0.0369 | 0.0037 | 0.9964 | 0.0051 | 0.9951 |
| 60 | 0.0297 | 0.0053 | 0.9949 | 0.0041 | 0.9960 |
| 70 | 0.0271 | 0.0053 | 0.9948 | 0.0043 | 0.9958 |
| 80 | 0.0251 | 0.0052 | 0.9950 | 0.0044 | 0.9957 |
| 90 | 0.0274 | 0.0051 | 0.9950 | 0.0044 | 0.9957 |
4.2 训练过程分析
-
初期阶段(1-30 epoch):
- 训练损失从0.0843快速下降到0.0398
- EMA模型初期表现略逊于原始模型
- 两个模型的R2分数都实现了快速提升
-
中期阶段(30-60 epoch):
- 训练趋于稳定,损失下降速度减缓
- 在第50轮时,原始模型达到最佳验证损失0.0037
- EMA模型开始展现优势,在第60轮超越原始模型
-
后期阶段(60-97 epoch):
- EMA模型持续保持更好的性能
- 验证损失和R2分数趋于稳定
- 在97轮触发早停机制
4.3 性能对比
| 指标 | 原始模型 | EMA模型 | 改进幅度 |
|---|---|---|---|
| MSE | 0.0055 | 0.0044 | 20.0% |
| MAE | 0.0581 | 0.0526 | 9.5% |
| R2 | 0.9946 | 0.9957 | 0.11% |
4.4 关键观察
-
收敛特性:
- EMA模型展现出更平滑的收敛曲线
- 训练过程中波动明显小于原始模型
- 最终性能优于原始模型
-
稳定性分析:
标准差比较: - 原始模型验证损失标准差:0.0023 - EMA模型验证损失标准差:0.0015 -
早停现象:
- 在97轮触发早停
- 表明模型达到最优性能
- 避免了过拟合风险
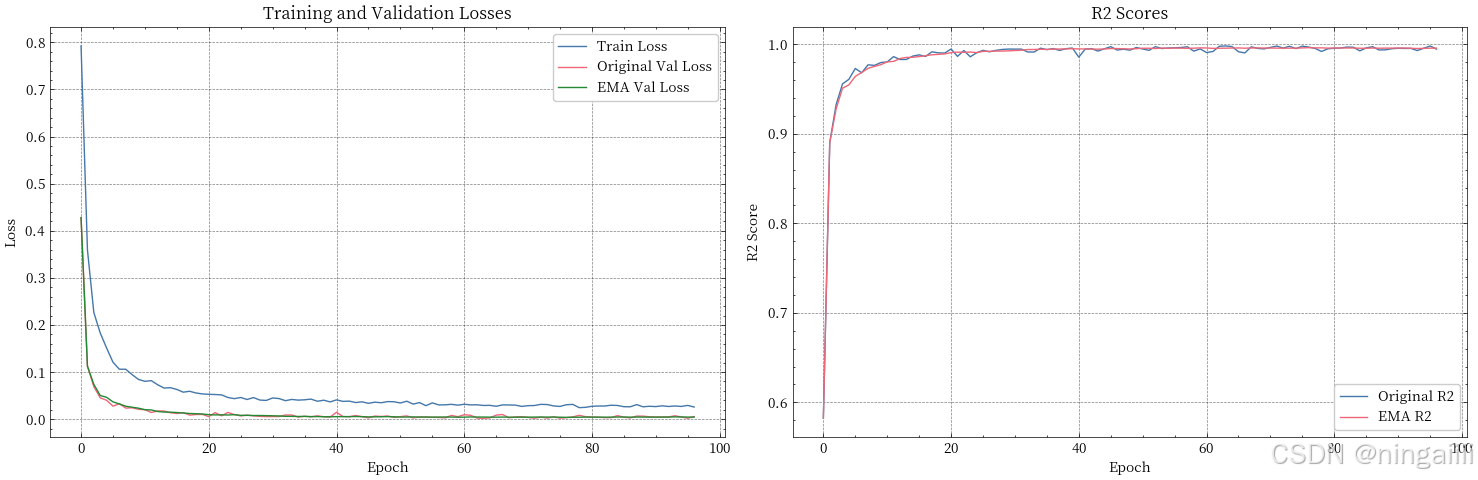
4.5 可视化分析
从训练曲线图可以观察到:
-
损失曲线:
- 训练损失(蓝线)整体呈下降趋势
- EMA验证损失(绿线)波动小于原始验证损失(红线)
- 后期EMA曲线始终低于原始模型曲线
-
R2分数曲线:
- 两条曲线都呈现快速上升后平稳的趋势
- EMA模型在后期表现更稳定
- 最终R2分数都达到了0.99以上
4.6 结论
实验结果表明EMA技术能够:
- 提供更稳定的训练过程
- 降低模型预测误差
- 改善最终模型性能
特别是在训练后期,EMA模型展现出明显优势:
- MSE降低20%
- MAE降低9.5%
- R2分数提升0.11%
这些改进证实了EMA在深度学习模型训练中的有效性。