在你没有全力以赴之前，都不要抱怨环境，等你努力做到极限了再说

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]

输出：6

解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]

输出：9

提示：

n == height.length

1 <= n <= 2 * 104

0 <= height[i] <= 105

思路分析

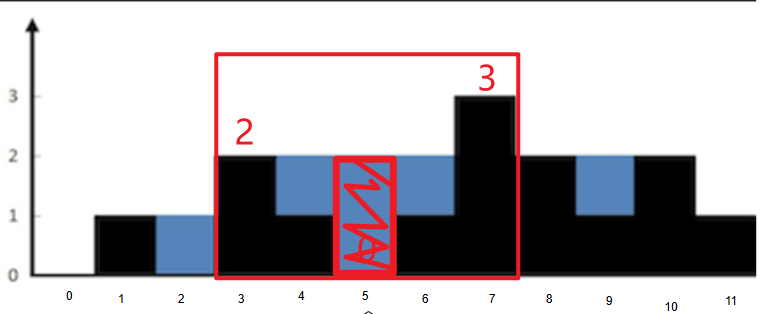
• 思考每一个位置能接多少雨水，比如位置5，他的水量是2，2是怎么来的呢？

• 答：从5号位置向左找最大高度，显然为2，向右找最大高度，显然为3，由于短板效应，水必然会从木板短的流走，故取min(left_max,right_max),然后再减去自己的高度，就是盛水量即min(2,3)-0=2

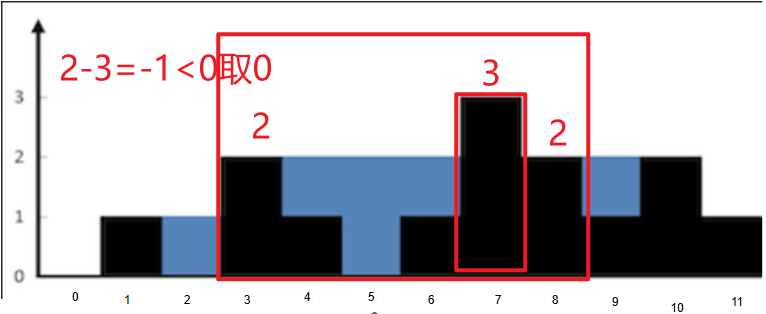
• 抽象出来就是 i位置的当前水量=min(left_max,right_max)-height[i]

• 注意：如果min(left_max,right_max)-height[i]这个数值小于0，那么取0，可能i位置没有水，但不会为负数，如下图所示。

• 接下来，问题就转化为每一个位置的left_max,和right_max如何求？

• 答：使用两个辅助数组，记录下每个位置i， left_max[i] 从 height[0] 到 height[i] 的最大值和 right_max[i] 从 height[i] 到 height[n-1] 的最大值

• 时间复杂度O(n), 空间复杂度O(n)

• 在此基础上可以继续优化，使用双指针，不需要辅助数组，做到空间复杂度O(1)

• 使用有限几个变量，l,r,left_max,right_max

• 使用双指针，配合了单调性分析，增加了左侧部分最大值，和右边部分最大值，left_max和right_max谁是小的一旦暴漏，就可以结算那一侧当前的水量。此时就优化了之前的辅助数组。

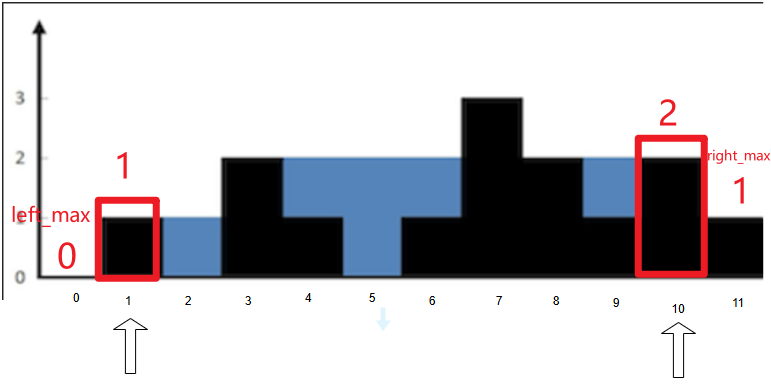
• 举个例子

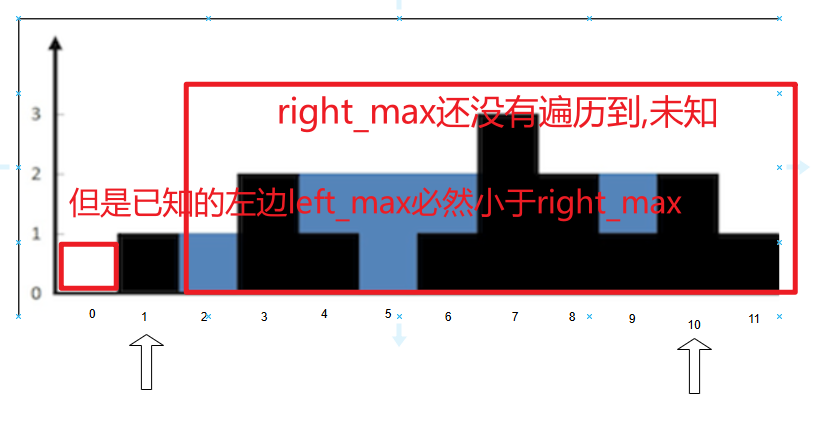
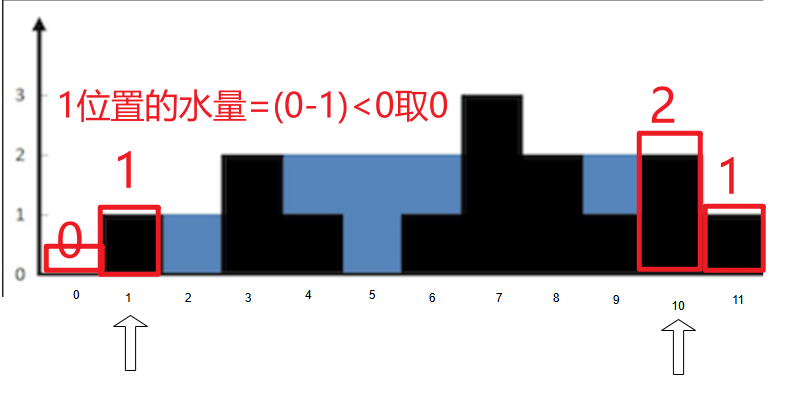
• 由于0位置的left_max<11位置的right_max,那么左侧位置的l就可以结算答案了，为min(0,1)-1=-1,所以取水量0

• 为什么呢？因为1位置的水量是由min(left_max,right_max)决定的，而左侧部分的最大值已经出现了，故可以结算答案

完整代码

//未优化版本
class Solution {
public:
    int trap(vector<int>& height) {
        //i位置的雨水==min(左max，右max)-height[i]
        //由于短板效应，水会从较为小的那一边流淌出去
        //注：如果减出来是负数，说明没有水
        // 使用辅助空间pre_max,suf_max
        // 0-i范围上的最大值，记录在lmax[i]
        int n=height.size();
        vector<int>pre_max(n);
        vector<int>suf_max(n);
        pre_max[0]=height[0];
        suf_max[n-1]=height[n-1];
        for(int i=1;i<n;i++){
            pre_max[i]=max(pre_max[i-1],height[i]);
        }
        for(int i=n-2;i>=0;i--){
            suf_max[i]=max(suf_max[i+1],height[i]);
        }
        int ans=0;
        for(int i=0;i<n;i++){
            int tmp=min(pre_max[i],suf_max[i])-height[i];
            if(tmp>0){
                ans+=tmp;
            }
        }
        return ans;

    }
};



//优化版本
class Solution {
public:
    int trap(vector<int>& nums) {
        int l = 1;//0位置是没有水量的
        int r = nums.size() - 1;//最后一个位置是没有水量的，故初始化为倒二
        int lmax = nums[0];//第一个位置
        int rmax = nums[nums.size() - 1];//最后一个位置
        int ans=0;
        while (l <= r) {
            //谁一旦暴漏，就是小，就可以结算哪一侧的答案
            if (lmax <= rmax) {
                ans += max(0, lmax - nums[l]);//结算左侧答案
                lmax = max(lmax, nums[l++]);//更新左侧最大值
            }else{
                ans += max(0, rmax - nums[r]);//结算右侧答案
                rmax = max(rmax, nums[r--]);//更新右侧最大值
            }
        }
        return ans;
    }
};