目录
一、数据结构
数据结构包括:数组、栈、队列、字符串、链表、树、图、堆、哈希表等。
线性表结构:线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。
非线性表结构:与线性表结构相对立的概念是非线性表结构。比如二叉树、堆、图等。之所以叫非线性,是因为,在非线性表中,数据之间并不是简单的前后关系。
1、堆
(1)、认识堆
js 中引用类型的变量是存放在堆中的。
堆通常是一个可以被看做一棵树(完全二叉树)的数组对象。
堆是非线性数据结构,相当于一维数组,有两个直接后继。
堆总是满足下列性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。
栈是先进后出的,但是于堆而言却没有这个特性,两者都是存放临时数据的地方。 对于堆,我们可以随心所欲的进行增加变量和删除变量,不要遵循什么次序,只要你喜欢。
堆(Heap)是应用程序在运行的时候请求操作系统分配给自己内存(堆是在程序运行时,而不是在程序编译时,申请某个大小的内存空间)。即动态分配内存,对其访问和对一般内存的访问没有区别——堆是指程序运行是申请的动态内存,而栈只是指一种使用堆的方法(即先进后出)。
堆存放在二级缓存中,生命周期由虚拟机的垃圾回收算法来决定(并不是一旦成为孤儿对象就能被回收)。因此调用这些对象的速度要相对来得低一些。
堆的优势:可以动态地分配内存大小,生存期也不必事先告诉编译器。
堆的缺点:由于要在运行时动态分配内存,存取速度较慢。
(2)、堆的应用
- 根据字符出现频率排序
- 超级丑数
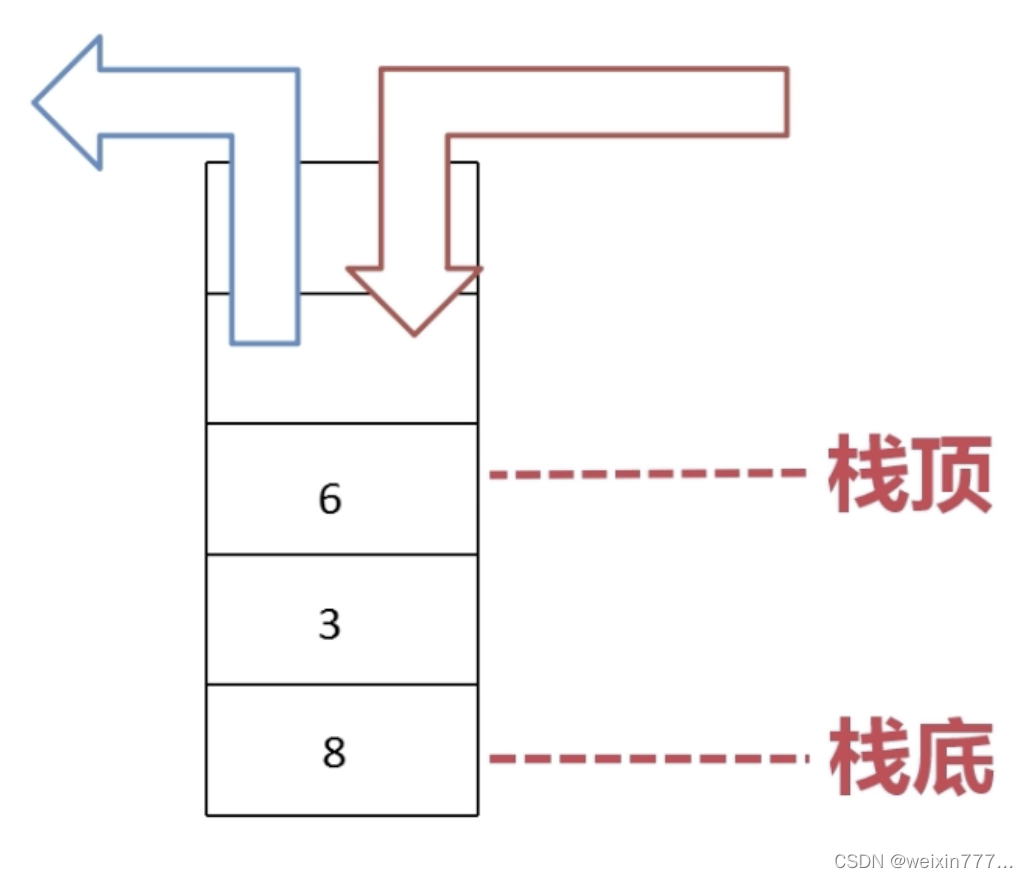
2、栈
(1)、认识栈
js 中基本类型的变量是存放在栈中的。
栈又名堆栈,是一种后进先出(FIFO)的数据结构。
栈是一种运算受限的线性表(限定仅在栈顶进行插入和删除操作)。
栈存放在一级缓存中, 他们通常都是被调用时处于存储空间中,调用完毕立即释放。
栈的优势:存取速度比堆要快。
栈的缺点:存在栈中的数据大小与生存期必须是确定的,缺乏灵活性。
(2)、栈的应用
- 棒球比赛
- 最大矩形
3、队列
(1)、认识队列
队列是一种先进先出(FIFO)的数据结构。
队列是一种运算受限的线性表(它只允许在表的前端进行删除操作,在表的后端进行插入操作)。
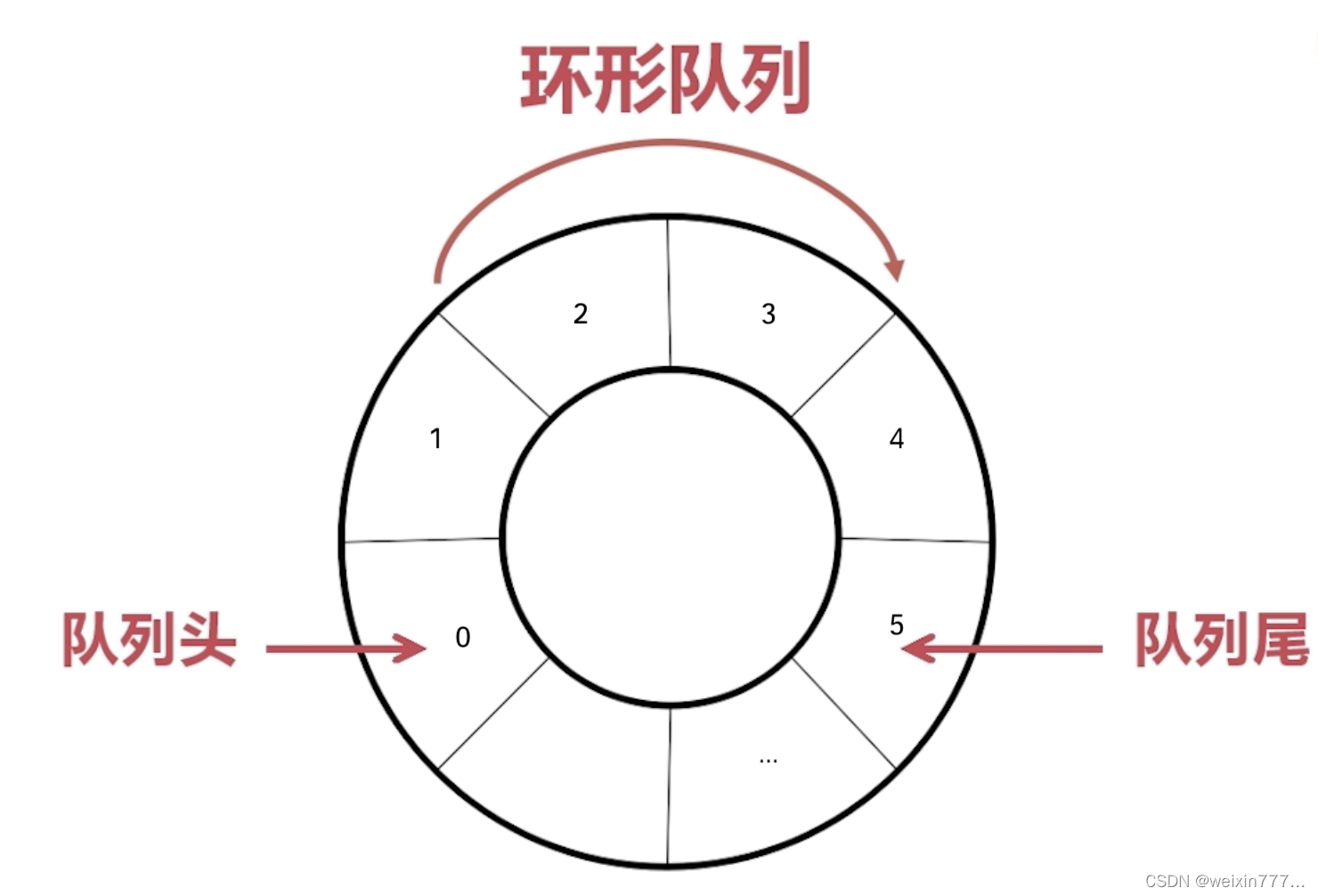
队列分为 顺序队列(下左图) 和 循环队列(下右图)。
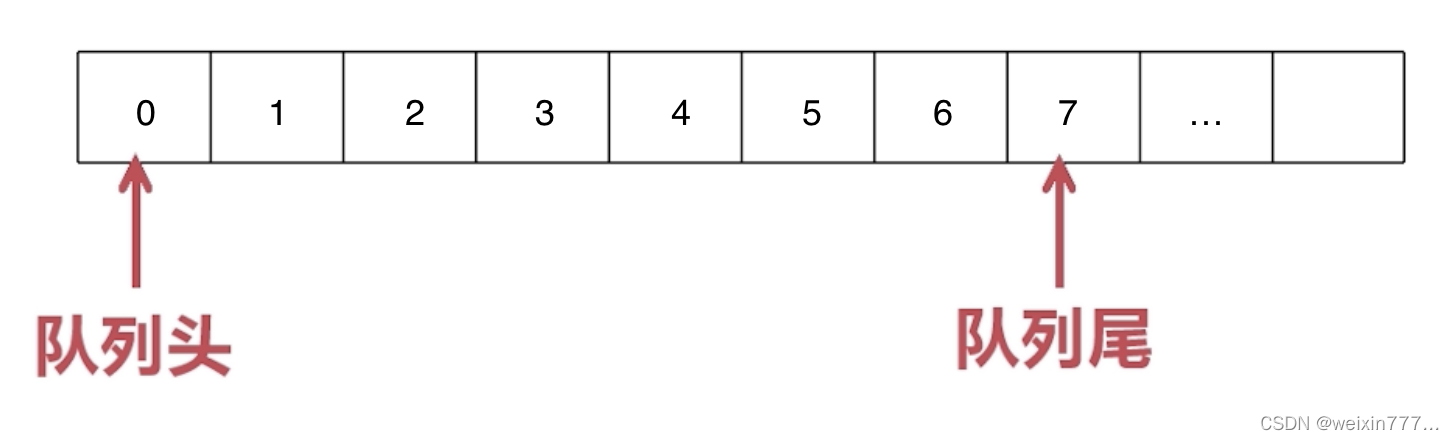
顺序队列中的溢出现象:
- "下溢"现象:当队列为空时,做出队运算产生的溢出现象。“下溢”是正常现象,常用作程序控制转移的条件。
- "真上溢"现象:当队列满时,做进栈运算产生空间溢出的现象。“真上溢”是一种出错状态,应设法避免。
- "假上溢"现象:由于入队和出队操作中,头尾指针只增加不减小,致使被删元素的空间永远无法重新利用。当队列中实际的元素个数远远小于向量空间的规模时,也可能由于尾指针已超越向量空间的上界而不能做入队操作。该现象称为"假上溢"现象。
(2)、队列的应用
- 设计循环队列
- 任务调度器
4、链表
(1)、认识链表
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。
链表有很多种不同的类型:单向链表,双向链表以及循环链表。
链表的优势:
- 不需要预先知道数据大小。
- 常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序,数据的存取往往要在不同的排列顺序中转换。链表允许插入和移除表上任意位置上的节点,但是不允许随机存取。
- 由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
链表的缺点:
- 链表失去了数组随机读取的优点。
- 链表由于增加了结点的指针域,空间开销比较大。
【链表VS数组】
JS 中的数组没有固定的长度。这相较于很多其他的编程语言是非常方便的,因为很多其他编程语言的数组长度是固定的,当达到数组的最大长度以后再想向其中添加数据是非常麻烦的,且使用数组的时候添加和删除元素和变得非常的困难。
JS 中的数组异常灵活。push + pop 组合可以构建出一个堆栈,push + shift 组合可以构建出一个队列等等。
既然 JS 的数组有那么多的优点,为什么还需要 “链表” 这个数据结构呢?
因为:JS 中的数组主要的问题是被实现成了对象,和其他语言的数组相比效率很低。链表除了不能随机访问之外,几乎可以用在任何可以使用 “一维数组” 的情况中。
(2)、链表的实现
链表中的节点类型描述如下:
class Node {
constructor(data) {
this.data = data; // 节点的数据域
this.prev = null; // 节点的指针域
this.next = null; // 节点的指针域
}
}- 双向链表:会有 prev 和 next 两个指针域;
- 单链表:只有 next 指针。
(3)、单链表数据结构的大概框架
class SingleList {
constructor() {
this.size = 0; // 单链表的长度
this.head = new Node('head'); // 表头节点
this.currNode = ''; // 当前节点的指向
}
find(item) {} // 在单链表中寻找item元素
insert(item, element) {} // 向单链表中插入元素
remove(item) {} // 在单链表中删除一个节点
append(element) {} // 在单链表的尾部添加元素
findLast() {} // 获取单链表的最后一个节点
isEmpty() {} // 判断单链表是否为空
show() {} // 显示当前节点
getLength() {} // 获取单链表的长度
advance(n, currNode) {} // 从当前节点向前移动n个位置
display() {} // 单链表的遍历显示
clear() {} // 清空单链表
}从上述代码可以看到:该单链表是使用带有表头节点的形式来实现的。下面是对其稍微复杂的方法进行实现。
1⃣️、在单链表中寻找item元素
find(item) {
let currNode = this.head;
while (currNode && (currNode.data !== item)) {
currNode = currNode.next;
}
return currNode;
}2⃣️、只要当前节点的next指针不为空就一直向下遍历,直到当前节点的next为空时即是最后一个节点了。
findLast() {
let currNode = this.head;
while (currNode.next) {
currNode = currNode.next;
}
return currNode;
}3⃣️、从当前位置向前移动 n 个节点
advance(n, currNode = this.head) {
this.currNode = currNode;
while ((n--) && this.currNode.next) {
this.currNode = this.currNode.next;
}
return this.currNode;
}
注意advance()函数中的currNode参数使用了默认的this.head。当向前移动的位数超过单链表的长度时,总是返回单链表的最后一个节点。
4⃣️、在尾部添加元素
append(element) {
let newNode = new Node(element);
let currNode = this.findLast();
currNode.next = newNode;
this.size++;
}在尾部添加元素时使用到了findLast()方法,findLast()方法返回单链表的最后一个元素,因此在单链表的尾部添加元素时,只要将新元素赋值给单链表的最后一个元素的next指针即可。
5⃣️、向单链表中插入元素
向单链表插入数据时,insert()方法有两个参数,element作为新的节点的数据,item则是单链表中已经存在的节点值,要插入的新节点的位置位于item之后,此时要插入节点的位置分为两种情况:
- 要插入的位置处于单链表的中间位置,此时将新的节点的next指针指向item的下一个元素,再将item的next指针指向新的元素即可。
- 要插入的位置处于单链表的尾部,此时只要将新的节点插入在最后一个节点之后即可。
仔细思考后发现,第二种情况是包含在第一中情况之内的,这是因为当item是单链表中最后一个元素时,其next指针指向为空,将其赋值给newNode的next指针并没有什么问题,因为在新建newNode时,其next指针本身就是空的。因此代码可以写成:
insert(item, element) {
let itemNode = this.find(item);
if(!itemNode) { // 如果item元素不存在
return;
}
let newNode = new Node(element);
newNode.next = itemNode.next; // 若currNode为最后一个节点,则currNode.next为空
itemNode.next = newNode;
this.size++;
}稍微有些复杂的函数基本阐述完毕,下面是单链表数据结构的整体代码:
class Node {
constructor(data) {
this.data = data;
this.prev = null;
this.next = null;
}
}
// 单链表
class SingleList {
constructor() {
this.size = 0; // 单链表的长度
this.head = new Node('head'); // 表头节点
this.currNode = ''; // 当前节点的指向
}
// 判断单链表是否为空
isEmpty() {
return this.size === 0;
}
// 获取单链表的最后一个节点
findLast() {
let currNode = this.head;
while (currNode.next) {
currNode = currNode.next;
}
return currNode;
}
// 单链表的遍历显示
display() {
let result = '';
let currNode = this.head;
while (currNode) {
result += currNode.data;
currNode = currNode.next;
if(currNode) {
result += '->';
}
}
console.log(result);
}
// 从当前位置向前移动 n 个节点。
advance(n, currNode = this.head) {
this.currNode = currNode;
while ((n--) && this.currNode.next) {
this.currNode = this.currNode.next;
}
return this.currNode;
}
// 在单链表中寻找item元素
find(item) {
let currNode = this.head;
while (currNode && (currNode.data !== item)) {
currNode = currNode.next;
}
return currNode;
}
// 显示当前节点
show() {
console.log(this.currNode.data);
}
// 获取单链表的长度
getLength() {
return this.size;
}
// 向单链表中插入元素
insert(item, element) {
let itemNode = this.find(item);
if(!itemNode) { // 如果item元素不存在
return;
}
let newNode = new Node(element);
newNode.next = itemNode.next; // 若currNode为最后一个节点,则currNode.next为空
itemNode.next = newNode;
this.size++;
}
// 在单链表中删除一个节点
remove(item) {
if(!this.find(item)) { // item元素在单链表中不存在时
return;
}
// 企图删除头结点
if (item === 'head') {
if (!(this.isEmpty())) {
return;
} else {
this.head.next = null;
return;
}
}
let currNode = this.head;
while (currNode.next.data !== item) {
// 企图删除不存在的节点
if (!currNode.next) {
return;
}
currNode = currNode.next;
}
currNode.next = currNode.next.next;
this.size--;
}
// 在单链表的尾部添加元素
append(element) {
let currNode = this.findLast();
let newNode = new Node(element);
currNode.next = newNode;
this.size++;
}
// 清空单链表
clear() {
this.head.next = null;
this.size = 0;
}
}单链表的测试案例:
let myList = new SingleList();
let arr = [3, 4, 5, 6, 7, 8, 9];
for(let i=0; i<arr.length; i++){
myList.append(arr[i]);
}
myList.display(); // head->3->4->5->6->7->8->9
console.log(myList.find(4)); // Node {data: 4, prev: null, next: Node}
myList.insert(9, 9.1);
myList.insert(3, 3.1);
myList.display(); // head->3->3.1->4->5->6->7->8->9->9.1
myList.remove(9.1);
myList.remove(3);
myList.display(); // head->3.1->4->5->6->7->8->9
console.log(myList.findLast()); // Node {data: 9, prev: null, next: null}
console.log(myList.advance(4)); // Node {data: 6, prev: null, next: Node}
console.log(myList.getLength()); // 7
myList.clear();
myList.display(); // head(4)、链表的应用
- 排序链表
暴力解法——借助数组排序
function sortInList(head) {
// 声明一个数组接收遍历的数据
let arr = []
while (head !== null) {
arr.push(head.val)
head = head.next
}
// 对数据进行排序
arr.sort(function(a, b) {
return a - b
})
// 声明一个新的链表接收数组中的元素
let node = new ListNode()
let cur = node
for(let i = 0; i <= arr.length - 1; i++){
cur.next = new ListNode(arr[i])
cur = cur.next
}
return node.next
}归并排序
function sortInList(head) {
// 当链表为空或只有一个元素时直接返回
if (head === null || head.next === null) {
return head
}
// 声明两个指针
let low = head
let fast = head.next
while (fast !== null && fast.next !== null) {
// 快指针会到达中点位置
low = low.next
fast = fast.next.next
}
let newList = low.next
low.next = null
//递归
let left = sortInList(head)
let right = sortInList(newList)
let result = new ListNode()
let cur = result
//使用 cur 存储 result,因为下面 result 会变动
while (left !== null && right !== null) {
if (left.val < right.val) {
result.next = left
left = left.next
} else {
result.next = right
right = right.next
}
result = result.next
}
result.next = left != null ? left : right;
return cur.next
}- 合并两个有序链表
归并排序
/**
* 单链表的定义
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
var mergeTwoLists = function(l1, l2) {
if (l1 === null) { return l2 }
if (l2 === null) { return l1 }
if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2)
return l1
} else {
l2.next = mergeTwoLists(l1, l2.next)
return l2
}
}- 环形链表
写个函数来判断链表是否有环,使用了快慢指针,如果快指针走到最后为null,说明链表没有环,如果两个指针在某个时刻相等了,则说明链表有环。
function isLoop (list) {
// 使用快慢指针
var p = list.head
var q = list.head
while (q) {
p = p.next
if (p.next) {
q = q.next.next
}
if (p === q) {
console.log('该链表有环')
return
}
}
console.log('该链表无环')
}
var myList = new SingleList()
var arr = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
arr.forEach(item => myList.append(item))
var C = myList.find('C')
var G = myList.findLast()
G.next = C
isLoop(myList)
// 输出:该链表有环5、矩阵
- 螺旋矩阵
- 旋转图像
6、树
(1)、认识树
树是一种非线性数据结构。
一棵树(tree)是由n(n>0)个元素组成的有限集合,其中:
- 每个元素称为结点(node);
- 有一个特定的结点,称为根结点或根(root);
- 除根结点外,其余结点被分成m(m>=0)个互不相交的有限集合,而每个子集又都是一棵树(称为原树的子树)。
树的概念:
- 度——也即是宽度,简单地说,就是结点的分支数。以组成该树各结点中最大的度作为该树的度,树中度为零的结点称为叶结点或终端结点。树中度不为零的结点称为分枝结点或非终端结点。除根结点外的分枝结点统称为内部结点。
- 深度——组成该树各结点的最大层次。
- 层次——根结点的层次为1,其他结点的层次等于它的父结点的层次数加1。
- 路径——对于一棵子树中的任意两个不同的结点,如果从一个结点出发,按层次自上而下沿着一个个树枝能到达另一结点,称它们之间存在着一条路径。可用路径所经过的结点序列表示路径,路径的长度等于路径上的结点个数减1。
- 森林——指若干棵互不相交的树的集合。
树的表示:
最长见的树的表示方式是 “广义表”,例如:
(A , ( B ( E ( K , L ) , F ) , C ( G ) , D ( H ( M ) , I , J ) ) )也可以使用 vn 图、柱状图 等表示法。
- 二叉树
- 完全二叉树
- 完整二叉树
- 二叉查找树
- AVL树
- 红黑树
- B树 和 B+树
- Trie树(前缀树或字典树)
- 对称二叉树
- 验证二叉树
二、数据结构与算法的特点
三、数据结构的应用场景
【参考文章】