问题描述
假设一个虚构的国家Combinatoria的硬币的面值为d1 ,d2,…,dk,其中d1 =1,而且其他di是大于1的不同整数。给定一个整数n >0,找零钱( making change)问题是求最少个数的硬币,其面值总和等于n。
(1)给出该问题的一个实例,说明使用标准的贪心算法只能得到次优解,也就是说,反复选择一个面值不超过n的最大面值硬币,直到选择的硬币的总和等于n。
(2)试描述一种解决找零钱问题的有效算法。求该算法的运行时间?
问题(1)
贪心算法是在对问题求解时,使用对于当前问题来说能够最大程度解决问题的最好选择。当对原问题进行求解后,继续对算法完成后未达到的数目进行贪心算法,直到子问题完成。即贪心算法每做一次贪婪选择就将所求问题简化为一个规模更小的子问题。
虽然贪心算法每一步都是局部最优解,但是由此产生的全局解有时不一定是最优的。例如该题给定面值为(1,4,5)三个面值的硬币,要求找零钱数为8.使用贪心算法可知8=5+1+1+1,共需四枚硬币,对于全局最优则为8=4+4共两枚。由此可知贪心算法并不一定会产生最优解。
对于贪心算法失败的问题,我们通常采用动态规划作为更好的算法选择。
问题(2)
①思路描述
对于该问题我们选取动态规划。动态规划就是将目标问题拆解为一个个子问题并直到子问题能够通过简单方法直接解决。对于解决完的子问题能够将其保存起来,以此来减少算法的重复计算,同时对子问题求解结果进行反推,最终推导至原问题的过程。
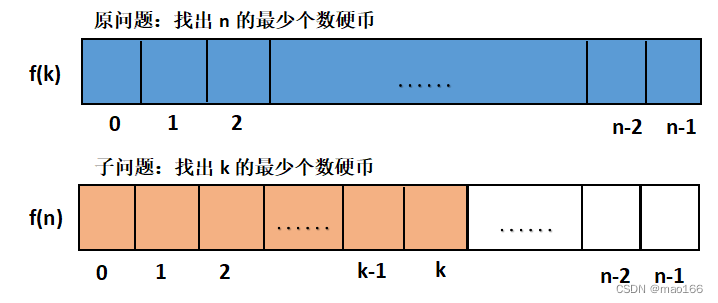
本问题中,我们将对于面值金额数为n,我们尝试不同硬币对面值数的影响,如果使用d1金额的硬币,该问题将变为凑出金额数n-d1的最小硬币数,如此同样可以继续划分为许多小问题。当金额数为k时,我们要求出n-di的最小硬币数。由此我们可以定义子问题为凑出金额n的最小硬币数,用f(n)表示。
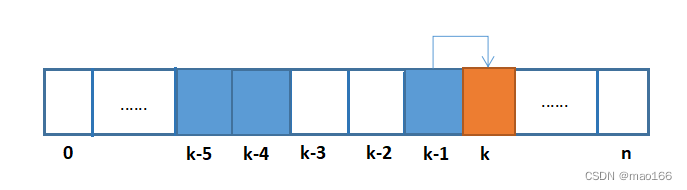
对于问题的递推关系,f(n)对于所需的最少个数硬币,我们以D={1,4,5}为例,则f(n)依赖于f(n-1)、f(n-4)、f(n-5),所有与f(n)有关联的值都在f(n)的左边,也就是说,子问题数组(DP数组)中的每个元素只依赖于其左边的元素。
由图可知,f(k)只与f(k-1)、f(k-4)、f(k-5)有关联,也就是说该DP数组中任意数只与之前的三个相关联。我们可以判断f(k-1)、f(k-4)、f(k-5)三个值中的最小值,f(n)即得该最小值加1。
②步骤描述
public int minCoinChange(int[] d, int n) {
// 子问题:
// f(k) = 凑出金额 k 的最小硬币数
// f(k) = min{ 1 + f(k - c) }
// f(0) = 0
int[] dp = new int[n+1];
Arrays.fill(dp, n + 1); // DP 数组初始化为正无穷大
dp[0] = 0;
for (int k = 1; k <= n; k++) {
for (int i : d) {
if (k >= i) {
dp[k] = Math.min(dp[k], 1 + dp[k-i]);
}
}
}
// 如果 dp[n] > n,认为是无效元素。
if (dp[n] > n) {
return -1;
} else {
return dp[n];
}
}
③时间复杂度
由算法可知,第k个子问题只和题目所求硬币数相关,算法计算次数每个状态只需要枚举i个面额,对于每个状态f(k)算法只计算一次,所以一共需要O(n*i)的时间复杂度。