一、键盘输入语句
使用键盘输入语句获取用户输入的数据:导入fmt包并调用 fmt.Scanln() 或 fmt.Scanf()。
1. 调用fmt.Scanln()

package main
import (
"fmt"
)
func main() {
// 接收 姓名,年龄,薪水,是否通过考试
var name string
var age int
var salary float64
var exam bool
fmt.Println("请输入姓名: ")
fmt.Scanln(&name)
fmt.Println("请输入年龄: ")
fmt.Scanln(&age)
fmt.Println("请输入薪水: ")
fmt.Scanln(&salary)
fmt.Println("是否通过考试(true/false): ")
fmt.Scanln(&exam)
fmt.Printf("姓名: %s, 年龄: %d, 薪水: %f, 是否通过考试: %t\n", name, age, salary, exam)
}
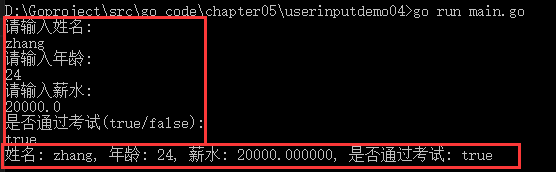
输出结果为:
2. 调用 fmt.Scanf()
fmt.Scanf():可以按指定的格式输入。
package main
import (
"fmt"
)
func main() {
// 接收 姓名,年龄,薪水,是否通过考试
var name string
var age int
var salary float64
var exam bool
fmt.Println("请输入姓名, 年龄, 薪水, 是否通过考试, 用空格隔开:")
fmt.Scanf("%s %d %f %t", &name, &age, &salary, &exam)
fmt.Printf("姓名: %s, 年龄: %d, 薪水: %f, 是否通过考试: %t\n", name, age, salary, exam)
}
输出结果为:
二、进制转换
对于整数,有四种表示方式:二进制、十进制、八进制 (以数字0开头表示) 和十六进制 (以0x或0X开头表示)。
1. 其他进制转十进制
1) 二进制转十进制
规则: 从最低位 (最右边) 开始,将每个位上的数提取出来,乘以2的(位数-1)次方,然后求和。
比如: ( 1011 ) 2 = 1 × 2 0 + 1 × 2 1 + 0 × 2 2 + 1 × 2 3 = ( 11 ) 10 (1011)_2=1 \times 2^0 + 1 \times 2^1 + 0 \times 2^2 +1 \times 2^3=(11)_{10} (1011)2=1×20+1×21+0×22+1×23=(11)10 或 ( 1011 ) 2 = 2 3 + 2 1 + 2 0 = ( 11 ) 10 (1011)_2=2^3+2^1+2^0=(11)_{10} (1011)2=23+21+20=(11)10。
2) 八进制转十进制
规则: 从最低位 (最右边) 开始,将每个位上的数提取出来,乘以8的(位数-1)次方,然后求和。
比如: ( 0123 ) 8 = 3 × 8 0 + 2 × 8 1 + 1 × 8 2 = ( 83 ) 10 (0123)_8=3 \times 8^0 + 2 \times 8^1 + 1 \times 8^2 =(83)_{10} (0123)8=3×80+2×81+1×82=(83)10。
3) 十六进制转十进制
规则: 从最低位 (最右边) 开始,将每个位上的数提取出来,乘以16的(位数-1)次方,然后求和。
比如: ( 0 x 34 A ) 16 = 10 × 1 6 0 + 4 × 1 6 1 + 3 × 1 6 2 = ( 842 ) 10 (0\text{x}34A)_{16}=10 \times 16^0 + 4 \times 16^1 + 3 \times 16^2 = (842)_{10} (0x34A)16=10×160+4×161+3×162=(842)10。
2. 十进制转其他进制
1) 十进制转二进制
规则: 将该数不断除以2,直到商为0为止,然后将每步得到的余数倒过来,得到对应的二进制。
比如: 56 ÷ 2 = 28...0 , 28 ÷ 2 = 14...0 , 14 ÷ 2 = 7...0 , 7 ÷ 2 = 3...1 , 3 ÷ 2 = 1...1 , 1 ÷ 2 = 0...1 56 \div 2 = 28...0, 28 \div 2 = 14...0, 14 \div 2 = 7...0, 7 \div 2 = 3...1, 3 \div 2 = 1...1, 1 \div 2 = 0...1 56÷2=28...0,28÷2=14...0,14÷2=7...0,7÷2=3...1,3÷2=1...1,1÷2=0...1,因此 ( 56 ) 10 = ( 111000 ) 8 (56)_{10} = (111000)_8 (56)10=(111000)8。
2) 十进制转八进制
规则: 将该数不断除以8,直到商为0为止,然后将每步得到的余数倒过来,得到对应的八进制。
比如: 156 ÷ 8 = 19...4 , 19 ÷ 8 = 2...3 , 2 ÷ 8 = 0...2 156 \div 8 = 19...4, 19 \div 8 = 2...3, 2 \div 8 = 0...2 156÷8=19...4,19÷8=2...3,2÷8=0...2,因此 ( 156 ) 10 = ( 0234 ) 8 (156)_{10} = (0234)_8 (156)10=(0234)8。
3) 十进制转十六进制
规则: 将该数不断除以16,直到商为0为止,然后将每步得到的余数倒过来,得到对应的十六进制。
比如: 356 ÷ 16 = 22...4 , 22 ÷ 16 = 1...6 , 1 ÷ 16 = 0...1 356 \div 16 = 22...4, 22 \div 16 = 1...6, 1 \div 16 = 0...1 356÷16=22...4,22÷16=1...6,1÷16=0...1,因此 ( 356 ) 10 = ( 0 x 164 ) 16 (356)_{10} = (0\text{x}164)_{16} (356)10=(0x164)16。
3. 二进制转八进制和十六进制
1) 二进制转八进制
规则:将二进制数从最低位开始,每三位一组转成对应的八进制。
比如: 11010101 = ( 011 ) ( 010 ) ( 101 ) = 0325 11010101=(011) (010) (101)=0325 11010101=(011)(010)(101)=0325。
2) 二进制转十六进制
规则:将二进制数从最低位开始,每四位一组转成对应的十六进制。
比如: 11010101 = ( 1101 ) ( 0101 ) = 0 xD 5 11010101=(1101)(0101)=0\text{x}\text{D}5 11010101=(1101)(0101)=0xD5。
4. 其他进制转二进制
1) 八进制转二进制
规则:将八进制的每一位数,转换成一个三位的二进制。
比如: 0325 = ( 011 ) ( 010 ) ( 101 ) = 11010101 0325=(011) (010) (101)=11010101 0325=(011)(010)(101)=11010101
2) 十六进制转二进制
规则:将十六进制的每一位数,转换成一个四位的二进制。
比如: 0 xD 5 = ( 1101 ) ( 0101 ) = 11010101 0\text{x}\text{D}5=(1101)(0101)=11010101 0xD5=(1101)(0101)=11010101