在神经网络模型优化的过程中,会遇到许多问题,比如如何设置学习率的问题,我们可通过指数衰减的方式让模型在训练初期快速接近较优解,在训练后期稳定进入最优解区域;针对过拟合问题,通过正则化的方法加以应对;滑动平均模型可以让最终得到的模型在未知数据上表现的更加健壮。
一、学习率的设置
学习率设置既不能过大,也不能过小。TensorFlow提供了一种更加灵活的学习率设置方法——指数衰减法。该方法实现了指数衰减学习率,先使用较大的学习率来快速得到一个比较优的解,然后随着迭代的继续逐步减小学习率,使得模型在训练后期更加稳定,缓慢平滑得达到最优值。
tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate,staircase=False, name=None)
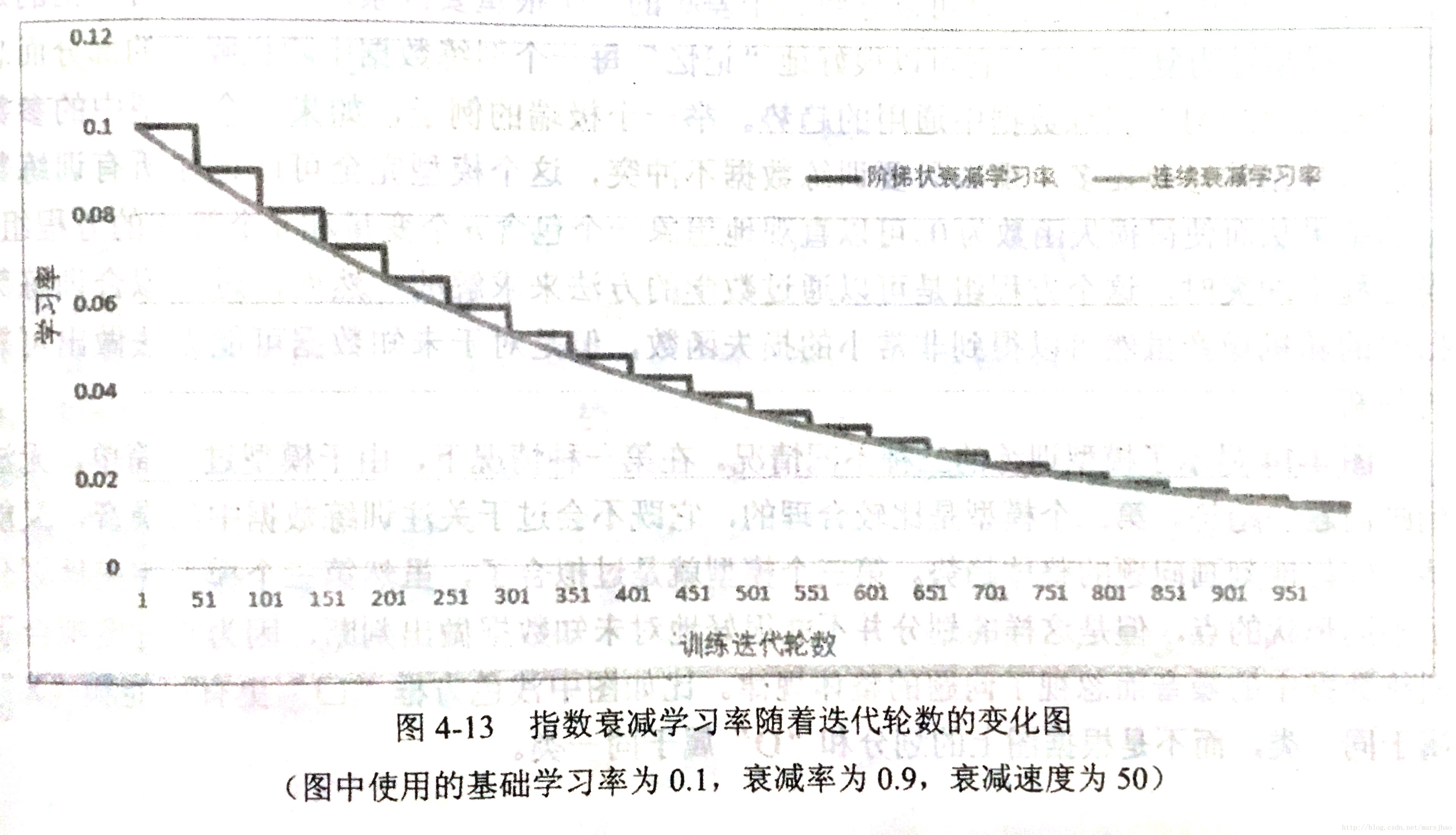
该函数会指数级减小学习率,实现每轮实际优化时的衰减后的学习率decayed_learning_rate = learning_rate * decay_rate ^ (global_step /decay_steps),learning_rate为设定的出事学习率,decay_rate为衰减系数,decay_steps为衰减速度。如下图,参数staircase=False时,学习率变化趋势为浅色部分;staircase=True时为深色部分,使得学习率变化为阶梯函数(staircase function),这种设置的常用应用场景是每完整地过完一遍训练数据,学习率就减小一次。
使用示例:learning_rate =tf.train.exponential_decay(starter_learning_rate, global_step, 100000, 0.96,staircase=True)。
二、过拟合问题
1. 过拟合问题及其解决方法
所谓过拟合问题,指的是当一个模型过于复杂后,它可以很好地记忆每一个训练数据中随机噪声的部分而忘记了要去学习训练数据中通用的趋势。
为了避免过拟合问题,常用的方法是正则化(Regularization),思想是在损失函数中加入刻画模型复杂程度的指标,将优化目标定义为J(θ)+λR(w),其中R(w)刻画的是模型的复杂程度,包括了权重项w不包括偏置项b