【leetcode 力扣刷题】反转链表+递归求解

反转链表+递归求解

206. 反转链表
92.反转链表Ⅱ
- 反转left到right间节点的next指向
234.回文链表

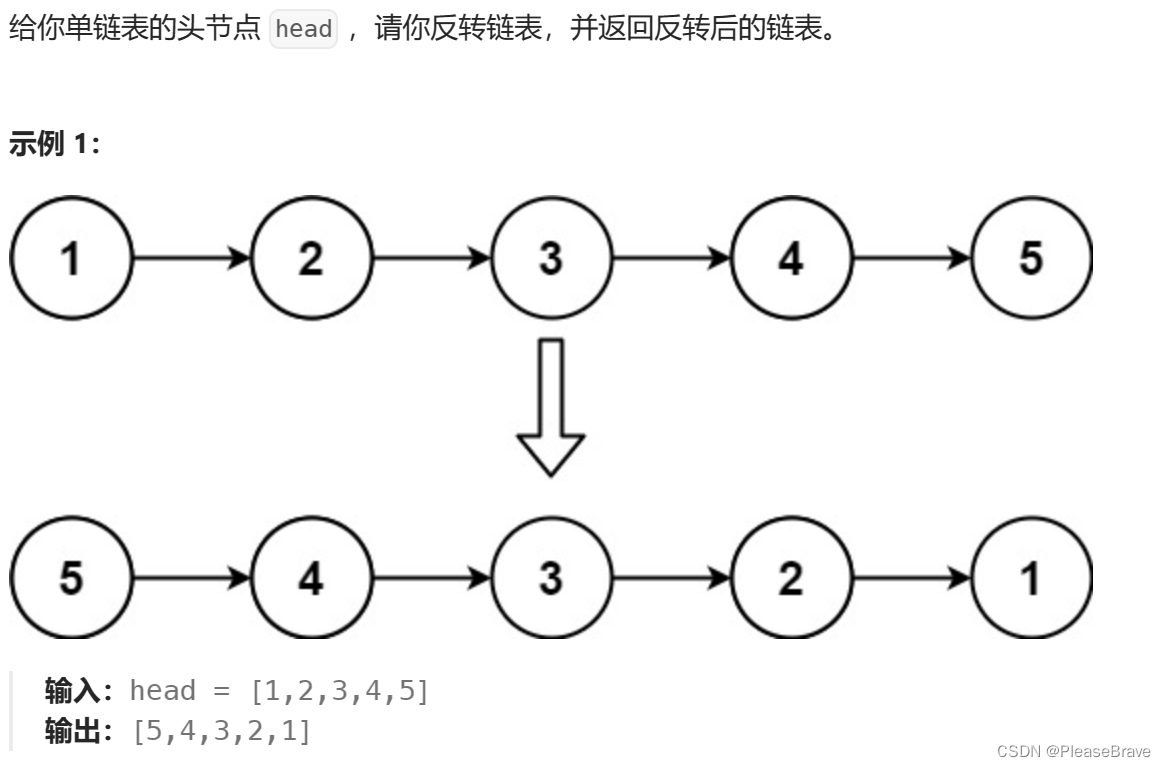
206. 反转链表

题目链接：206.反转链表
题目内容：
在这里插入图片描述
理解题意：没有特殊要求，就是把链表反转，相当于从之前的末尾指向开头。

解法①：取下一个节点在当前头节点前插入

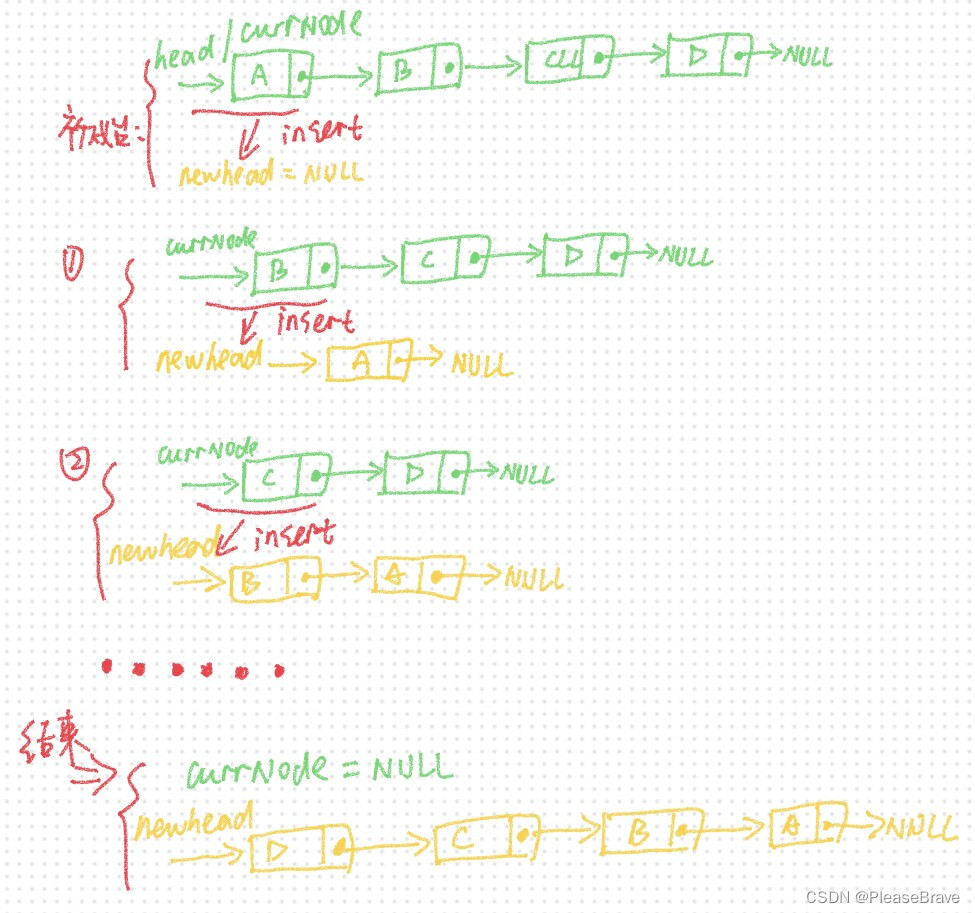
第一种方法最容易想到，从前往后遍历链表的同时，每次从原链表中取下当前节点，插入到新链表的开头。这里的新链表，实际就是该节点之前所有节点已经反转后构成的链表，过程如下：
5 在这里插入图片描述

代码如下（C++）：

//依次取出每个节点，并将其插入在新链表的头部
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        //如果链表为空直接返回空指针
        if(!head)
            return nullptr;
        ListNode *currNode = head;
        //初始化新链表，为空
        ListNode *newhead = nullptr;
        while(currNode != nullptr){   
            ListNode *tmp = currNode->next;
            // currNode插入在新链表的头部
            currNode->next = newhead; 
            newhead = currNode;
            //currNode移到下一个节点
            currNode = tmp;         
        }
        //返回新链表
        return newhead;
    }
};

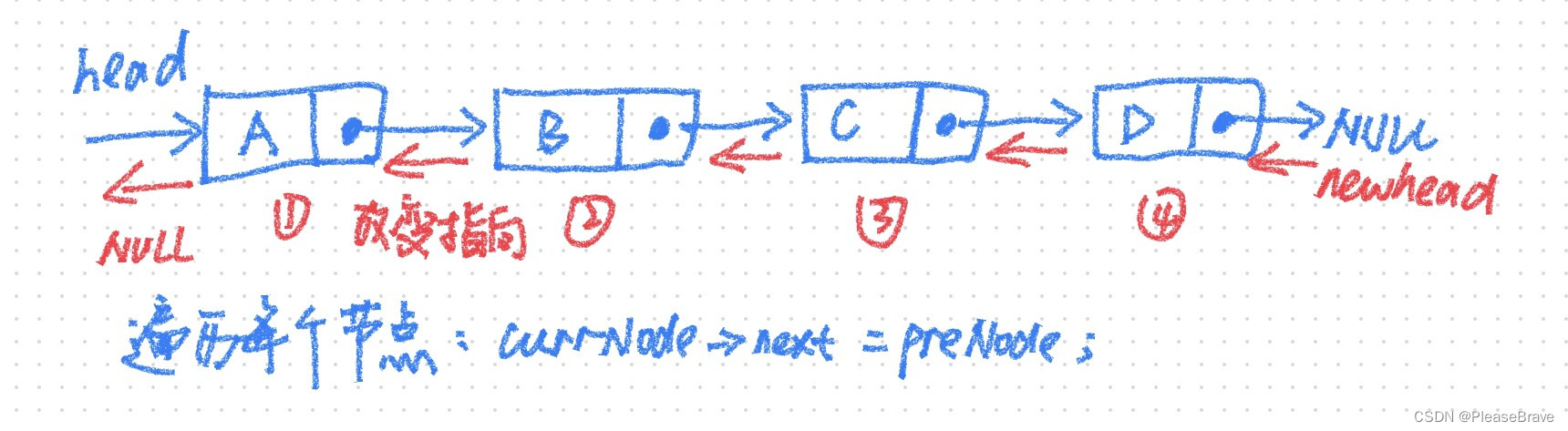
解法②：反转每个节点next的指向

假设原链表中一前一后两个节点：preNode和currNode，指向是preNode->next = currNode；反转后链表中这俩节点的指向是currNode->next = preNode。既然如此，那么可以在遍历链表中节点的时候【当前节点就用currNode】，直接改变其指针域：
在这里插入图片描述
代码如下（C++）：

//遍历链表每个节点，将next改变成指向前面；
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* prev = NULL;  //prev前驱节点初始化为null
        ListNode* currNode = head;  //当前节点初始化为头节点
        while(currNode){
            ListNode* tmp = currNode->next;
            //改变当前节点指针，指向其前驱节点
            currNode->next = prev;
            //prev和currNode都向后移动，遍历链表节点
            prev = currNode;
            currNode = tmp;
        }
        return prev; //最后prev就是新的head，currNode已经为null了
    }
};

本质上解法①和解法②是一样的，只是从两个角度去理解“反转”。

解法③：递归

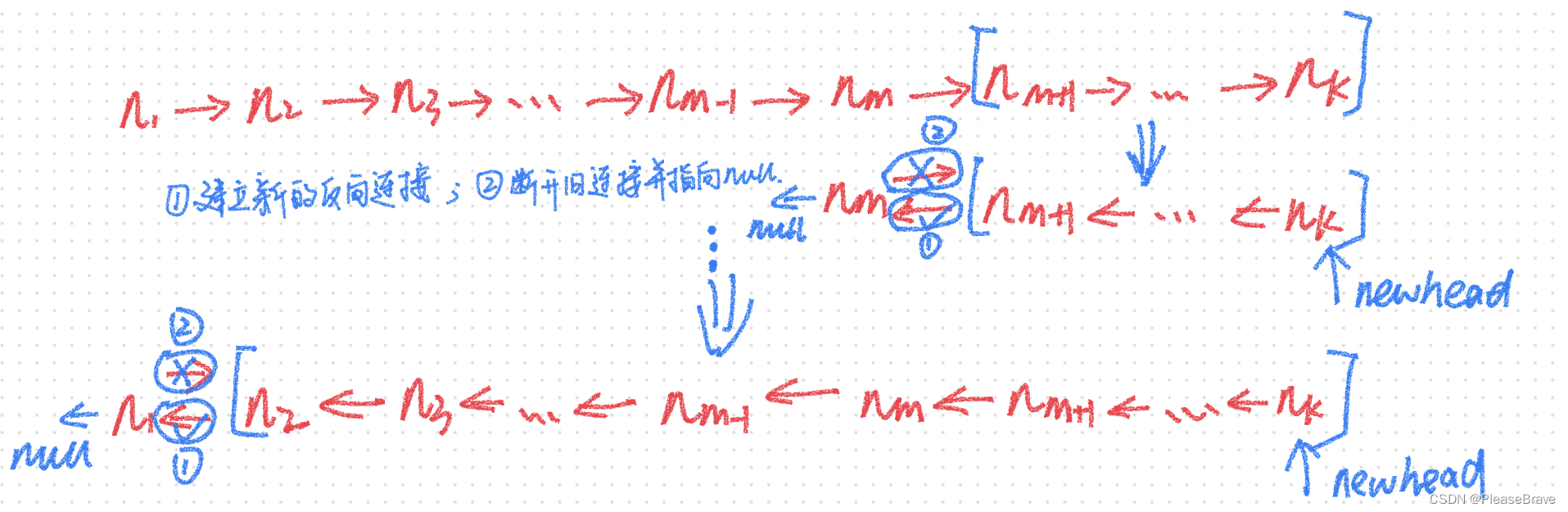
从前往后遍历链表节点，并使用递归方法的时候，要到最后一个节点才开始往前返回，那么就是先反转后半截链表，再向前返回到当前的节点，再对当前节点处理。假设链表有k个节点：

递归到第k个节点的时候，递归终止，并且这最后一个节点就是整个链表反转后的头节点，直接返回该节点地址；
m+1个节点作为后半截已经反转后的链表的尾节点，其next指向null；现在将m+1和m个节点连接起来，m+1的next指向m；m+1个节点是后半截反转后的尾节点，怎么找到m+1个节点呢？【对于当前第m个节点，其next依然指向m+1个节点，因此直接currNode->next->next = currNode，使m+1个节点的next指向当前第m个节点】；
m现在作为m-1之后剩余链表反转后的尾节点，其next应该指向null；
到第m个节点的时候，m+1~k个节点已经反转了，并返回了新的头节点；即便是加上第m个节点并反转，第m个节点也是加在反转后链表的尾部，因此上一步返回的新头节点是整个链表反转后头节点，因此要一直向前返回这个地址；

整个过程如图所示：在这里插入图片描述

代码如下（C++）：

class Solution{
public:
    ListNode* reverseList(ListNode* head) {
    	//如果链表为空，直接返回
    	//如果已经遍历到最后一个节点，最后一个节点就是反转后的头节点，直接返回
        if(head == nullptr || head->next == nullptr)
            return head;
        //当前head之后的链表已经反转了，并返回反转后的新头节点指针     
        ListNode *newhead = reverseList(head->next);
        //将head->next的next指针指向当前head，反转
        head->next->next = head;
        //断开当前head和head->next之间原本的连接
        head->next = nullptr;
        //返回的新头节点是整个链表反转后的头节点，因此一直返回newhead
        return newhead;
    }    
};

92.反转链表Ⅱ

题目链接：92.反转链表Ⅱ
题目内容：
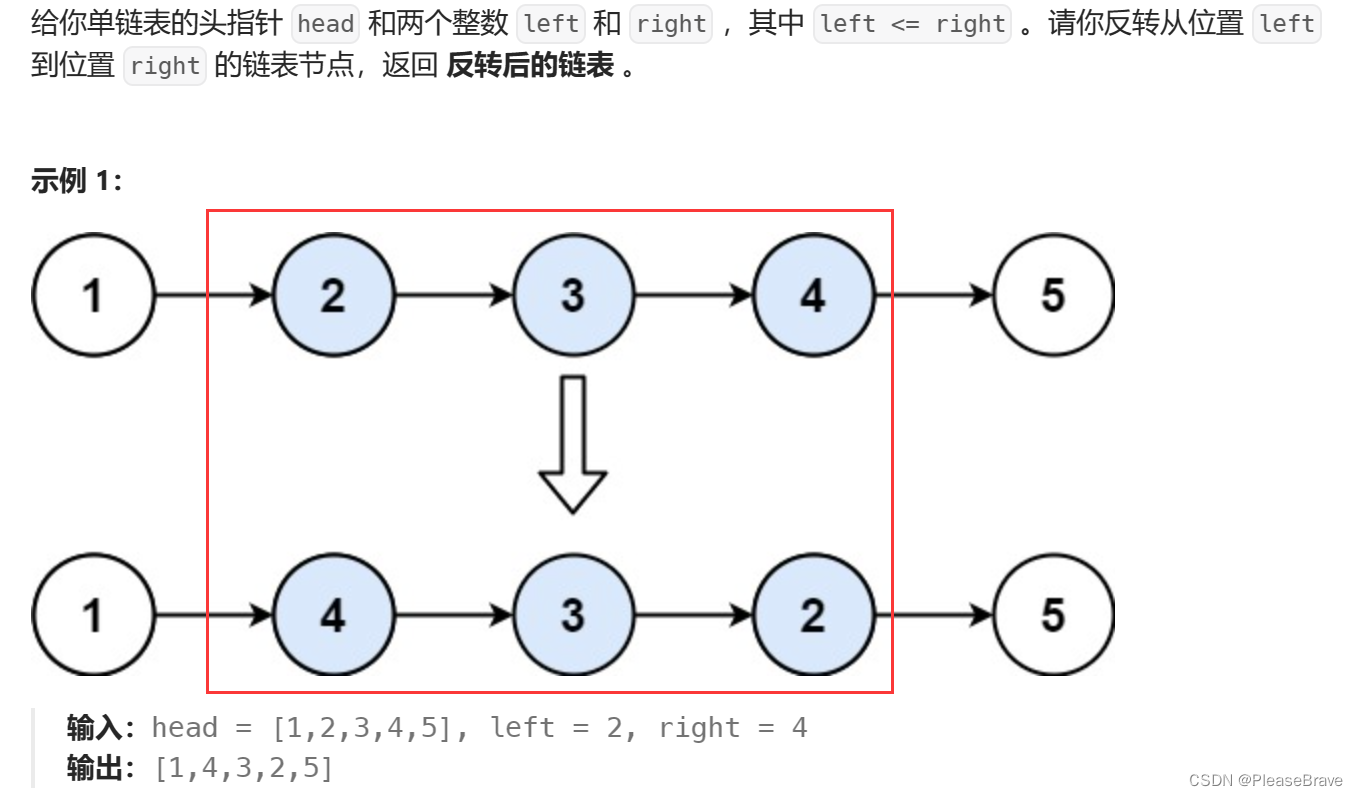
在这里插入图片描述
理解题意：在对整个链表反转的基础上，增加了限制条件——只反转给定的left~right位置间的节点。完成left~right的反转后，还需要让left之前的节点left_pre->next指向right；还需要让left->next指向right->next。
以下解法为一遍访问链表完成left~right之间的节点的反转：

反转left到right间节点的next指向

整个过程分为以下几步：

需要记录的节点有left、right、left前面一个节点left_pre和right后面一个节点right->next；
先遍历链表找到left_pre和left；
从left开始到right，用反转链表题目的解法，反转这一段链表；用到pre和currNode两个变量保存当前要改变指向的节点、以及之前的一个节点；
上一步循环结束时，pre就是right，currNode就是right->next；此时建立新连接：left_pre->next = right【即pre】，left->next = right->next【即currNode】；得到完整链表；

上述过程为一次遍历链表，在遍历的过程中改变left~right间的指向。全部代码如下（C++）：

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
    	//如果left和right相等，没有节点要反向
        if(left == right) 
        	return head;
        //存left和left前面一个节点的地址
        ListNode *leftNode = head, *left_prev = NULL;
        //定位到leftNode，并保存left_pre
        for(int i=1; i<left && leftNode; i++ ){
            left_prev = leftNode;
            leftNode = leftNode->next;
        } 
        //left~right间反向时用到的变量  
        ListNode *prev, *currNode;   //当前节点和当前节点的前一个节点    
        prev = leftNode;
        currNode = prev->next;
        while(currNode && left < right){
            ListNode* tmp = currNode->next;
            //反转next指向
            currNode->next = prev;
            //pre和currNode都向前移动，遍历left~right间节点
            prev = currNode;
            currNode = tmp;
            left++;
        }  //循环结束后pre是right节点，currNode是right->next节点
        //左边节点leftNode指向right->next
        leftNode->next = currNode;
        //判断leftnode是不是头节点
        if(left_prev  != NULL) //如果不是，left前面一个节点指向right节点
            left_prev->next = prev;
        else //如果是，新的头节点就是right节点
            head =  prev;        
        return head;
    }
};

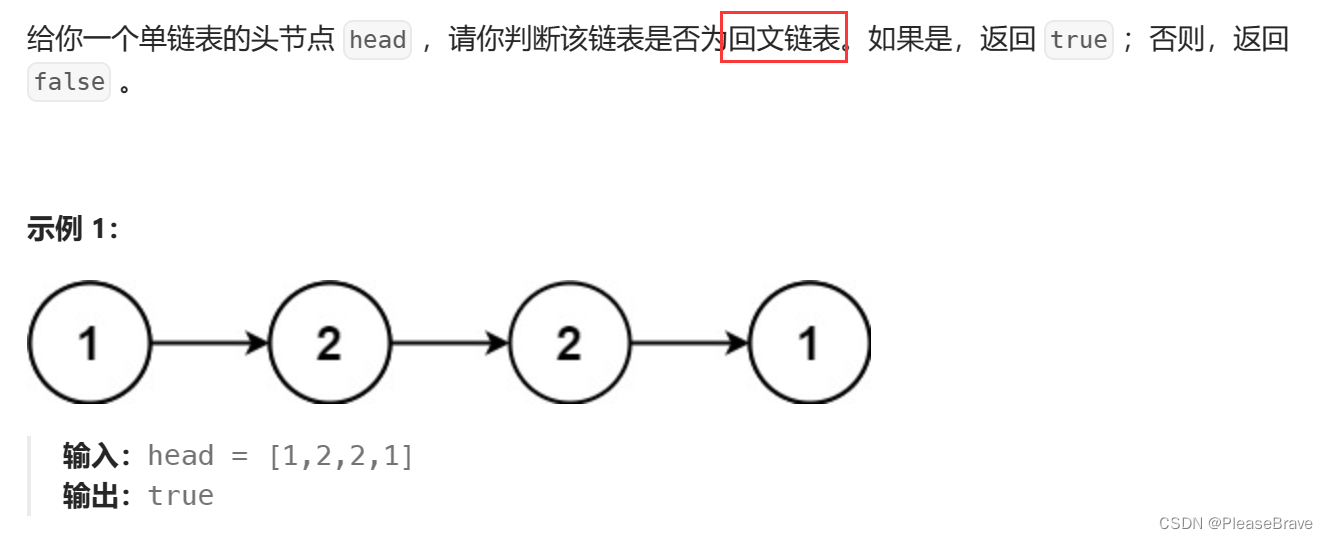
234.回文链表

题目链接：203.回文链表
题目内容：
在这里插入图片描述
理解题意：实际就是判断是不是回文【回文数：从前往后、从后往前是一样的，比如0123210；判断：两个指针一个开头，一个结尾，逐个对比，全相等就是回文】，只是换成了在链表上判断。但是由于链表只能向next一个方向遍历，不像数组、string等可以用下标index去定位。因此有两种解法：

遍历链表，并且把链表各个节点的val按照顺序存在vector里面，然后在vector上比较；
直接在链表上比较；

直接在链表上进行比较又有两种方法：

遍历链表的同时，用上面的反转链表方法，把前半部分链表反转；反转后的前半部分链表和后半部分链表的节点逐个对比，val值都一样即为回文；
递归求解：因为递归到最后一个节点才递归终止，能够知道当前的节点的val；一开始的head还在开头，就能实现首尾比较；一旦不相等，其他节点就不用比较了，直接向前返回false；如果相等，后面的节点向前返回到前面一个节点进行操作，前面节点需要向后移动；

解法①：将链表元素存在数组中，在数组上判断回文

这个方法最好理解，也没有什么难度，先遍历链表取出各个节点的val，按原顺序存在vector中，在vector上实现回文判断，需要额外的空间……
代码如下（C++）：

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> val;  //数组用于存储链表节点的val
        ListNode *currNode = head;
        //遍历链表节点，并保存各个节点的val
        while(currNode){
            val.emplace_back(currNode->val);
            currNode = currNode->next;
        }
        //双指针，判断数组是否是回文的
        for(int i = 0, j = val.size() - 1; i < j ; i++,j--){
      		//一旦有节点不相等，就不是回文
            if(val[i] != val[j])
                return false;
        }
        return true;
    }
 };

解法②：在链表上反转前半部分链表，和后半部分对比

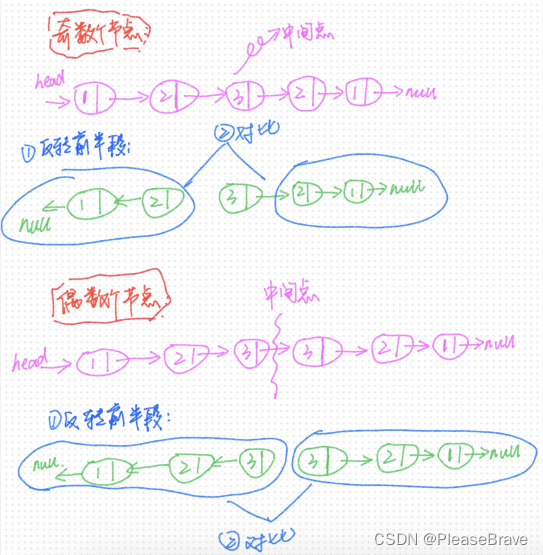
这个方法是一次遍历链表，遍历的过程中，同时反转链表，这个反转结束的地方是链表的中间点；从这个中间点开始，用一个指针逐个向前访问前面一段链表的节点，再用一个指针逐个向后访问后面一段链表的节点；并比较节点的val，判断是否是回文，过程如下所示：
在这里插入图片描述
这里有个问题，就是如何找到链表的中间节点：用一个slow指针，一个fast指针，初始slow和fast都为head【没有附加头结点时】，每次slow向后移动一个slow = slow->next，但是fast向后移动两个fast = fast->next->next。当fast->next =null的时候【有偶数个节点】或fast->next->next = null的时候【有奇数个节点】终止，此时的slow就定位在中间节点。
代码实现（C++）：

class Solution {
public:
    bool isPalindrome(ListNode* head) {
    	//如果只有一个节点直接返回true
        if(head->next== nullptr)
            return true;
        //用slow、fast来寻找链表的中间点，prev是slow前面一个节点，辅助完成反转操作       
        ListNode *slow = head,*fast = head, *prev = NULL;
        //找到中间节点，并同时反转前半段链表
        while(fast->next && fast->next->next){  
            fast = fast->next->next;       
            ListNode* tmp = slow->next;
            slow->next = prev;
            prev = slow;
            slow = tmp;                       
        } 
        //上述循环结束时，slow是(n+1)/2节点
        //比如5个节点，slow在第3个节点；6个节点，slow在第3个节点
        //且此时slow指向是原始的指向
        ListNode *right_head, *left_head; //左右两段一段向前，一段向后链表的头节点
        right_head = slow->next;  //右边头节点就是slow->next
        //偶数个节点，slow需要反转连接
        if(fast->next){            
            slow->next = prev;
            left_head = slow;
        }
        //奇数个节点，slow不需要反转连接
        else{ 
            left_head = prev;  
        }
        //两段链表节点逐个对比val
        while(left_head!=nullptr && right_head!=nullptr){
            if(left_head->val != right_head->val)
                return false;
            left_head = left_head->next;
            right_head = right_head->next;
        }
        return true;
    }
};

其中奇数个节点、偶数个节点需要分开讨论，写代码的时候要区分开。

解法③：递归

这里的递归求解参考的力扣官方题解。因为递归到最后一个节点才递归终止，能够知道当前的节点的val；一开始的frontNode还在开头，就能实现首尾比较；一旦不相等，其他节点就不用比较了，直接向前返回false；如果相等，后面的节点向前返回到前面一个节点进行操作，前面节点需要向后移动；
递归的时候需要一个指针，递归到最后向前返回；那么还需要一个外部指针，递归返回后，它向后移动。
代码实现（C++）：

class Solution {
public:
    ListNode* frontNode; //需要定义一个全局的变量
    bool recursivelyCheck(ListNode *currNode){
        if(currNode){
            //后面已经有节点和前面的不相等，中间一截不用比较了直接向上返回false
            if(!recursivelyCheck(currNode->next))
                return false;
            //对比当前元素与前面对应元素是否一样
            if(currNode->val != frontNode->val)
                return false;
            //将前面元素向后面移动一个
            frontNode = frontNode->next;
        }
        return true;
    }
    bool isPalindrome(ListNode* head) {
        frontNode = head; 
        return recursivelyCheck(head);
    }
};