Bootstrap

AVL树（C语言实现）

AVL树（C语言实现）

​ 插入、删除和查找是树的几种基本操作。对于插入或删除这个动作而言，其所花时间为常数时间，整个操作的大部分时间在于找到要插入或删除的节点所花的时间。树的高度越大，查找所花的时间也就越大，为减小对树进行操作所花的时间，我们总希望树越矮越好。对于同样的一组集合，左边的树更像一个链表，其平均查找次数大于右边的树。

组合1.png

相关概念

  • 树的高度：关于树的高度，众说纷纭。此处定义为根节点到叶节点所经过的路径数的最大值。对某个节点而言，为该节点到叶节点所经过的路径数的最大值。若节点为叶节点，则该节点高度为0，否则等于其左右子树的高度的最大值加一。
  • 平衡因子：定义为节点左子树的高度与节点右子树高度之差。若平衡因子的绝对值大于1，说明该节点为失衡节点。

失衡情况

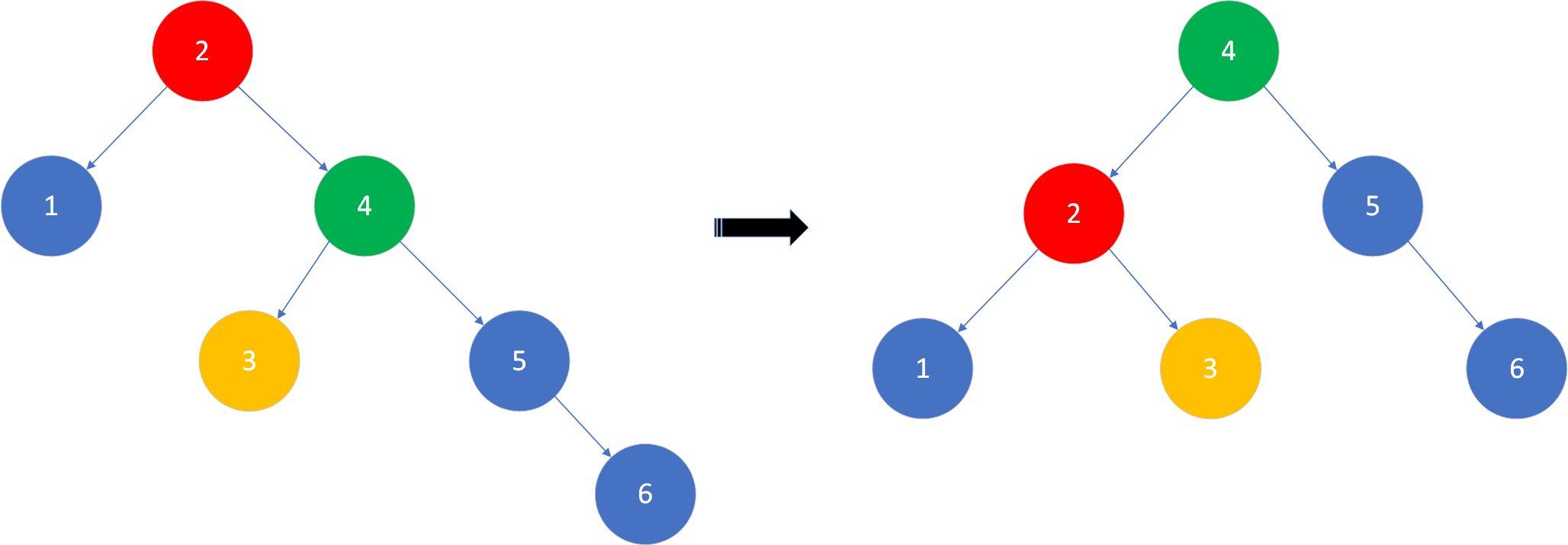
  • L-L型失衡：失衡节点的平衡因子大于1，失衡发生在失衡节点的左孩子的左子树上。表现为：左孩子的高度大于右孩子的高度，左孩子的左子树的高度大于其右子树的高度。为使树平衡，应对失衡节点进行右旋操作（顺时针旋转），失衡节点的左孩子更新为失衡节点左孩子的右子树，失衡节点的原左子树的右孩子更新为失衡节点，新的根节点为失衡节点的原左孩子。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CaGUDU1q-1644339259920)(https://s2.loli.net/2022/01/21/TAVasdO1UmGbpkE.png)]

  • R-R型失衡：失衡节点的平衡因子小于-1，失衡发生在失衡节点的右孩子的的右子树上。表现为：右孩子的高度大于左孩子的高度，右孩子的右子树的高度大于其左子树的高度。为使树平衡，对失衡节点进行左旋操作（顺时针旋转），操作与L-L型的调整操作类似。RRRotation.png

  • L-R型失衡：失衡节点的平衡因子大于1， 失衡发生在失衡节点的左孩子的右子树上，注意和失衡节点的左孩子的右子树的左右子树无关，下边的R-L型失衡同理。表现为：左孩子的高度大于右孩子的高度，且左孩子的右子树的高度大于左孩子左子树的高度。首先对失衡节点的左孩子进行左旋操作（逆时针旋转），再对失衡节点进行右旋操作（顺时针旋转）。可以发现，L-R失衡的调整操作是R-R型调整和L-L型失衡调整的组合，R-L型失衡的调整也是同一个道理。LRRotation.png

  • R-L型失衡：失衡节点的平衡因子小于-1，失衡发生在失衡节点的右孩子的左子树上。表现为：失衡节点的右孩子的高度大于左孩子的高度，且右孩子的左子树高度大于右子树的高度。首先对失衡节点的右孩子进行右旋操作（顺时针旋转），再对失衡节点进行左旋操作（逆时针旋转）。RLRotation.png

建树思路

​ 从空树开始，直接插入一个节点；对于非空的树，找到插入位置（若插入的元素已存在则不用操作），插入节点，检查树中是否有失衡节点，若有，则进行调整。建树思路清晰简单，但实现起来需要考虑许多细节。情况是否考虑周全，语言的特性都在考虑的范围内。

C代码实现

  • 节点的定义

    struct TreeNode{
    struct TreeNode *left;
    struct TreeNode *right;
    struct TreeNode *parent;
    ElementType element;
};
typedef struct TreeNode Node;

  • 节点的高度

    int GetHeight(Node *node)
{
    if ( node == NULL )
        return -1;

    int leftchildheight = GetHeight(node->left);
    int rightchildheight = GetHeight(node->right);
    return ( leftchildheight > rightchildheight ? leftchildheight: rightchildheight) + 1;
}

  • 找到插入的位置（节点）

    Node *FindNodeToBeInserted(ElementType element, Node *root)
{
    Node *tmp = root;
    Node *parent = NULL;

    while ( tmp != NULL )
    {
        if ( element < tmp->element )
        {
            parent = tmp;
            tmp = tmp->left;
        }
        else if ( element > tmp->element )
        {
            parent = tmp;
            tmp = tmp->right;
        }
        else
        {
            parent = tmp;
            tmp = NULL;
        }
    }

    return parent;
}

  • 插入

    ​ 节点的内容包括此节点的父亲，因此插入后，插入节点的父亲应该指向被插入的节点，方便后续操作。

    void Insert(ElementType element, Node *insert_ndoe)
{
    if ( element < insert_ndoe->element )
    {
        Node *node;
        node = (Node*)malloc(sizeof(Node));
        node->element = element;
        node->left = NULL;
        node->right = NULL;
        node->parent = insert_ndoe;
        insert_ndoe->left = node;
    }

    else if ( element > insert_ndoe->element )
    {
        Node *node;
        node = (Node*)malloc(sizeof(Node));
        node->element = element;
        node->left = NULL;
        node->right = NULL;
        node->parent = insert_ndoe;
        insert_ndoe->right = node;
    }
}

  • 查找失衡节点

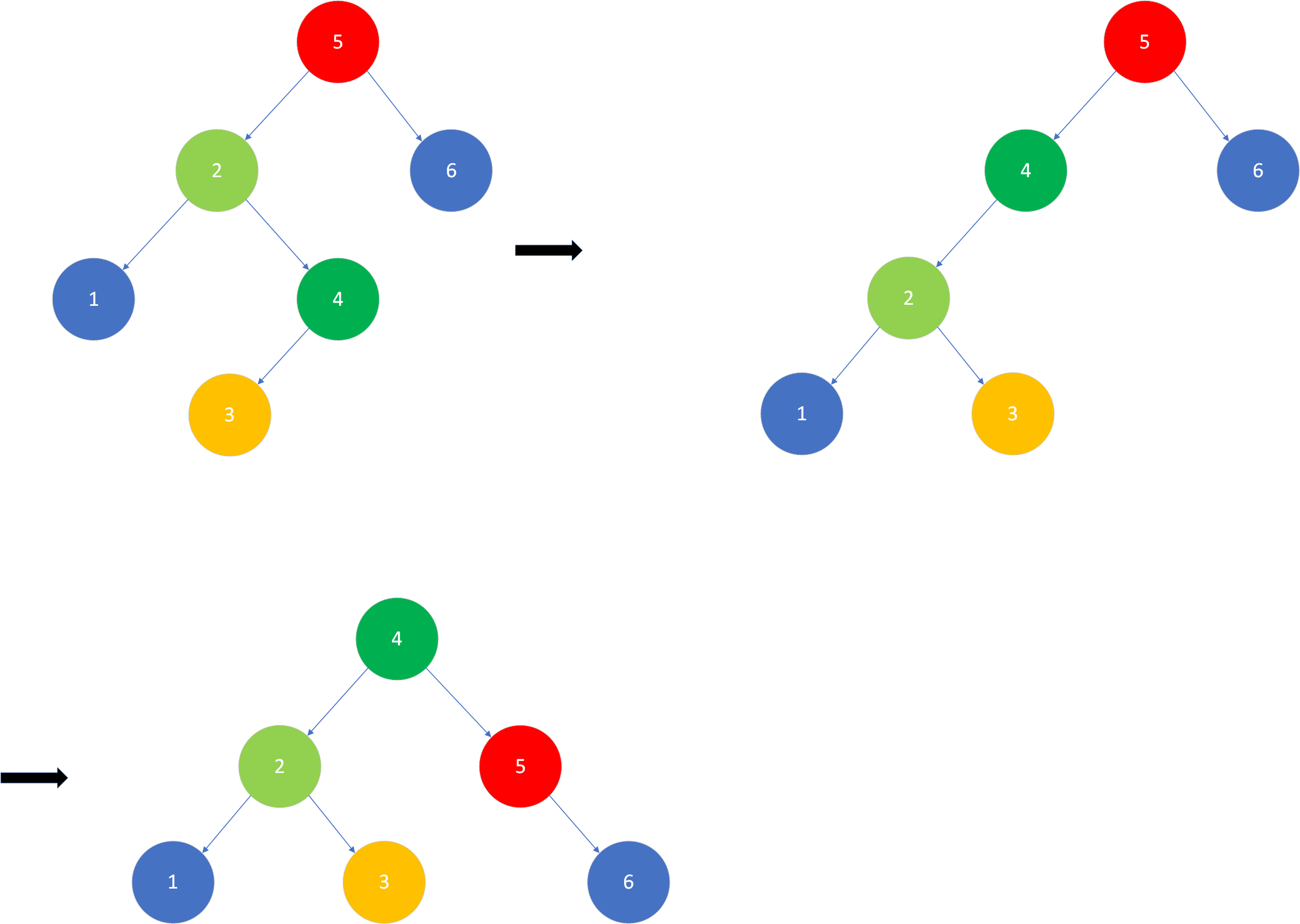
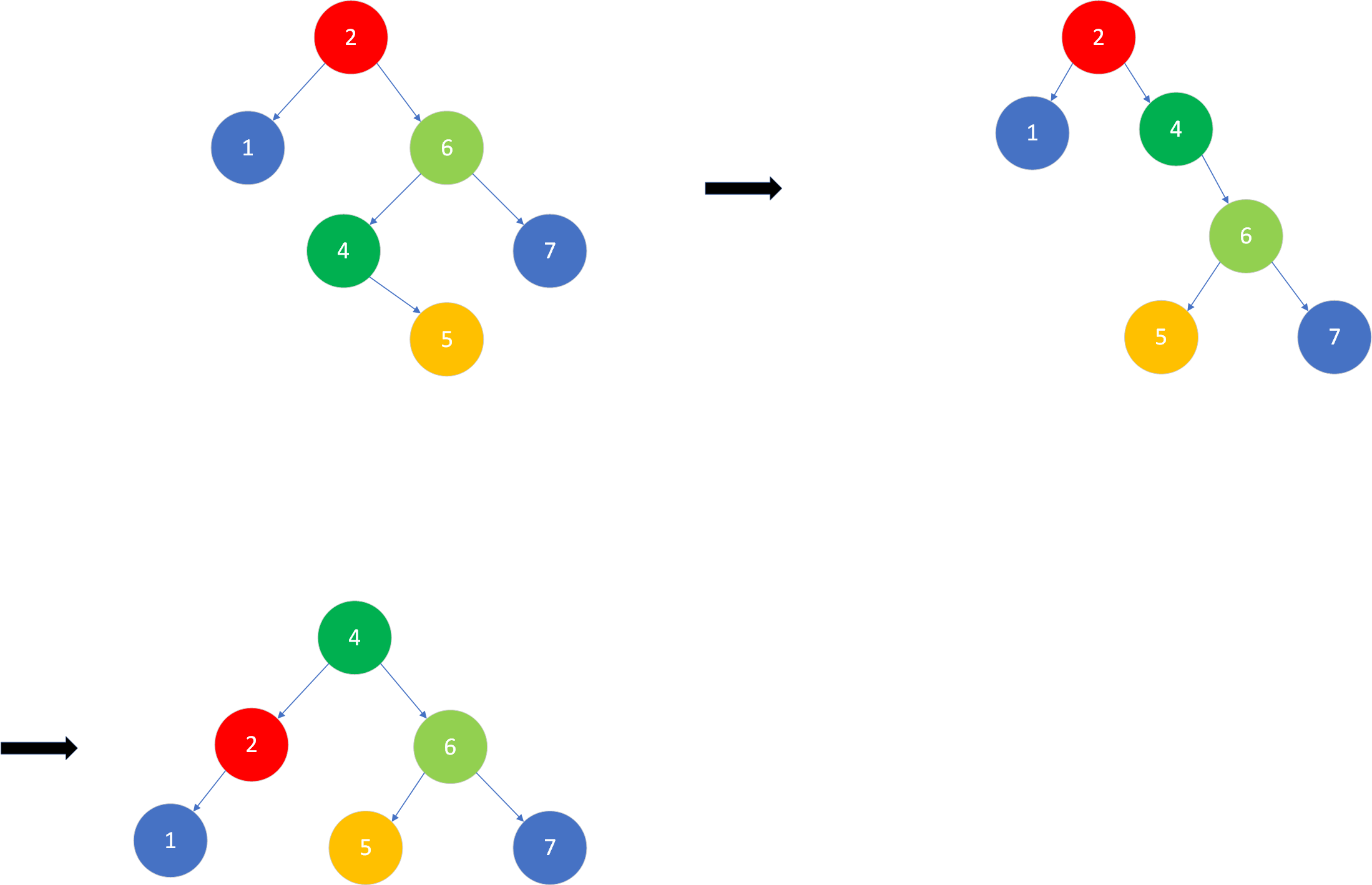
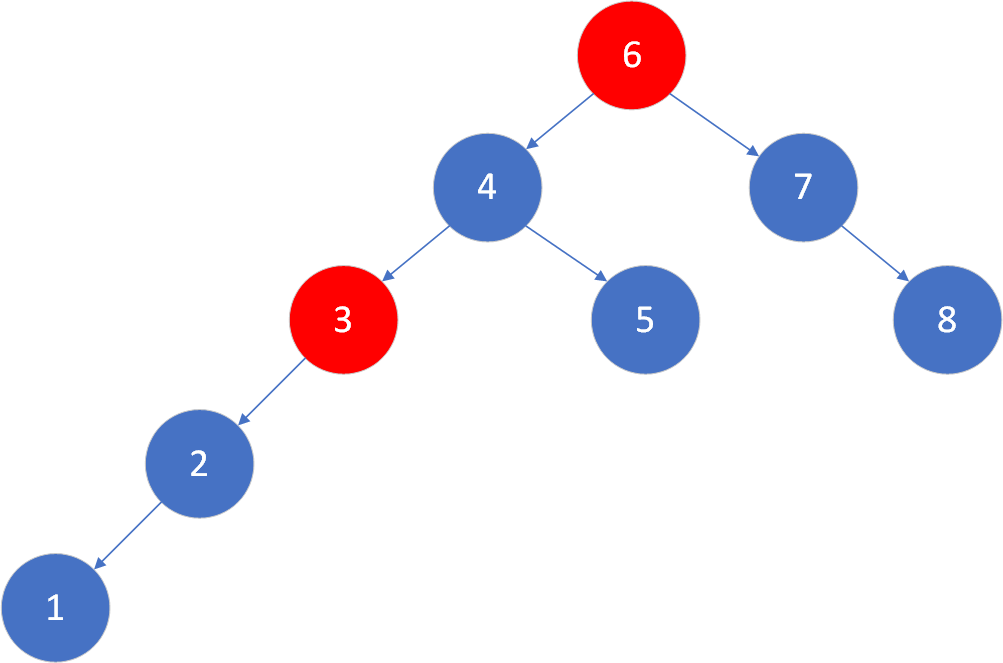
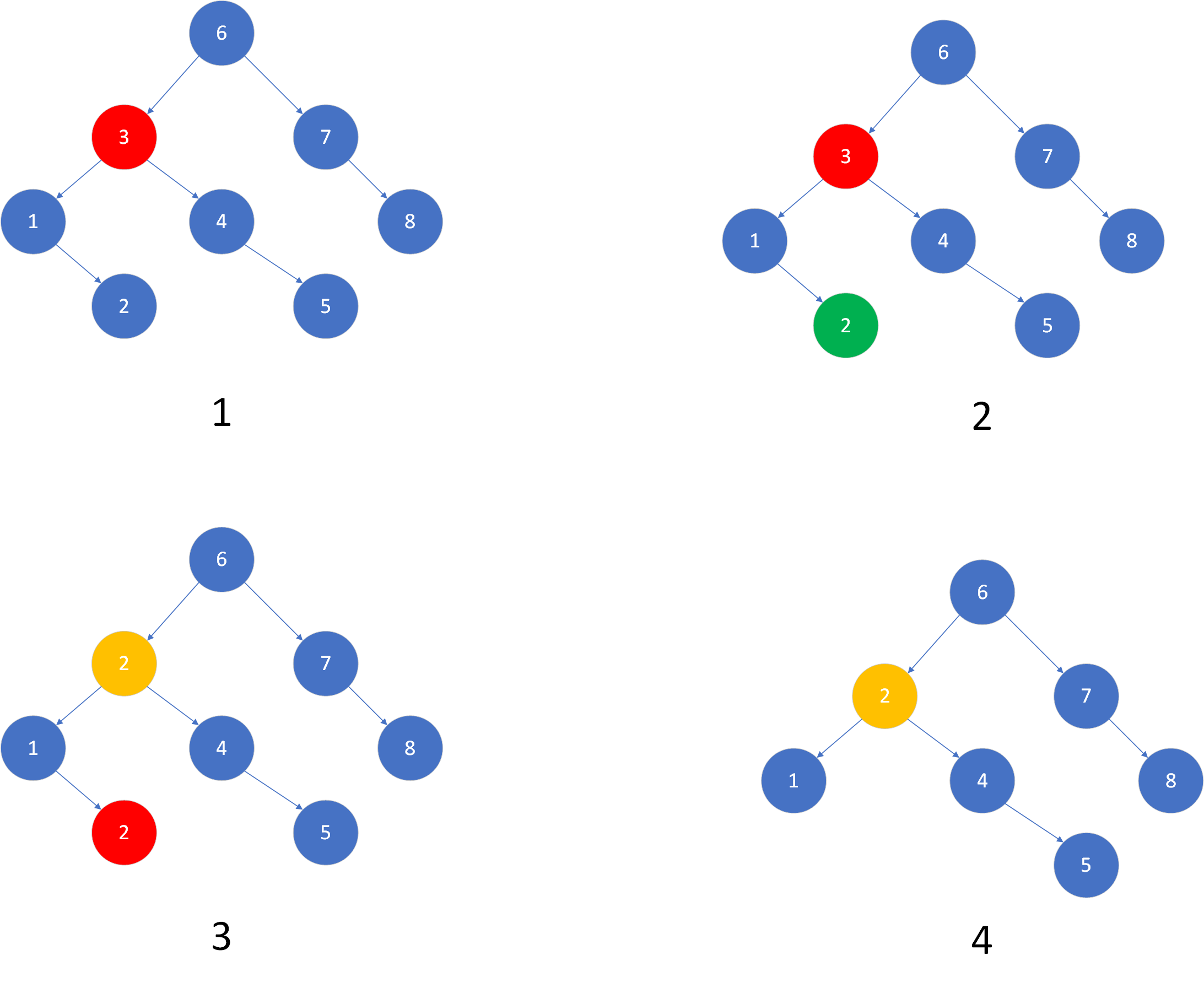
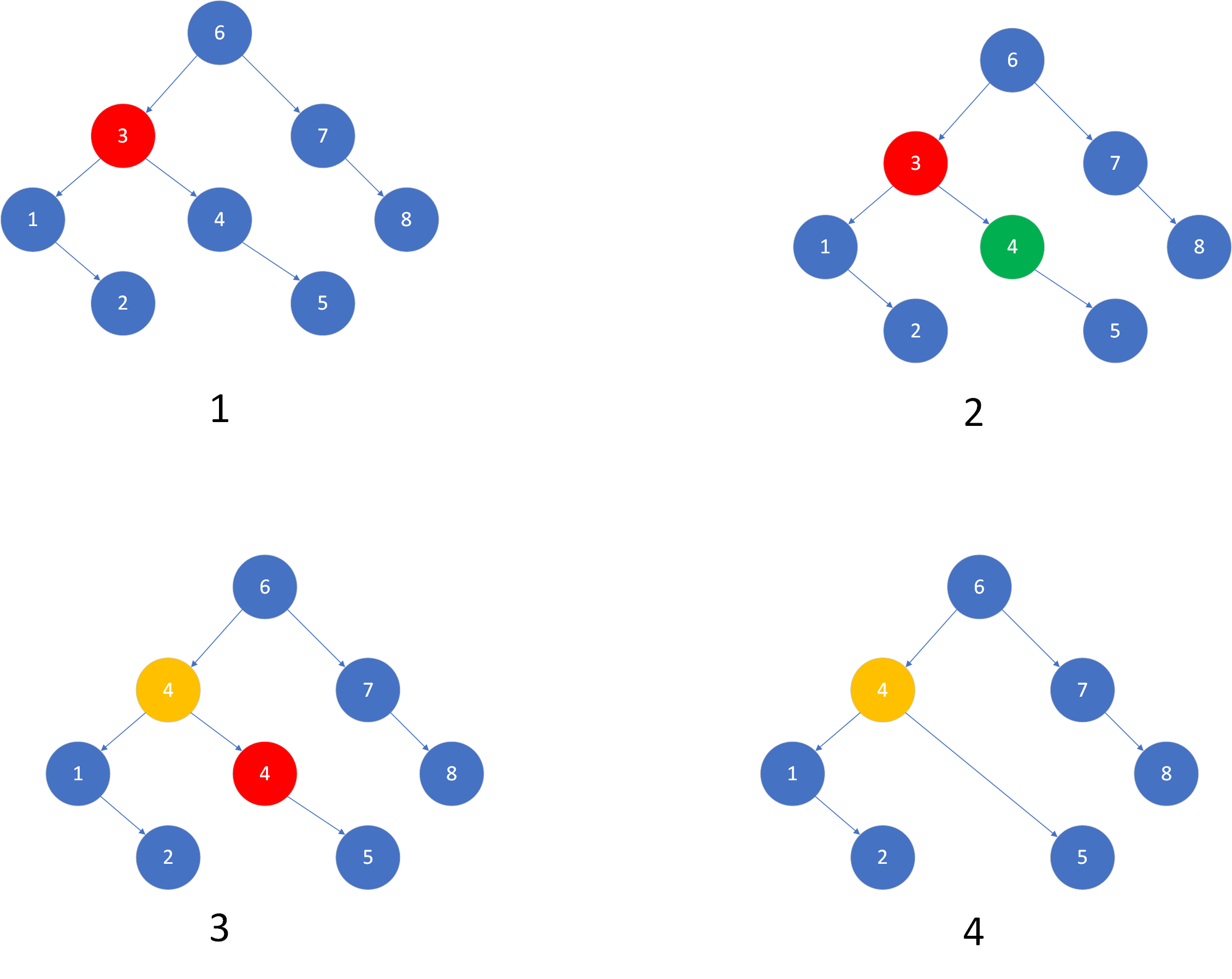
    ​ 对失衡节点的查找需要遍历树的所有节点，树中可能没有失衡节点，可能有一个，也有可能有两个。我们优先处理较低层的失衡节点。一般来说，（可能）处理较低层的失衡节点后，高层的失衡节点也随之达到了平衡。而调整高层节点，底层节点可能仍然失衡。如下图所示：多个节点失衡.png

    因此，我们希望自下而上寻找失衡节点。对于自下而上，层层遍历的操作，可借鉴层次遍历的思想。层次遍历为广度优先，考虑用队列这一数据结构实现。

    • 层次遍历：首先将根节点入队。根节点出队，将根节点存入指定“容器”，将根节点的左右孩子依次入队。队首节点出列，存入指定“容器”，将节点的左右子树依次入队。重复操作，直至队列为空。
    1. 获得按层排序的所有节点后，从容器尾开始，遍历所有节点，直到找到第一个失衡节点。
    2. 对失衡节点进行失衡类型判断，调整。
    3. 为稳妥起见，可立标志位，循环寻找失衡节点并调整，直至所有节点均为平衡节点（下述代码未实现该功能）。
    Node *FindUnbalanceNode(Node *root)
{
    MyQueue *node_queue;
    Node *nodes[MAXSIZE];
    int nodes_num = -1;
    node_queue = (MyQueue*)malloc(sizeof(MyQueue));
    
    node_queue->head = 0;
    node_queue->rear = -1;
    node_queue->length = 0;

    node_queue->nodes[++node_queue->rear] = root;
    node_queue->length++;

    while (node_queue->length > 0)
    {
        Node *tmp = node_queue->nodes[node_queue->head++];
        nodes[++nodes_num] = tmp;
        node_queue->length--;

        if ( tmp->left != NULL )
        {
            node_queue->nodes[++node_queue->rear] = tmp->left;
            node_queue->length++;
        }
        if ( tmp->right != NULL )
        {
            node_queue->nodes[++node_queue->rear] = tmp->right;
            node_queue->length++;
        }
    }
    free(node_queue);

    while ( nodes_num >= 0 )
    {
        if ( abs( GetHeight(nodes[nodes_num]->left) - GetHeight(nodes[nodes_num]->right) ) > 1 )
            return nodes[nodes_num];
        nodes_num--;
    }

    return NULL;
   
}

  • 调整

    void Adjustment(Node *unbalance_node)
{
    if ( unbalance_node != NULL )
    {
        if ( GetHeight(unbalance_node->left) > GetHeight(unbalance_node->right) )
        {
            if ( GetHeight(unbalance_node->left->left) > GetHeight(unbalance_node->left->left) )
                LLRotation(unbalance_node);
            else
                LRRotation(unbalance_node);
        }
        else
        {
            if ( GetHeight(unbalance_node->right->left) < GetHeight(unbalance_node->right->right) )
                RRRotation(unbalance_node);
            else
                RLRotation(unbalance_node);
        }
    }
}

    • L-L型调整

      ​ 关于节点的父亲的转换，自行体会。

      void LLRotation(Node *unbalance_node)
{
    Node *tmp = unbalance_node->left;
    unbalance_node->left = tmp->right;
    if ( tmp->right != NULL )
        tmp->right->parent = unbalance_node;
    tmp->right = unbalance_node;

    unbalance_node->parent->left = tmp;
    tmp->parent = unbalance_node->parent;
    unbalance_node->parent = tmp;

}

    • R-R型调整

      void RRRotation(Node *unbalance_node)
{
    Node *tmp = unbalance_node->right;
    unbalance_node->right = tmp->left;
    if ( tmp->left != NULL )
        tmp->left->parent = unbalance_node;
    tmp->left = unbalance_node;

    unbalance_node->parent->right = tmp;
    tmp->parent = unbalance_node->parent;
    unbalance_node->parent = tmp;

}

    • L-R型调整

      void LRRotation(Node *unbalance_node)
{
    RRRotation(unbalance_node->left);
    LLRotation(unbalance_node);
}

    • R-L型调整

      void RLRotation(Node *unbalance_node)
{
    LLRotation(unbalance_node->right);
    RRRotation(unbalance_node);
}

      ​ 节点中引入指向父亲的指针，不可避免地会使使用的空间增多，但在失衡节点的调整以及删除节点的操作中，指向父亲指针的引入使得操作更加简便。另外，打个比方：父亲和儿子分别住在两栋房子，因为调整，儿子搬走了，我们希望新住进来的人成为我的儿子，这显然是不对的，父子关系在人，不在房子。以L-L型失衡为例，假设失衡节点的父亲为P，失衡节点为其左孩子。若：

      Node *LLRotation(Node *unbalance_node)
{
    Node *tmp = unbalance_node->left;
    unbalance_node->left = tmp->right;
    tmp->right = unbalance_node;
    
    return tmp;
}

unbalance_node = LLRotation(unbalance_node);

      事实上，最终得到的，P的左孩子依旧为原先的左孩子，并不是新的子树的根（tmp/unbalance_node->left）。

  • 建树

    Node *CreateAVLTree(ElementType array[], int length)
{
    Node *head;
    Node *head_nonNULLChild;
    head = (Node*)malloc(sizeof(Node));
    head->element = 0;
    head->parent = NULL;

    Node *root;
    root = (Node*)malloc(sizeof(Node));
    

    root->element = array[0];
    root->left = NULL;
    root->right = NULL;
    if ( array[0] <= head->element )
    {
        head->left = root;
        head->right = NULL;
    }
    else
    {
        head->left = NULL;
        head->right = root;
    }
    
    root->parent = head;
    
    
    int i;
    for ( i = 1; i < length; i++ )
    {
        head_nonNULLChild = head->left != NULL ? head->left: head->right;
        Node *insert_node = FindNodeToBeInserted( array[i],  head_nonNULLChild);
        Insert( array[i], insert_node);

        Node *unbalance_node = FindUnbalanceNode(head_nonNULLChild);
        Adjustment(unbalance_node);
        
    }

    return head;
}

​ 查找失衡节点和调整的操作可循环直至无失衡节点。

  • 删除指定节点

    ​ 要删除指定的节点，首先要找到对应的节点，如节点不存在，则报错。

    ​ 删除的节点一般有三种类型：叶节点，只有一个孩子的节点及有两个孩子的节点。叶节点的删除十分简单，若删除节点为叶节点，直接删除即可（其父亲节点指向该节点的指针指向空指针）。只有一个孩子的节点的删除也相对容易，令其父亲节点指向该节点的指针指向其唯一的孩子，该节点指向孩子的指针置空。对于有两个孩子的节点，删除该节点后需要保证删除后的树仍满足二叉搜索树的条件：节点的所有左子孙值均小于节点值，所有右子孙值均大于节点值。实现这一条件有两种解决方法：

    1. 选择目的删除节点的左子孙的最大值替换目的删除节点值

    2. 选择目的删除节点的右子孙的最小值替换目的删除节点值

      删除2.png
      事实上，删除带两孩子的节点最后均回到删除叶子结点和删除只有一个孩子的节点这两种删除操作。对于删除带两孩子的节点，其删除为逻辑上的删除而非物理上的删除。

      代码如下：

    Node *FindNodeToBeDeleted(ElementType element, Node *root)
{
    Node *tmp = root;
    while ( tmp != NULL )
    {
        if ( tmp->element == element )
            break;
        else if ( tmp->element > element )
            tmp = tmp->left;
        else   
            tmp = tmp->right;
    }
    return tmp;
}

    void DeleteLeafNode(Node *leaf_node)
{
    Node *tmp = leaf_node->parent;
    if ( tmp->element > leaf_node->element )
        tmp->left = NULL;
    else if ( tmp->element < leaf_node->element )
        tmp->right = NULL;
    free(leaf_node);
}

    void DeleteNode(Node *delete_node)
{
    if ( delete_node->left == NULL && delete_node->right == NULL )
        DeleteLeafNode(delete_node);
    else if ( delete_node->left != NULL && delete_node->right != NULL )
    {
        Node *node_with_maxelement_of_lchild = FindNodeWithMaxElement(delete_node->left);
        delete_node->element = node_with_maxelement_of_lchild->element;
        DeleteNode(node_with_maxelement_of_lchild);
    }
    else
    {
        if ( delete_node->left != NULL )
        {
            Node *parent = delete_node->parent;
            if ( parent->left == delete_node )
                parent->left = delete_node->left;
            else
                parent->right == delete_node->left;
            delete_node->left->parent = parent;
            delete_node->left = NULL;
            free(delete_node);
        }
        else
        {
            Node *parent = delete_node->parent;
            if ( parent->left == delete_node )
                parent->left = delete_node->right;
            else
                parent->right == delete_node->right;
            delete_node->right->parent = parent;
            delete_node->right = NULL;
            free(delete_node);
        }
    }
}

    void DeleteNodeWithTargetElement(ElementType element, Node *root)
{
    Node *node_to_be_deleted = FindNodeToBeDeleted(element, root);
    DeleteNode(node_to_be_deleted);
    Node *unbalance_node = FindUnbalanceNode(root);
    Adjustment(unbalance_node);
}

    此处未保证删除一个节点进行平衡调整后所有节点均达到平衡。

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
vim(gvim)支持对齐线
输入2个正整数A，B，求A与B的最小公倍数。
软件图标变白解决方式
计算机网络-NAT配置与ACL
推荐2个在线PDF文件处理网站，功能很赞，值得关注
C#技术点
2024年最新2024网络安全入门面试必知必会_云安全面试，终于有人把网络安全程序员必学知识点全整理出来了
【ShuQiHere】在 Linux 上运行 Windows 应用的最佳工具：全面比较与选择指南
虚拟化开源服务器安装,OPENSTACK 开源虚拟化KVM，搭建部署（一）
计算机考研｜6个月准备408来得及吗？
;