图文详解一维差分

前言

一、一维差分的定义

二、一维差分的性质

三、一维差分的使用

四、ACWing 797.差分

前言

一维+二维前缀和详解

一、一维差分的定义

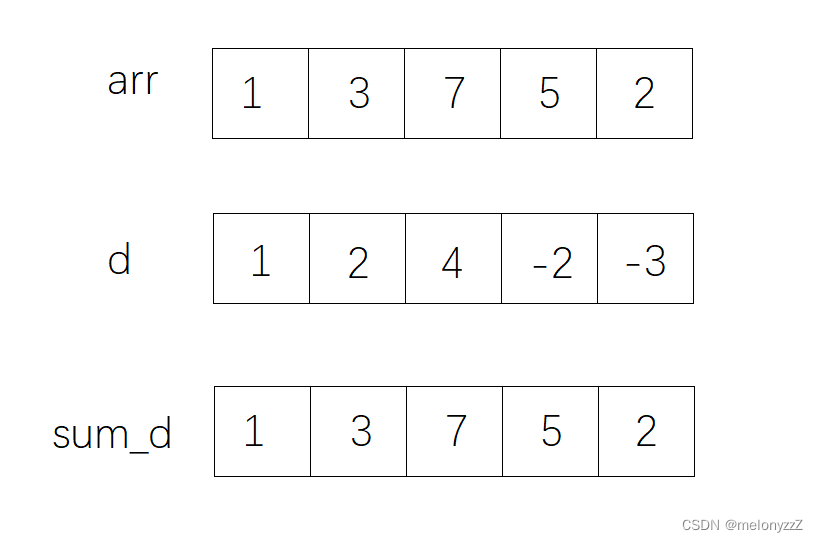
对于一个给定的一维数组 arr，它的一维差分数组 d 中 d[i] 表示数组 arr 的第 i 个元素与第 i - 1 个元素的差。用公式表示为：

① d[0] = arr[0],i == 0

② d[i] = arr[i] - arr[i - 1],i >= 1

二、一维差分的性质

一维差分数组 d 的前缀和就是一维数组 arr。

例如：

证明：

$sum_d[i] = \sum_{j=0}^{i}d_j = arr[0]+(arr[1]-arr[0])+...+(arr[i]-arr[i-1])=arr[i]$

三、一维差分的使用

一维差分的主要用处：快速地将数组 arr 的区间 [l, r] 加一个值 v。

假设：有 m 次这样的区间操作，每次操作给出 l, r 和 v。

需求：输出进行完 m 次操作后的数组 arr。

一般思路：遍历区间 [l, r] 中的所有元素并加上一个值 v，而这样的区间操作要求进行 m 次，所以时间复杂度为 O(mn)。
使用差分：使用差分可以将在数组 arr 上的"区间操作"转化为在差分数组 d 上的"单点操作"。转化方式：将数组 arr 的区间 [l, r] 加一个值 v 等价于将差分数组中的 d[l] + v，再将 d[r + 1] - v。最终的时间复杂度为 O(n + m)。

为什么可以做这样的转化？：

理解一：

将数组 arr 的区间 [l, r] 加一个值 v，数组 arr 就变成了：

$arr[0],arr[1],...,arr[l-1],arr[l]+v,arr[l+1]+v,...,arr[r]+v,arr[r+1],...,arr[n-1]$

转化为差分数组：

$d[0],d[1],...,d[l-1],d[l]+v,d[l+1],...,d[r],d[r+1]-v,...,d[n-1]$

可以看出：

d[0] 到 d[l - 1] 的值不变。
d[l] 的值加上了 v。
d[l + 1] 到 d[r] 的值不变。
d[r + 1] 的值减去了 v。
d[r + 2] 到 d[n - 1] 的值不变。

理解二：

反过来理解，如下图所示：

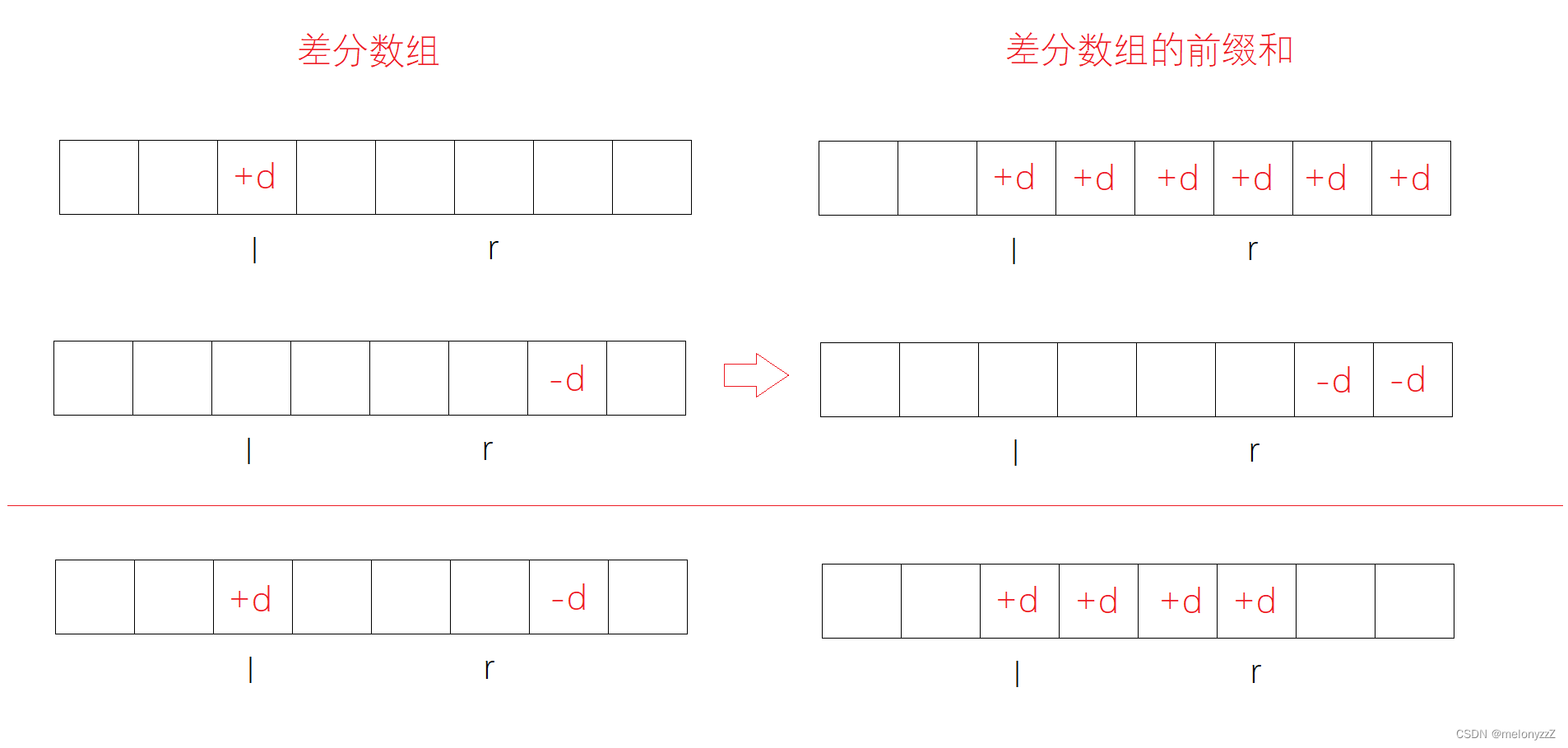
因为差分数组的前缀和相当于原数组，所以给差分数组中的 d[l] + v，再给 d[r + 1] - v 就相当于将数组 arr 的区间 [l, r] 加一个值 v。

四、ACWing 797.差分

题目描述：

输入一个长度为 n 的整数序列。接下来输入 m 个操作，每个操作包含三个整数 l，r，c，表示将序列中 [l, r] 之间的每个数加上 c。请你输出进行完所有操作后的序列。

输入格式：

第一行包括两个整数 n 和 m。

第二行包括 n 个整数，表示整数序列。

接下来 m 行，每行包括三个整数 l，r，c，表示一个操作。

输出格式：

共一行，包含 n 个整数，表示最终序列。

输入样例：

6 3
1 2 2 1 2 1
0 2 1
2 4 1
0 5 1

输出样例：

3 4 5 3 4 2

代码实现：

#include <stdio.h>

int arr[100000] = { 0 };
int d[100000] = { 0 };

int main()
{
	int n = 0;
	int m = 0;
	scanf("%d %d", &n, &m);
	int i = 0;
	for (i = 0; i < n; i++)
	{
		scanf("%d", &arr[i]);
	}
	// 初始化一维差分数组
	d[0] = arr[0];
	for (i = 1; i < n; i++)
	{
		d[i] = arr[i] - arr[i - 1];
	}
	// 进行 m 次操作
	while (m--)
	{
		int l = 0, r = 0, c = 0;
		scanf("%d %d %d", &l, &r, &c);
		d[l] += c;
		if (r < n - 1)
		{
			d[r + 1] -= c;
		}
	}
	// 计算差分数组的前缀和（即原数组 arr）并输出
	arr[0] = d[0];
	printf("%d ", arr[0]);
	for (i = 1; i < n; i++)
	{
		arr[i] = arr[i - 1] + d[i];
		printf("%d ", arr[i]);
	}
	return 0;
}