【每日力扣5】只出现一次的数字

一、题目

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1

示例 2:

输入: [4,1,2,1,2]
输出: 4

二、思路

（1）排序法

基于昨天《是否存在重复元素》的启发，这里笔者首先想到可以先将数组排序，这里花费O（NlogN）的时间，然后根据题意，除了某个元素只出现一次以外，其余每个元素均出现两次，说明那个单独的数字会与旁边两个数都不同，其他数字都会两两成对出现，也就是说，如果nums[i-1]<nums[i]<nums[i+1]，那么nums[i]就是所求解。当然还要另外先考虑只出现一次的数字是num[0]的情况。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        if (nums.size() == 1) return nums[0];//考虑仅有一个元素的退化情况
        sort(nums.begin(),nums.end());//给数组排序
        if(nums[0] < nums[1])//先考虑第一个元素nums[0]仅出现一次的情况
        {
            if(nums[1] == nums[2])
                return nums[0];
            else
                return nums[1];
        }
        else
            for(int i = 1; i < nums.size() - 1; i++)//从nums[1]开始搜索全数组
                if((nums[i] > nums[i-1])&&(nums[i] < nums[i+1]) )//当出现nums[i-1]<nums[i]<nums[i+1]
                    return nums[i]; //那么nums[i]便是所求解
        return nums[nums.size() - 1];//emmm本来到这里所有情况都考虑到，前文已经都写了return语句的，但是为了通过编译器，便在这里加上一句
    }
};

经分析，时间复杂度为O(NlogN)（来自于排序）

空间复杂度为O(logN)（来自于排序）

（2）哈希表（使用set容器）

受昨天的哈希表法的启发，这道题也可以使用哈希法引入set集合求解，但是会有额外空间消耗

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int n = nums.size();
        unordered_set<int> s;//声明一个set
        for(int x : nums)//遍历数组nums[]，对于每一个元素x
        {
            if(s.find(x)!=s.end())//如果set中已经存在x
                s.erase(x);//删除x
            else//如果set中未存在x
                s.insert(x);//插入x
        }
        return *s.begin();//最终set中剩下的唯一元素便是数组nums[]中的仅出现一次的元素
    }
};

通过了，但果然结果不尽人意。

三、官方解法

位运算！（异或运算）

对于这道题，可使用异或运算⊕。异或运算有以下三个性质。

任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a。
任何数和其自身做异或运算，结果是 0，即 a⊕a=0。
异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

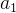
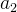
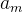
假设数组中有2m+1 个数，其中有 m 个数各出现两次，一个数出现一次。令 $a_{1}$ ， $a_{2}$ ，...， $a_{m}$ 为出现两次的 m 个数， $a_{m+1}$ 为出现一次的数。根据性质 3，数组中的全部元素的异或运算结果总是可以写成如下形式：

$(a_{0}\bigoplus a_{0})\bigoplus(a_{1}\bigoplus a_{1})\bigoplus(...)\bigoplus(a_{m}\bigoplus a_{m})\bigoplus a_{m+1}$

根据性质 2 和性质 1，上式可化简和计算得到如下结果：

$0\bigoplus0\bigoplus0\bigoplus...\bigoplus a_{m+1} = a_{m+1}$

因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret = 0;
        for (auto e: nums) ret ^= e;
        return ret;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/single-number/solution/zhi-chu-xian-yi-ci-de-shu-zi-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析

时间复杂度：O(n)，其中 n 是数组长度。只需要对数组遍历一次。
空间复杂度：O(1)。

四、学习心得

位运算：一种可以巧妙利用数组各元素间数值逻辑关系的方法，不花费额外空间！