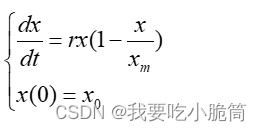一、问题
1、史教授讲授三个班的计算机课程,需要在期末考试中审阅120份考卷,史教授有2个研究生助手,小德和小华审阅期末考卷,所有试卷必须在3天内审阅完毕并公布分数,在这段时间内,小德有12h,小华有10h审阅试卷,小德每审阅一份试卷平均需要7.2min, 小华每审阅一份试卷平均需要12min, 但小德审阅的试卷有10%需要史教授重审,小华审阅的试卷有6%需要重审,那么每个研究生助手分配多少份试卷,可以使史教授重审量最少?
(1)构建规划模型;
(2)求解该规划模型;
(3)如果史教授可以让小德或小华多工作1h,应该选择谁?这1h会有怎样的影响?
2、某工厂有4名操作工可以被指派到4台机器上工作,下表显示了每名工人在每台机器上生产一件产品所需的时间,请制定最优指派方案,并计算总时间的最小值。
| 操作工 | 机器A | 机器B | 机器C | 机器D |
| 1 | 10 | 12 | 9 | 11 |
| 2 | 5 | 10 | 7 | 8 |
| 3 | 12 | 14 | 13 | 11 |
| 4 | 8 | 15 | 11 | 9 |
3、某企业经营两种商品,第一种商品每吨售价30元,第二种商品每吨售价450元。每售出一吨第一种商品所需要的营业时间平均是0.5h,每售出一吨第二种商品所需要的营业时间平均是(2+0.25
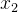
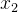
4、以x(t)表示时刻t的人口,下面是阻滞增长(Logistic)模型:
试解释模型中涉及的所有变量、参数,并简洁表述该模型的建模思想,什么时候人口增长速度最快。
5、新型冠状病毒肺炎的防控
2019年底,新型冠状病毒肺炎(Corona Virus Disease 2019,COVID-19)疫情突然爆发,世界各国人民的生命健康和经济发展受到极大的影响和威胁。虽然各国都出台了一系列的疫情防控措施,但由于国情和民众认同不同等多种因素的影响,导致防控效果有较大的差异。
“群防群控”是控制病毒传播的有效措施,会在短时间内切断病毒的传播途径,但会以经济停滞和人民失业为代价。而欧美某些国家遵循“群体免疫”的策略,通过适当措施“缓和”病毒传播的速度,而不采用封城的措施。采用何种策略需要充分考量病毒本身的传播特征。
请结合全球新型冠状病毒肺炎疫情数据,建立数学模型解决下述问题:选取合理的评价指标,建立数学模型对世界范围内主要国家抗击疫情的效果进行综合评价。
二、解决方案
问题一
(1)构建规划模型;
决策变量:设小德批阅x1份试卷,小华批阅x2份试卷
目标函数:小德重审0.1*x1份,小华重审0.06*x2份
总共重审min=0.1*x1+0.06*x2份
约束条件: x1+x2>=120
0.12*x1<=12;
0.2*x2<=10;
0.12*x1+0.2*x2<=72;
x1,x2>=0;
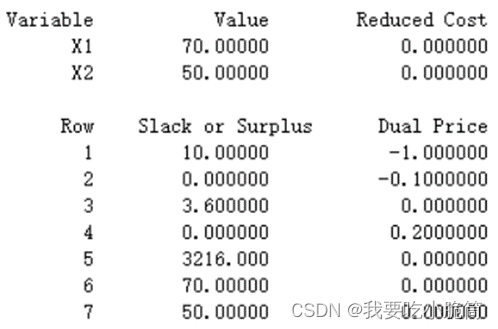
(2)求解该规划模型;
min=0.1*x1+0.06*x2;
x1+x2>=120;
0.12*x1<=12;
0.2*x2<=10;
7.2*x1+12*x2<=4320;
x1>0;
x2>0;
end
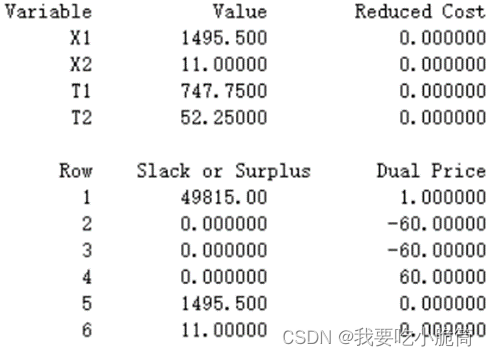
由敏感度分析,最佳应是小德70份,小华50份
答:这一小时应该增加在小华上面,会减少0.2h的重审时间。
问题二
(1)模型建立
Cij~操作工i指派到j机器上工作所用的时间
| 操作工 | j=1 | j=2 | j=3 | j=4 |
| i=1 | 10 | 12 | 9 | 11 |
| i=2 | 5 | 10 | 7 | 8 |
| i=3 | 12 | 14 | 13 | 11 |
| i=4 | 8 | 15 | 11 | 9 |
若选择操作工i在j机器上工作,则ci=0表示不在i机器工作,ci=1表示在i机器工作;
(2)LINGO代码
MODEL:
sets:
person/1..4/;
machine/1..4/;
link(person, machine): c, x;
endsets
data:
c= 10, 12, 9, 11,
5, 10, 7, 8,
12,14,13,11,
8,15,11,9;
enddata
min=@sum(link: c*x);
@for(person(i): @sum(machine (j):x(i,j))<=1;);
@for(machine (i):@sum(person(j):x(j,i))=1;);
@for(link: @bin(x));
END
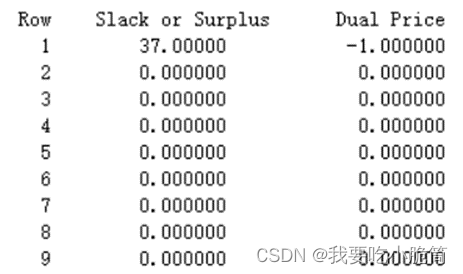
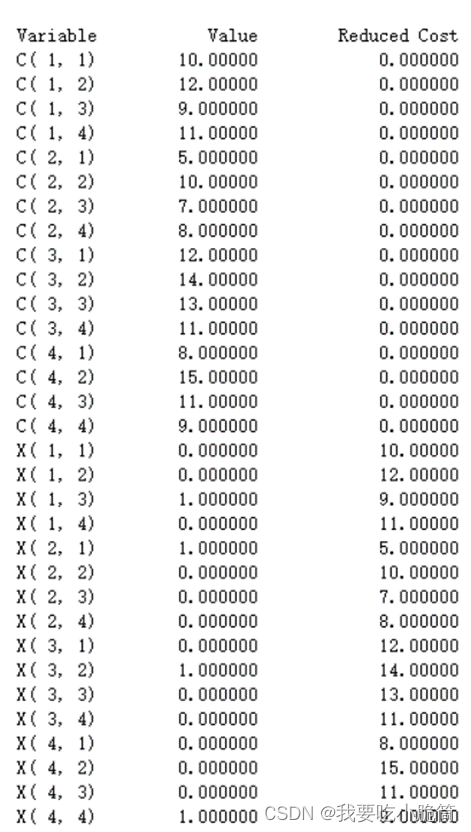
得x13=x21=x32=x44=1,其他变量为0
操作工1~C,2~A,3~B,4~D
总时间为37
问题三
(1)模型建立
设第一种商品出售吨数为x1,第一种商品出售吨数为x2
第一种商品时间为t1,第一种商品时间为t2,
max=30*x1+450*x2;
0.5*x1+2*x2+0.25*x2*x2=800;
x1>0;
x2>0;
(2)LINGO代码
max=30*x1+450*x2;
t1=0.5*x1;
t2=2*x2+0.25*x2^2;
t1+t2=800;
x1>0;
x2>0;
end
X1=1495t,x2=11t时其营业额最大。
问题四
(1)解释
r(x)为人口年增长率,是关于x的线性函数
(2)建模思想
人数增长到一定数量后增长率会因为资源环境等因素而下降,且其产生的阻滞作用随人口增加而变大,所以r为x的减函数
问题五
参考数据百度疫情实时大数据报告https://voice.baidu.com/act/newpneumonia/newpneumonia/
| 国家 | 新增 | 累计 | 治愈 | 死亡 |
| 中国 | 56632 | 3947734 | 296512 | 20102 |
| 50007 | 88244870 | 84040477 | 1038900 | |
| 9796 | 43334657 | 42725055 | 524903 | |
| 51925 | 31824220 | 30492176 | 669436 | |
| 101957 | 30276632 | 29396235 | 149162 | |
| 122597 | 27334463 | 26306700 | 140357 | |
| 52855 | 22525358 | 22095052 | 179706 | |
| 2500 | 18406485 | 17832604 | 380643 | |
| 9283 | 18298341 | 18129388 | 24474 | |
| 16905 | 17959329 | 17191557 | 167842 | |
| 0 | 15085742 | 14986340 | 98996 | |
| 0 | 12613634 | 12130469 | 107604 | |
| 748 | 10738909 | 9617180 | 43083 | |
| 28039 | 9341492 | 9108218 | 129016 | |
| 15376 | 9176092 | 8992743 | 31063 | |
| 31562 | 7887810 | 7664642 | 9507 |
设其中新增为x1,累计为x2,治疗x3,死亡x4,数据导入
(1)R型聚类分析
可以看出某些指标之间可能存在较强的相关性。为了验证想法,用matlab计算4个指标之间的相关系数
matlab代码:
clc, clear
a=load('yq.txt');
b=zscore(a);
r=corrcoef(b)
%d=tril(1-r); d=nonzeros(d)';
d=pdist(b','correlation');
z=linkage(d,'average');
h=dendrogram(z);
set(h,'Color','k','LineWidth',1.3)
T=cluster(z,'maxclust',3)
for i=1:3
tm=find(T==i);
tm=reshape(tm,1,length(tm));
fprintf('第%d类的有%s\n',i,int2str(tm));
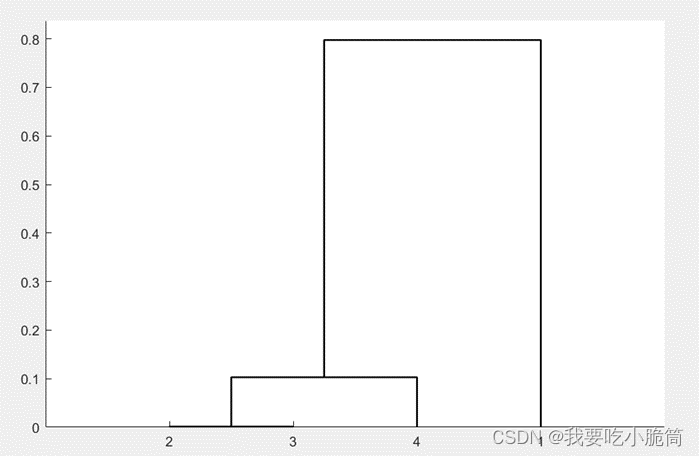
end由聚类图看出,累计人数、治愈人数和死亡人数首先被分到了一起,说明具有较大的相关性。将其分为3类,则可以从x1新增X2累计X4死亡三个指标进行分析
(2)Q类型分析
matlab代码:
clc,clear
load yq.txt %把原始数据保存在纯文本文件gj.txt中
yq(:,3)=[]; %删除数据矩阵的第3列~第6列,即使用变量1,2,7,8,9,10
yq=zscore(yq); %数据标准化
y=pdist(yq); %求对象间的欧氏距离,每行是一个对象
z=linkage(y,'average'); %按类平均法聚类
h=dendrogram(z); %画聚类图
set(h,'Color','k','LineWidth',1.3) %把聚类图线的颜色改成黑色,线宽加粗
for k=3:5
fprintf('划分成%d类的结果如下:\n',k)
T=cluster(z,'maxclust',k); %把样本点划分成k类
for i=1:k
tm=find(T==i); %求第i类的对象
tm=reshape(tm,1,length(tm)); %变成行向量
fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
end
if k==5
break
end
fprintf('**********************************\n');
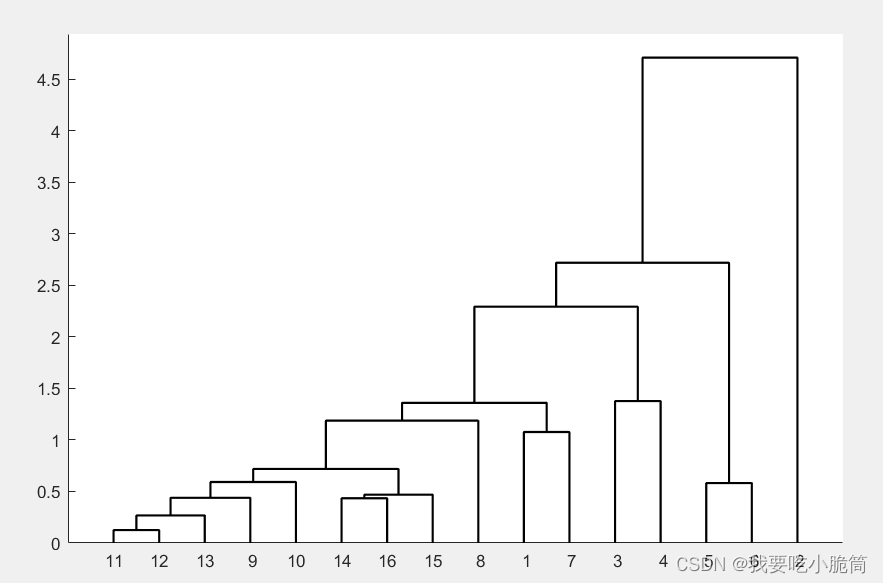
end划分成3类的结果如下:
第1类的有5 6
第2类的有1 3 4 7 8 9 10 11 12 13 14 15 16
第3类的有2
**********************************
划分成4类的结果如下:
第1类的有1 7 8 9 10 11 12 13 14 15 16
第2类的有3 4
第3类的有5 6
第4类的有2
**********************************
划分成5类的结果如下:
第1类的有3
第2类的有4
第3类的有1 7 8 9 10 11 12 13 14 15 16
第4类的有5 6
第5类的有2
由此可以看出美国的防疫与其他国家大不相同,其主要表现为累计人数和死亡人数大不相同
(3)主成分分析
matlab代码:
clc,clear
load yq.txt %把原始数据保存在纯文本文件gj.txt中
gj=zscore(yq); %数据标准化
r=corrcoef(yq); %计算相关系数矩阵
%下面利用相关系数矩阵进行主成分分析,vec1的列为r的特征向量,即主成分的系数
[vec1,lamda,rate]=pcacov(r) %lamda为r的特征值,rate为各个主成分的贡献率
contr=cumsum(rate) %计算累积贡献率
f=repmat(sign(sum(vec1)),size(vec1,1),1);%构造与vec1同维数的元素为±1的矩阵
vec2=vec1.*f %修改特征向量的正负号,使得每个特征向量的分量和为正
num=4; %num为选取的主成分的个数
df=yq*vec2(:,1:num); %计算各个主成分的得分
tf=df*rate(1:num)/100; %计算综合得分
[stf,ind]=sort(tf,'descend'); %把得分按照从高到低的次序排列
tf=tf',stf=stf', ind=ind'运行出结果后对参数估计,可以选择一部分重要再丢掉一部分。
注:matlab代码和txt要放在一个文件夹下