树链剖分学习笔记

前言

树链剖分这个东西呢，简而言之就是把一些树上的操作转换成线性的问题。那看起来平平无奇的树链剖分，为什么很多人就是喜欢使用他呢，那想必肯定是有原因的，我们先卖个关子，先看一下树链剖分怎么写，原理是什么。

前置芝士

线段树
树形dp
dfs序
如果不会可以看往期的学习笔记

算法详解

树链剖分的话我们就讲个一道模版题，毕竟也是一种方法，可以选择性使用。

洛谷模板 P3384

如题，已知一棵包含 $N$ 个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

1 x y z，表示将树从 $x$ 到 $y$ 结点最短路径上所有节点的值都加上 $z$ 。
2 x y，表示求树从 $x$ 到 $y$ 结点最短路径上所有节点的值之和。
3 x z，表示将以 $x$ 为根节点的子树内所有节点值都加上 $z$ 。
4 x 表示求以 $x$ 为根节点的子树内所有节点值之和

概念简介

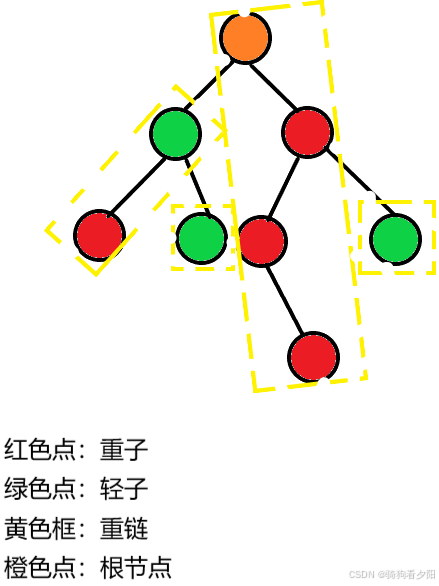
首先，因为后面在讲解的时候会涉及到一些名词，我们来解释一下。

重子：对于每一个非叶子节点，它的儿子中以那个儿子为根的子树节点数最大的儿子为该节点的重子。
轻子：跟重子相反，一个点不是重子就是轻子（叶子节点除外），对于每一个非叶子节点，它的子中非重儿子的剩下所有儿子即为轻子。
重边：一个父亲连接他的重子的边称为重边。
轻边：跟重边相反，每一条边不是重边就是轻边。
重链：重链的要求非常难，一点是相邻的重边连起来一个重子的链就是重链。
如果有还不理解的同学，我们来画一张图来找一找这些东西在哪里。

需要的函数

第一个dfs

这个dfs他到底要解决什么问题呢？其实有这么用处。

标记每一个点的深度
预处理出每一个点的父亲
标记每个非叶子节点的子树大小(含它自己)
标记每个非叶子节点的重儿子编号son[]

void dfs1(int x,int f,int deep)
{//x当前节点，f父亲，deep深度 
	dep[x]=deep;//标记每个点的深度 
	fa[x]=f;//标记每个点的父亲 
	siz[x]=1;//标记每个非叶子节点的子树大小 
	int maxn=-1;//记录重儿子的儿子数 
	for(int i=beg[x];i;i=nex[i])
	{
		int y=to[i];
		if(y==f)
			continue;//若为父亲则continue 
		dfs1(y,x,deep+1);//dfs其儿子 
		siz[x]+=siz[y];//把它的儿子数加到它身上 
		if(siz[y]>maxn)
			son[x]=y,maxn=siz[y];//标记每个非叶子节点的重儿子编号 
	}
}

第二个dfs

第二个dfs的目的其实跟第一个是差不多的，同样是预处理，我们先列出来看看。

标记每个点的新编号
赋值每个点的初始值到新编号上
处理每个点所在链的顶端
处理每条链

void dfs2(int x,int topf){//x当前节点，topf当前链的最顶端的节点 
	id[x]=++cnt;//标记每个点的新编号 
	wt[cnt]=w[x];//把每个点的初始值赋到新编号上来 
	top[x]=topf;//这个点所在链的顶端 
	if(!son[x])
		return;//如果没有儿子则返回 
	dfs2(son[x],topf);//按先处理重儿子，再处理轻儿子的顺序递归处理 
	for(int i=beg[x];i;i=nex[i])
	{
		int y=to[i];
		if(y==fa[x]||y==son[x])
			continue;
		dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链 
	}
}

树剖部分

敲一下黑板，这是最重要的部分，因为第二个dfs的便利顺序是先重子，再轻子，然后就不难得到一个很有用的东西：

因为顺序是先重再轻，所以每一条重链的新编号是连续的
因为是dfs，所以每一个子树的新编号也是连续的
然后我们搬出题目让我们干的事情，一件一件分析：
处理任意两点间路径上的点权和
处理一点及其子树的点权和
修改任意两点间路径上的点权
修改一点及其子树的点权

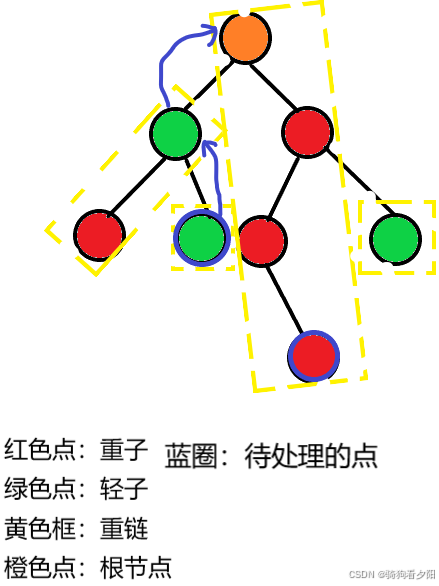
处理任意两点间路径时：
设所在链顶端的深度更深的那个点为 $x$ 点 $an s$ 加上 $x$ 点到 $x$ 所在链顶端这一段区间的点权和，把 $x$ 跳到 $x$ 所在链顶端的那个点的上面一个点。可能会有一点点抽象，我们画一个图帮助理解一下。
那么好的，在分析一下，因为这先序号都是连续的，所以怎么维护呢，可以使用线段树，不会的可以翻往期的笔记。时间复杂度就是 $O\left(\log^2n\right)$

inline int qRange(int x,int y){
	int ans=0;
	while(top[x]!=top[y]){//当两个点不在同一条链上 
		if(dep[top[x]]<dep[top[y]])swap(x,y);//把x点改为所在链顶端的深度更深的那个点
		res=0;
		query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
		ans+=res;
		ans%=mod;//按题意取模 
		x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
	}
	//直到两个点处于一条链上
	if(dep[x]>dep[y])
		swap(x,y);//把x点深度更深的那个点
	res=0;
	query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可
	ans+=res;
	return ans%mod;
}

处理一点及其子树的点权和：想到记录了每个非叶子节点的子树大小(含它自己)，并且每个子树的新编号都是连续的,直接线段树区间查询即可，时间复杂度 $O\left(\log n\right)$

inline int qSon(int x){
	res=0;
	query(1,1,n,id[x],id[x]+siz[x]-1);//子树区间右端点为id[x]+siz[x]-1 
	return res;
}

下面是区间修改的，跟查询基本一样：

inline void updRange(int x,int y,int k){
	k%=mod;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		update(1,1,n,id[top[x]],id[x],k);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	update(1,1,n,id[x],id[y],k);
}

inline void updSon(int x,int k){
	update(1,1,n,id[x],id[x]+siz[x]-1,k);
}

建树

普通的线段树，不多说了。

代码部分

#include<bits/stdc++.h>
using namespace std;
#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define len (r-l+1)
const int maxn=200000+10;
int n,m,r,mod;//见题意 
int e,beg[maxn],nex[maxn],to[maxn],w[maxn],wt[maxn];//链式前向星数组，w、wt初始点权数组 
int a[maxn<<2],laz[maxn<<2];//线段树数组、lazy懒标记 
int son[maxn],id[maxn],fa[maxn],cnt,dep[maxn],siz[maxn],top[maxn];//son重子编号,id新编号,fa父亲节点,cnt dfs_clock/dfs序,dep深度,siz子树大小,top当前链顶端节点
int res;
void add(int x,int y){//链式前向星加边 
    to[++e]=y;
    nex[e]=beg[x];
    beg[x]=e;
}
//线段树操作，不多说了，看往期笔记 
void pushdown(int rt,int lenn)
{
	laz[rt<<1]+=laz[rt];
	laz[rt<<1|1]+=laz[rt];
    a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
    a[rt<<1|1]+=laz[rt]*(lenn>>1);
    a[rt<<1]%=mod;
    a[rt<<1|1]%=mod;
    laz[rt]=0;
}
void build(int rt,int l,int r)
{
    if(l==r){
        a[rt]=wt[l];
        if(a[rt]>mod)a[rt]%=mod;
        return;
    }
    build(lson);
    build(rson);
    a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
}
void query(int rt,int l,int r,int L,int R)
{
	if(L<=l&&r<=R)
	{
		res+=a[rt];
		res%=mod;
		return;
	}
	else
	{
		if(laz[rt])
			pushdown(rt,len);
		if(L<=mid)
			query(lson,L,R);
		if(R>mid)
			query(rson,L,R);
	}
}
void update(int rt,int l,int r,int L,int R,int k)
{
    if(L<=l&&r<=R)
	{
		laz[rt]+=k;
		a[rt]+=k*len;
	}
	else
	{
		if(laz[rt])
			pushdown(rt,len);
		if(L<=mid)
			update(lson,L,R,k);
		if(R>mid)
			update(rson,L,R,k);
		a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
	}
} 
int qRange(int x,int y)
{
	int ans=0;
	while(top[x]!=top[y])//当两个点不在同一条链上
	{ 
		if(dep[top[x]]<dep[top[y]])
			swap(x,y);//把x点改为所在链顶端的深度更深的那个点
		res=0;
		query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
		ans+=res;
		ans%=mod;//按题意取模 
		x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
	}
	//直到两个点处于一条链上，跟LCA类似 
	if(dep[x]>dep[y])
		swap(x,y);//把x点深度更深的那个点
	res=0;
	query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可
	ans+=res;
	return ans%mod;
}
void updRange(int x,int y,int k)//同上 
{
	k%=mod;
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]])
			swap(x,y);
		update(1,1,n,id[top[x]],id[x],k);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	update(1,1,n,id[x],id[y],k);
}
int qSon(int x)
{
	res=0;
	query(1,1,n,id[x],id[x]+siz[x]-1);//子树区间右端点为id[x]+siz[x]-1 
	return res;
}
void updSon(int x,int k){//同上 
	update(1,1,n,id[x],id[x]+siz[x]-1,k);
}
void dfs1(int x,int f,int deep){//x当前节点，f父亲，deep深度 
	dep[x]=deep;//标记每个点的深度 
	fa[x]=f;//标记每个点的父亲 
	siz[x]=1;//标记每个非叶子节点的子树大小 
	int maxson=-1;//记录重儿子的儿子数 
	for(int i=beg[x];i;i=nex[i])
	{
		int y=to[i];
		if(y==f)
			continue;//若为父亲则continue 
		dfs1(y,x,deep+1);//dfs其儿子 
		siz[x]+=siz[y];//把它的儿子数加到它身上 
		if(siz[y]>maxson)
			son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号 
	}
}

void dfs2(int x,int topf){//x当前节点，topf当前链的最顶端的节点 
	id[x]=++cnt;//标记每个点的新编号 
	wt[cnt]=w[x];//把每个点的初始值赋到新编号上来 
	top[x]=topf;//这个点所在链的顶端 
	if(!son[x])
		return;//如果没有儿子则返回 
	dfs2(son[x],topf);//按先处理重儿子，再处理轻儿子的顺序递归处理 
	for(int i=beg[x];i;i=nex[i])
	{
		int y=to[i];
		if(y==fa[x]||y==son[x])
			continue;
		dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链 
	}
}
int main()
{
    cin>>n>>m>>r>>mod; 
    for(int i=1;i<=n;i++)
		cin>>w[i];
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        add(u,v);
		add(v,u);
    }
    dfs1(r,0,1);
    dfs2(r,r);
    build(1,1,n);
	while(m--)
	{
        int k,x,y,z;
        cin>>k;
        if(k==1)
		{
            cin>>x>>y>>z;
            updRange(x,y,z);
        }
        else if(k==2)
		{
            cin>>x>>y;
            printf("%d\n",qRange(x,y));
        }
        else if(k==3)
		{
            cin>>x>>y;
            updSon(x,y);
        }
        else
		{
            cin>>x;
            printf("%d\n",qSon(x));
    	}
    }
}