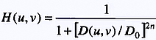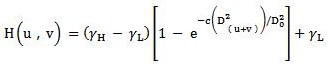1、主要步骤:空域(傅里叶变换、卷积)>>>频域(与转移函数相乘、处理、傅里叶反变换)>>>空域
2、常用频域增强方法:
巴特沃斯滤波器:阶为n,截断频率为D0的转移函数为:
(1)低通滤波:
低通巴特沃斯滤波器在高低频率间的过渡比较光滑,所以得到的输出图其“振铃”现象不明显。
频域低通滤波器能消除虚假轮廓。
(2)高通滤波:就是利用滤波器的频率特性,让高频的通过,低频的无法通过,就好比在频率域设置阈值,频率域每一个频率分量有一个“幅值”,滤波器就好比在不同的频率分量给这个幅值乘以不同的增益,高通就好比高频部分增益为1,低频部分增益为0,当然这是理想高通。高斯高通滤波器就是频域每一个频率分量的增益的连接而成的曲线是一个高斯曲线
高通巴特沃斯滤波器.
G( x, y ) = g ( x, y ) + c * f( x, y ) c = 0.5,0<=c<=1
(3)带通和带阻滤波
带阻滤波器:阻止一定频率范围内的信号通过而允许其他频率范围内的信号通过。
带通滤波器:允许一定频率范围内的信号通过而阻止其它频率范围内的信号通过。带通和带阻互补。
低通、高通、带通、带阻等线性滤波器可以较好地消除线性叠加在图像上的加性噪声。但实际中,噪声和图像也常常是以非线性的方式结合。例如光源照明成像的情况,其中光的入射和景物的反射是以相乘的形式对成像做出贡献的,这样成像中的噪声与景物也是相乘的关系。
同态滤波:
是一种在频域中同时将图像亮度范围进行压缩和将图像对比度进行增强的方法。
f(x, y) = i(x, y) r(x, y)(一幅图像可以看做是 照度分量和反射分量的乘积)
ln f(x, y) = ln i(x, y) + ln r(x, y)(为了分开处理,两边分别取对数)
cvLog(ImgLog, ImgLog);
F(u, v) = I(u, v) + R(u, v) (傅里叶变换)
cvDFT(Fourier, Fourier, CV_DXT_FORWARD);
H(u, v)F(u, v) = H(u, v)I(u, v) + H(u, v)R(u, v) (H(u, v)同态滤波函数,可分别作用在照度分量上和反射分量上)
cvMul(ImageRe,matH,ImageRe);
cvMul(ImageIm,matH,ImageIm);
hf (x,y) = hi (x,y)+ hr (x,y) (反变换)
cvDFT(Fourier, Fourier, CV_DXT_INV_SCALE);
cvSplit(Fourier,ImageRe, ImageIm, 0, 0);
g(x,y)=exp|hf (x,y)|=exp|hi (x,y)|exp|hr (x,y)|(前面去对数,在转变回来)
cvExp(ImageRe, ImageRe);
cvExp(ImageIm, ImageIm);
cvMul(ImageRe, ImageIm, ImgDst);
最后归一化,显示。
同态滤波消噪过程:先利用非线性的对数变换将乘性噪声转化为加性噪声,然后就可用线性滤波器进行消除,最后再进行非线性的指数反变换以获得原始的无噪声图像。
同态滤波处理的流程如下:
S(x,y)——>Log—->FFT—->高通滤波—->IFFT—->Exp—->T(x,y)
其中S(x,y)表示原始图像;T( x,y)表示处理后的图像;Log 代表对数运算;FFT 代表傅立叶变换;IFFT 代表傅立叶逆变换;Exp 代表指数运算。
因为一般照度分量在空间变化较缓慢,而反射分量在不同物体交界处会急剧变化,所以图像对数的傅里叶变换后的低频部分主要对应照度分量,而高频部分对应反射分量。
这样我们可以设计一个对傅里叶变换结果的高频和低频分量影响不同的滤波函数H(u,v)。
高斯型高通滤波器修改形式:
式中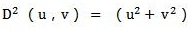
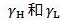
OpenCV中,构造高斯型高通滤波器:
CvMat *matH = cvCreateMat( height, width, CV_32FC1);
HPF( matH );
void HPF(CvMat *matH, float D0 = 10,float rH = 2.0,float rL = 0.3,float c = 0)
{
if (D0 < 0){
qDebug()<<"ERROR!";
return ;
}
for (int u = 0; u < matH->rows; ++u)
for (int v =0 ;v < matH->cols; ++v){
float D = (u * u )+(v * v);
*( (float*)CV_MAT_ELEM_PTR(*matH, u, v) ) =
(rH - rL)*( 1 - exp(-(c * D * D)/(D0*D0)) ) + rL;//高斯型高斯滤波器
}
}
》》》下文摘自:http://course.cug.edu.cn/rs/COURSE/6-3-4-a.HTM《《《
同态滤波增强是把频率过虑和灰度变换结合起来的一种处理方法。它是把图像的照明反射模型作为频域处理的基础,利用压缩灰度范围和增强对比度来改善图像的一种处理技术。它在密度域中运用相当成功。
一幅图像f(x,y)可以看成由两个分量组合而成,即
f(x,y)=i(x,y).r(x,y)
i(x,y)为照明分量(入射分量),是入射到景物上的光强度;
r(x,y)为反射分量,是受到景物反射的光强度。
具体步骤如下:
(1)先对上式的两边同时取对数,即
Inf(x,y)=Ini(x,y)+Inr(x,y)
(2)将上式两边取傅立叶变换,得
F(u,v)=I(u,v)+R(u,v)
(3)用一个频域函数H(u,v)处理F(u,v),可得到
H(u,v)F(u,v)=H(u,v)I(u,v)+H(u,v)R(u,v)
(4)逆傅立叶变换到空间域得
Hff(x,y)=hi(x,y)+hr(x,y)
可见增强后得图像是由对应照度分量与反射分量得两部分叠加而成。
(5)再将上式两边取指数,得
g(x,y)=exp|hff(x,y)|=exp|hi(x,y)|exp|hr(x,y)|
这里,称作同态滤波函数,它可以分别作用于照度分量和反射分量上。
一幅图像得照明分量通常用慢变化来表征,而反射分量则倾向于急剧变换。所以图像取对数后得傅立叶变换的低频部分主要对应照度分量,而高频部分主要对应反射分量。适当的选择滤波器函数将会对傅立叶变换中的低频部分和高频部分产生不同的响应。处理结果会使像元灰度的动态范围或图像对比度得到增强。
</div>