#include <iostream>
#include <vector>
using namespace std;


int main() /* 矩阵A的QR分解*/
{


    // 动态分配内存
    int m = 3; // 行数
    int n = 3; // 列数


    // 初始化矩阵A
    double A[3][3] = {
        {1, 2, 2},
        {2, 1, 2},
        {1, 2, 1}
    };

    double R[3][3] = { 0 };
    double Q[3][3] = { 0 };



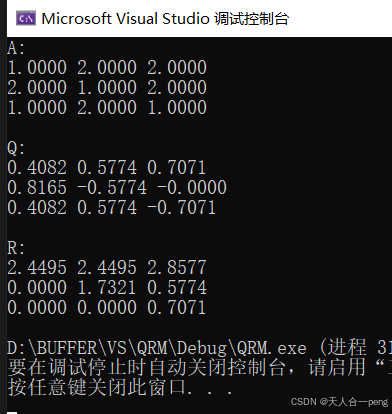
    cout << "A:" << endl; //输出矩阵A
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            printf("%.4f ", A[i][j]);
        }
        cout << endl;
    }

    for (int k = 0; k < n; k++)
    {
        double MOD = 0;
        for (int i = 0; i < n; i++)
        {
            MOD += A[i][k] * A[i][k];
        }
        R[k][k] = sqrt(MOD); // 计算A第k列的模长，由公式(4)等于R的对角线元素||A:k||
        for (int i = 0; i < n; i++)
        {
            Q[i][k] = A[i][k] / R[k][k]; // 由公式(2)，A第k列标准化之后成为Q的第k列
        }

        for (int i = k + 1; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                R[k][i] += A[j][i] * Q[j][k]; // 由公式(4)，计算R的上三角部分
            }
            for (int j = 0; j < n; j++)
            {
                A[j][i] -= R[k][i] * Q[j][k]; // 由公式(1)，计算更新A的每一列
            }
        }
    }

    cout << endl;
    cout << "Q:" << endl; //输出矩阵Q
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            printf("%.4f ", Q[i][j]);
        }
        cout << endl;
    }

    cout << endl;
    cout << "R:" << endl; //输出矩阵R
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            printf("%.4f ", R[i][j]);
        }
        cout << endl;
    }

    return 0;
}




//动态分配内存

//int main3() /* 矩阵A的QR分解*/
//{
//
//
//    // 动态分配内存
//    int m = 3; // 行数
//    int n = 3; // 列数
//    double** A = (double**)malloc(m * sizeof(double*));
//    double** Q = (double**)malloc(m * sizeof(double*));
//    double** R = (double**)malloc(n * sizeof(double*));
//
//    for (int i = 0; i < m; i++) {
//        A[i] = (double*)malloc(n * sizeof(double));
//        Q[i] = (double*)malloc(n * sizeof(double));
//        R[i] = (double*)malloc(n * sizeof(double));
//    }
//
//    // 初始化矩阵A
//    double A_values[3][3] = {
//        {1, 2, 2},
//        {2, 1, 2},
//        {1, 2, 1}
//    };
//
//    for (int i = 0; i < m; i++) {
//        for (int j = 0; j < n; j++) {
//            A[i][j] = A_values[i][j];
//        }
//    }
//
//
//    // 初始化矩阵A
//    double A[3][3] = {
//        {1, 2, 2},
//        {2, 1, 2},
//        {1, 2, 1}
//    };
//
//    double R[3][3] = { 0 };
//    double Q[3][3] = { 0 };
//
//
//
//    cout << "A:" << endl; //输出矩阵A
//    for (int i = 0; i < n; i++)
//    {
//        for (int j = 0; j < n; j++)
//        {
//            printf("%.4f ", A[i][j]);
//        }
//        cout << endl;
//    }
//
//    for (int k = 0; k < n; k++)
//    {
//        double MOD = 0;
//        for (int i = 0; i < n; i++)
//        {
//            MOD += A[i][k] * A[i][k];
//        }
//        R[k][k] = sqrt(MOD); // 计算A第k列的模长，由公式(4)等于R的对角线元素||A:k||
//        for (int i = 0; i < n; i++)
//        {
//            Q[i][k] = A[i][k] / R[k][k]; // 由公式(2)，A第k列标准化之后成为Q的第k列
//        }
//
//        for (int i = k + 1; i < n; i++)
//        {
//            for (int j = 0; j < n; j++)
//            {
//                R[k][i] += A[j][i] * Q[j][k]; // 由公式(4)，计算R的上三角部分
//            }
//            for (int j = 0; j < n; j++)
//            {
//                A[j][i] -= R[k][i] * Q[j][k]; // 由公式(1)，计算更新A的每一列
//            }
//        }
//    }
//
//    cout << endl;
//    cout << "Q:" << endl; //输出矩阵Q
//    for (int i = 0; i < n; i++)
//    {
//        for (int j = 0; j < n; j++)
//        {
//            printf("%.4f ", Q[i][j]);
//        }
//        cout << endl;
//    }
//
//    cout << endl;
//    cout << "R:" << endl; //输出矩阵R
//    for (int i = 0; i < n; i++)
//    {
//        for (int j = 0; j < n; j++)
//        {
//            printf("%.4f ", R[i][j]);
//        }
//        cout << endl;
//    }
//
//    // 释放内存
//    for (int i = 0; i < m; i++) {
//        free(A[i]);
//        free(Q[i]);
//    }
//    for (int i = 0; i < n; i++) {
//        free(R[i]);
//    }
//    free(A);
//    free(Q);
//    free(R);
//
//    return 0;
//}





//
//int main1() /* 矩阵A的QR分解*/
//{
//    vector<vector<double>> a = { {1,2,2},{2,1,2},{1,2,1} };
//    int n = a.size();
//    vector<vector<double>> q(n, vector<double>(n));
//    vector<vector<double>> r(n, vector<double>(n));
//
//
//
//    cout << "A:" << endl; //输出矩阵A
//    for (int i = 0; i < n; i++)
//    {
//        for (int j = 0; j < n; j++)
//        {
//            printf("%.4f ", a[i][j]);
//        }
//        cout << endl;
//    }
//
//    for (int k = 0; k < n; k++)
//    {
//        double MOD = 0;
//        for (int i = 0; i < n; i++)
//        {
//            MOD += a[i][k] * a[i][k];
//        }
//        r[k][k] = sqrt(MOD); // 计算A第k列的模长，由公式(4)等于R的对角线元素||A:k||
//        for (int i = 0; i < n; i++)
//        {
//            q[i][k] = a[i][k] / r[k][k]; // 由公式(2)，A第k列标准化之后成为Q的第k列
//        }
//
//        for (int i = k + 1; i < n; i++)
//        {
//            for (int j = 0; j < n; j++)
//            {
//                r[k][i] += a[j][i] * q[j][k]; // 由公式(4)，计算R的上三角部分
//            }
//            for (int j = 0; j < n; j++)
//            {
//                a[j][i] -= r[k][i] * q[j][k]; // 由公式(1)，计算更新A的每一列
//            }
//        }
//    }
//
//    cout << endl;
//    cout << "Q:" << endl; //输出矩阵Q
//    for (int i = 0; i < n; i++)
//    {
//        for (int j = 0; j < n; j++)
//        {
//            printf("%.4f ", q[i][j]);
//        }
//        cout << endl;
//    }
//
//    cout << endl;
//    cout << "R:" << endl; //输出矩阵R
//    for (int i = 0; i < n; i++)
//    {
//        for (int j = 0; j < n; j++)
//        {
//            printf("%.4f ", r[i][j]);
//        }
//        cout << endl;
//    }
//
//    return 0;
//}
//

Matlab