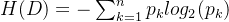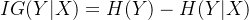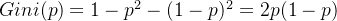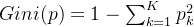决策树-分类

概念：

1、决策节点通过条件判断而进行分支选择的节点。如：将某个样本中的属性值(特征值)与决策节点上的值进行比较，从而判断它的流向。

2、叶子节点没有子节点的节点，表示最终的决策结果。

3、决策树的深度所有节点的最大层次数。

决策树具有一定的层次结构，根节点的层次数定为0，从下面开始每一层子节点层次数增加

优点

可解释性强：决策树的结构直观易懂，它通过树形结构展示了从输入特征到输出结果的决策过程，每个节点的条件判断和分支走向都清晰明了，人们可以很容易地理解模型是基于哪些特征和规则进行决策的，这使得决策树在需要解释决策依据的场景中，如医疗诊断、金融风险评估等领域，具有很大的优势。
数据处理能力强：决策树对数据类型的适应性很强，能够同时处理数值型和类别型数据，不需要对数据进行复杂的预处理或转换。而且它可以处理具有缺失值的数据，在构建树的过程中，能够自动处理缺失值的情况，不会因为部分数据缺失而导致模型无法训练或预测。
计算复杂度低：在训练和预测阶段，决策树的计算复杂度相对较低，尤其是对于小规模数据集，训练速度快，能够快速生成模型并进行预测。这使得决策树在一些对实时性要求较高的场景中，如在线广告投放、实时路况预测等，能够快速给出结果。
模型构建灵活：决策树可以根据数据的特点自动学习和生成不同的树形结构，能够捕捉到数据中的复杂关系和非线性特征，不需要事先假设数据的分布或关系形式。同时，通过调整树的深度、节点分裂条件等参数，可以很容易地控制模型的复杂度，以适应不同的数据集和任务需求。
可进行特征选择：在构建决策树的过程中，通过计算每个特征的信息增益、基尼指数等指标，可以评估各个特征对分类或回归任务的重要性，从而自动选择对目标变量最有影响力的特征，实现特征选择的功能，有助于减少数据维度，提高模型的效率和准确性。

缺点

容易过拟合：决策树在训练过程中可能会过度拟合训练数据，即模型过于复杂，学习到了训练数据中的噪声和细节，而这些噪声和细节并不能代表数据的真实分布规律，导致在测试集或新数据上的泛化能力较差，预测准确率下降。
稳定性差：决策树的结构和性能对训练数据的微小变化比较敏感，例如数据集中增加或删除少量样本，或者特征的取值发生一些小的变化，都可能导致决策树的结构发生较大的改变，从而影响模型的稳定性和可靠性，使得不同训练集得到的决策树模型差异较大，难以保证模型的一致性和准确性。
缺乏全局最优性：决策树的构建是一个贪心算法的过程，它在每个节点上只考虑当前的局部最优解，而不考虑整体的最优情况，这可能导致最终生成的决策树不是全局最优的，即可能存在其他树形结构能够更好地拟合数据或具有更好的泛化性能，但由于贪心算法的局限性，无法找到这些更优的结构。
不适合处理高维数据：当数据的维度很高，即特征数量很多时，决策树的性能可能会受到影响，随着特征数量的增加，决策树可能会变得非常复杂，分支过多，导致训练时间过长，模型难以理解和解释，而且容易出现过拟合现象。
对数据分布敏感：决策树在处理数据分布不均衡的问题时表现较差，如果训练数据中某个类别的样本数量远远多于其他类别，决策树可能会倾向于将大多数样本划分到数量较多的类别中，导致对少数类别的分类效果不佳，模型对不同类别的预测准确率存在较大差异

1. 基于信息增益决策树的建立

(1) 信息熵

信息熵描述的是不确定性。信息熵越大，不确定性越大。信息熵的值越小，则D的纯度越高。

假设样本集合D共有N类，第k类样本所占比例为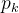 p_k ，则D的信息熵为： $H(D) = -\sum_{k=1}^{n}p_klog_2(p_k)$

(2) 信息增益

信息增益是一个统计量，用来描述一个属性区分数据样本的能力。信息增益越大，那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量, 信息增益公式：

IG(Y|X) = H(Y) - H(Y|X)

2. 基于基尼指数决策树的建立(了解)

基尼指数（Gini Index）是决策树算法中用于评估数据集纯度的一种度量，基尼指数衡量的是数据集的不纯度，或者说分类的不确定性。在构建决策树时，基尼指数被用来决定如何对数据集进行最优划分，以减少不纯度。

基尼指数的计算

对于一个二分类问题，如果一个节点包含的样本属于正类的概率是 (p)，则属于负类的概率是 (1-p)。那么，这个节点的基尼指数 (Gini(p)) 定义为：
Gini(p) = 1 - p^2 - (1-p)^2 = 2p(1-p)

对于多分类问题，如果一个节点包含的样本属于第 k 类的概率是 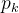p_k ，则节点的基尼指数定义为：

$Gini(p) = 1 - \sum_{k=1}^{K} p_k^2$

基尼指数的意义

当一个节点的所有样本都属于同一类别时，基尼指数为 0，表示纯度最高。
当一个节点的样本均匀分布在所有类别时，基尼指数最大，表示纯度最低。

决策树中的应用

在构建决策树时，我们希望每个内部节点的子节点能更纯，即基尼指数更小。因此，选择分割特征和分割点的目标是使子节点的平均基尼指数最小化。具体来说，对于一个特征，我们计算其所有可能的分割点对应的子节点的加权平均基尼指数，然后选择最小化这个值的分割点。这个过程会在所有特征中重复，直到找到最佳的分割特征和分割点。

例如，考虑一个数据集 (D)，其中包含 (N) 个样本，特征 (A) 将数据集分割为 $|D_1|$和 $|D_2|$ ，则特征 (A) 的基尼指数为：
$Gini_A = \frac{|D_1|}{|D|} Gini(D_1) + \frac{|D_2|}{|D|} Gini(D_2)$

其中 |D_1| 和 |D_2| 分别是子集 D_1 和 D_2 中的样本数量。

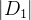
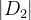
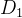
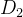
通过这样的方式，决策树算法逐步构建一棵树，每一层的节点都尽可能地减少基尼指数，最终达到对数据集的有效分类。

class sklearn.tree.DecisionTreeClassifier(....)
参数：
criterion "gini" "entropy” 默认为="gini" 
	当criterion取值为"gini"时采用 基尼不纯度（Gini impurity）算法构造决策树，
	当criterion取值为"entropy”时采用信息增益（ information gain）算法构造决策树.
max_depth	int, 默认为=None  树的最大深度

# 可视化决策树
function sklearn.tree.export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
参数：
	estimator决策树预估器
	out_file生成的文档
    feature_names节点特征属性名
功能:
    把生成的文档打开，复制出内容粘贴到"http://webgraphviz.com/"中，点击"generate Graph"会生成一个树型的决策树图

示例：坦尼克号乘客生存

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier, export_graphviz
# 1、获取数据
titanic = pd.read_csv("src/titanic/titanic.csv")
titanic.head()
# 筛选特征值和目标值
x = titanic[["pclass", "age", "sex"]]
y = titanic["survived"]

#2、数据处理
# 1）缺失值处理， 因为其中age有缺失值。
x["age"].fillna(x["age"].mean(), inplace=True)

# 2) 转换成字典， 因为其中数据必须为数字才能进行决策树，所在先转成字典，后面又字典特征抽取，这样之后的数据就会是数字了, 鸢尾花的数据本来就全部是数字，所以不需要这一步。
"""
x.to_dict(orient="records") 这个方法通常用于 Pandas DataFrame 对象，用来将 DataFrame 转换为一个列表，其中列表的每一个元素是一个字典，对应于 DataFrame 中的一行记录。字典的键是 DataFrame 的列名，值则是该行中对应的列值。
假设你有一个如下所示的 DataFrame x:
   A  B  C
0  1  4  7
1  2  5  8
2  3  6  9
执行 x.to_dict(orient="records")，你会得到这样的输出：
[
    {'A': 1, 'B': 4, 'C': 7},
    {'A': 2, 'B': 5, 'C': 8},
    {'A': 3, 'B': 6, 'C': 9}
]
"""
x = x.to_dict(orient="records")
# 3)、数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 4)、字典特征抽取
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train) #稀疏矩阵
x_test = transfer.transform(x_test)

# 3）决策树预估器
estimator = DecisionTreeClassifier(criterion="entropy", max_depth=8)
estimator.fit(x_train, y_train)

# 4）模型评估
# 方法1：直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)

# 方法2：计算准确率
score = estimator.score(x_test, y_test)
print("准确率为：\n", score)


# 6）预测
x_test = transfer.transform([{'pclass': '1rd', 'age': 22.0, 'sex': 'female'}])
index=estimator.predict(x_test)
print("预测1:\n",index)#[1]  头等舱的就可以活下来
x_test = transfer.transform([{'pclass': '3rd', 'age': 22.0, 'sex': 'female'}])
index=estimator.predict(x_test)
print("预测2:\n",index)#[0]  3等舱的活不下来

# 可视化决策树
export_graphviz(estimator, out_file="titanic_tree.dot", feature_names=transfer.get_feature_names_out())