CavalierContours 二维线操作
2D polyline library for offsetting, combining, etc.
用于偏移、交并补等组合等操作的 2D 多折段线库。
Polyline Structure 多段线结构
Polylines are defined by a sequence of vertexes and a bool indicating whether the polyline is closed or open. Each vertex has a 2D position (x and y) as well as a bulge value. Bulge is used to define arcs, where bulge = tan(theta/4). theta is the arc sweep angle from the starting vertex position to the next vertex position. If the polyline is closed then the last vertex connects to the first vertex, otherwise it does not (and the last vertex bulge value is unused). See for more details regarding bulge calculations.
多段折线由一系列顶点和一个布尔值定义,该布尔值指示折线是闭合的还是开放的。每个顶点都有一个 2D 位置(x 和 y)以及一个凸起值。凸起用于定义弧,其中凸起 = tan(theta/4)。θ 是从起始顶点位置到下一个顶点位置的弧扫描角。如果折线闭合,则最后一个顶点连接到第一个顶点,否则不连接(并且最后一个顶点凸起值未使用)。
示例
#include "cavc/polylineoffset.hpp"
// input polyline
cavc::Polyline<double> input;
// add vertexes as (x, y, bulge)
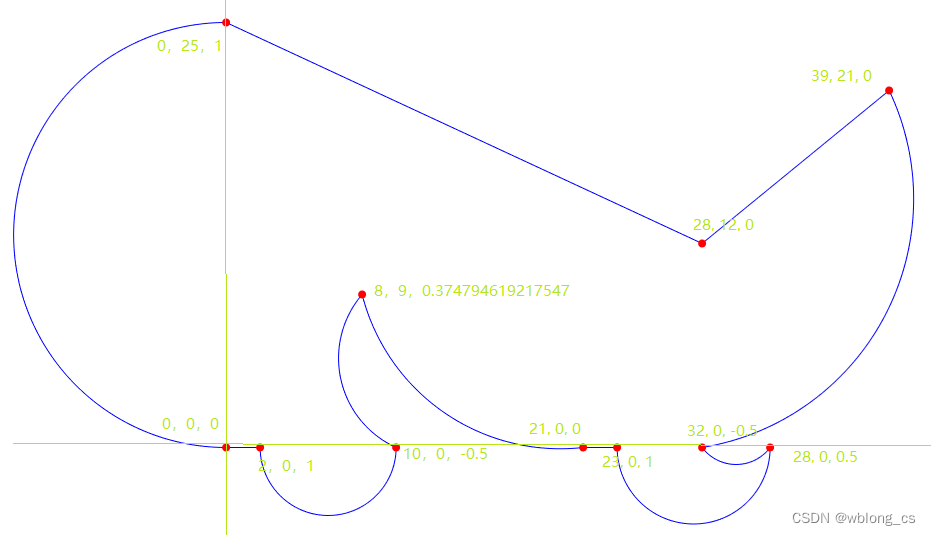
input.addVertex(0, 25, 1);
input.addVertex(0, 0, 0);
input.addVertex(2, 0, 1);
input.addVertex(10, 0, -0.5);
input.addVertex(8, 9, 0.374794619217547);
input.addVertex(21, 0, 0);
input.addVertex(23, 0, 1);
input.addVertex(32, 0, -0.5);
input.addVertex(28, 0, 0.5);
input.addVertex(39, 21, 0);
input.addVertex(28, 12, 0);
input.isClosed() = true;
// compute the resulting offset polylines, offset = 3
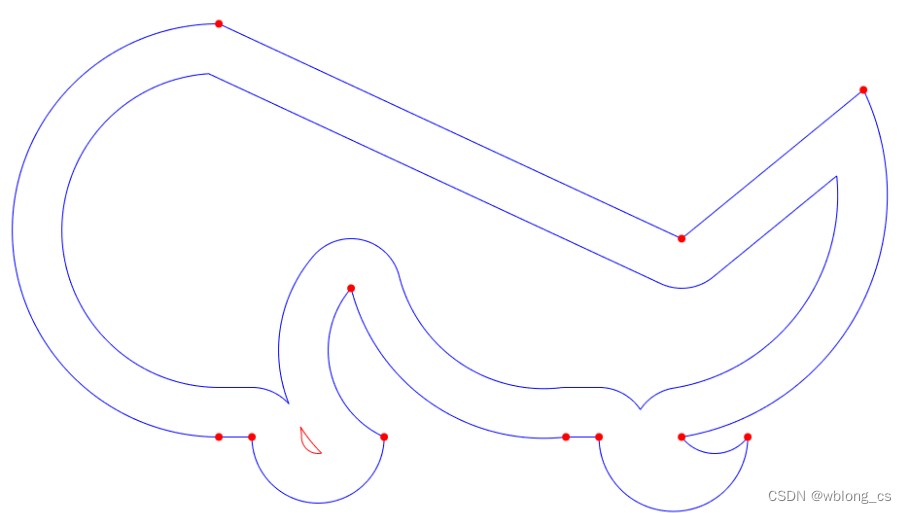
std::vector<cavc::Polyline<double>> results = cavc::parallelOffset(input, 3.0);
输入多线段(包含弧段)
结果:
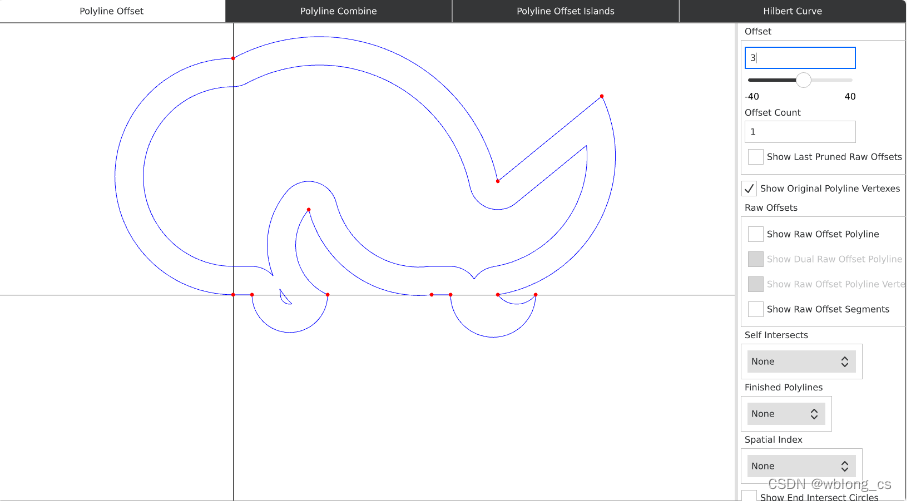
Demo
//
git clone https://github.com/jbuckmccready/CavalierContours.git
//
vcpkg install gtest:x64-windows
// 试用vcpkg安装Qt环境和相关库
vcpkg install qt5[core,quickcontrols2]:x64-windows
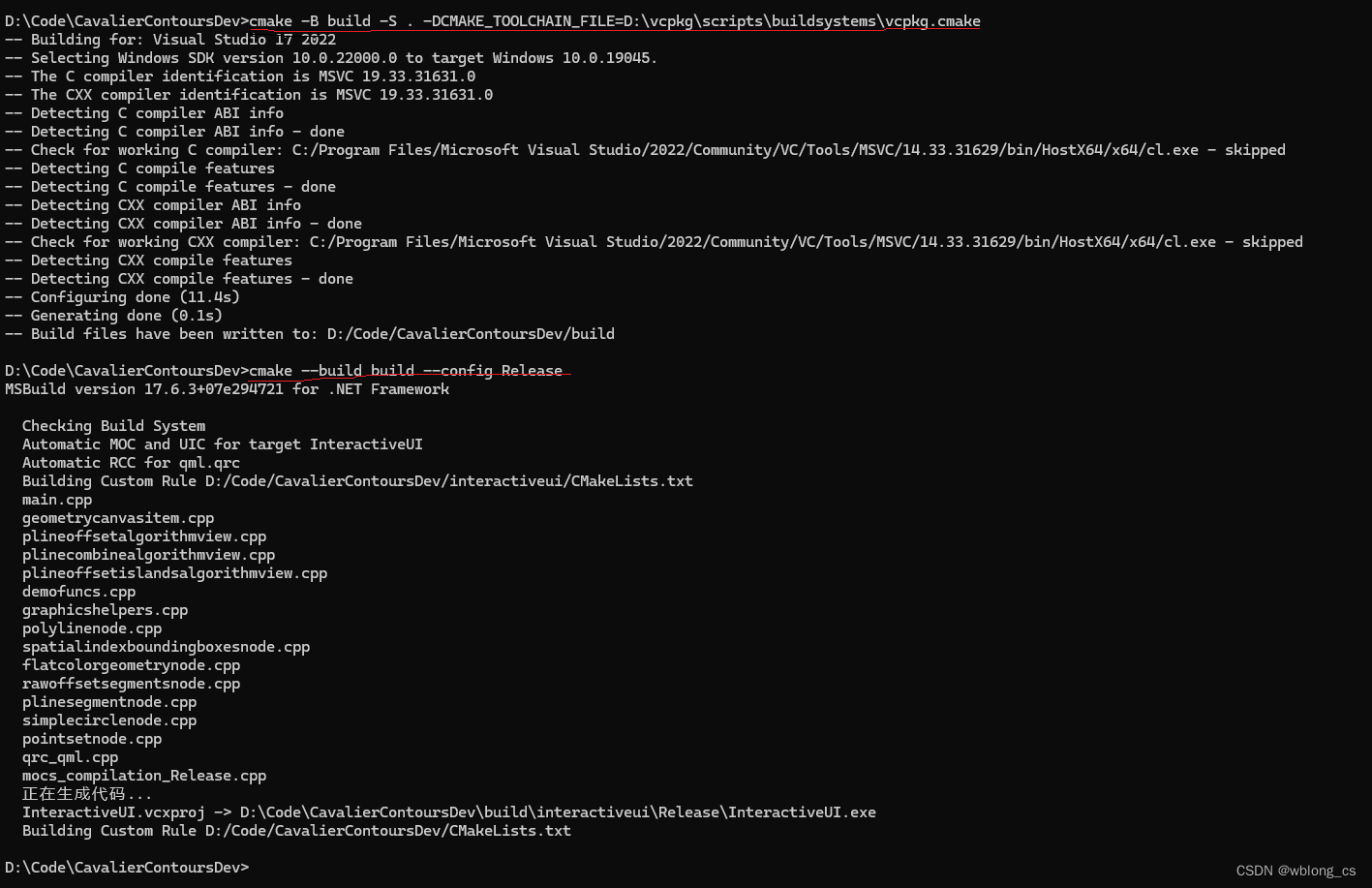
cmake -B build -S . -DCMAKE_TOOLCHAIN_FILE=D:\vcpkg\scripts\buildsystems\vcpkg.cmake
cmake --build build --config Release
Polyline Offset
Polyline Combine 交并补
Polyline Offset Islands
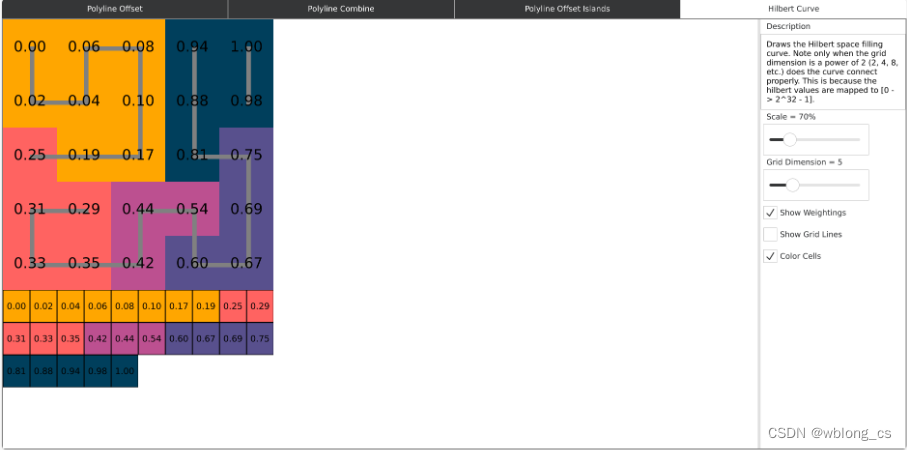
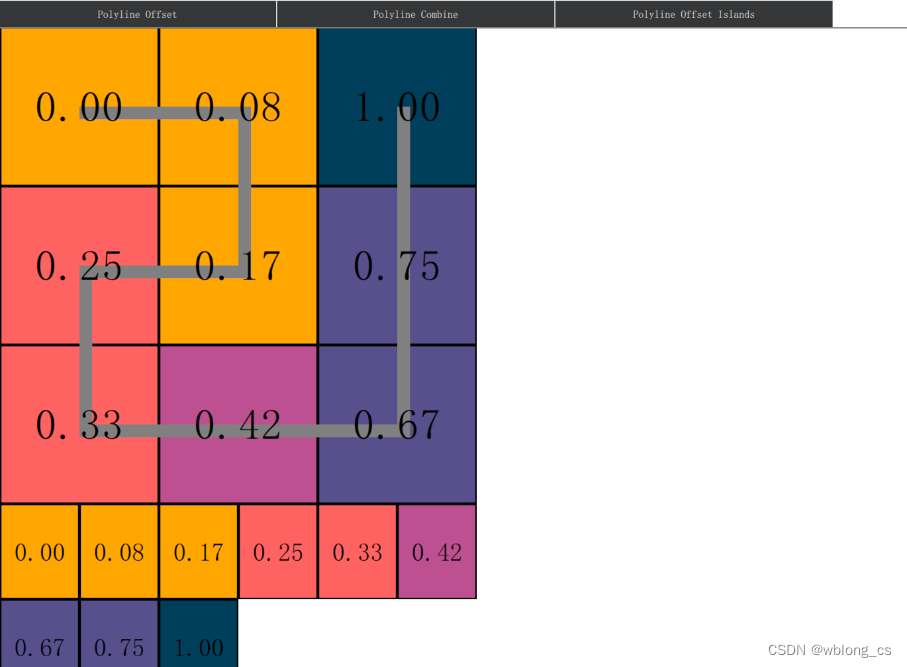
Hilbert Curve 希尔伯特曲线
Algorithm Complexity and 2D Spatial Indexing算法复杂度和二维空间索引
该算法需要查找自相交,测试点与原始折线之间的距离,测试新线段与原始折线之间的相交,以及将开放的折线首尾相连。这些步骤的幼稚方法通常会导致 O(n2) 算法复杂性,其中每个段必须针对其他每个段进行测试,并且必须针对每个段测试每个点。
该库使用的方法是使用打包的 Hilbert R-Tree [4]空间索引。有关 c++ 实现,请参阅 staticspatialindex.hpp。这导致典型输入的算法复杂度为 O(n log n),病理输入的算法复杂度为 O(n2)。
Packed Hilbert R-Tree 希尔伯特 R-Tree
Here is an image of a closed polyline approximating a circle using 100 line segments (blue lines and red vertexes) with spatial index bounding boxes made visible (magenta, orange, and light green boxes). The root of the R-Tree is the light green box, its children are the orange boxes, and its grand children are the magenta boxes.
这是使用 100 个线段(蓝线和红色顶点)近似圆的闭合折线图像,空间索引边界框(洋红色、橙色和浅绿色框)可见。R-Tree 的根是浅绿色的盒子,它的子是橙色的盒子,它的孙子是洋红色的盒子。
UE 集成
直接以源码的形式集成。
参考
1、https://github.com/jbuckmccready/CavalierContours.git
2、https://jbuckmccready.github.io/CavalierContoursWebDemo/
3、https://www.lee-mac.com/bulgeconversion.html
4、https://en.wikipedia.org/wiki/Hilbert_R-tree#Packed_Hilbert_R-trees
5、https://github.com/jbuckmccready/CavalierContoursDev.git
6、https://blog.csdn.net/mrbaolong/article/details/121887605【空间填充曲线】
7、https://blog.csdn.net/mrbaolong/article/details/120854261【RTree 空间索引】