人工智能和机器学习之线性代数（一）

本文Linear Algebra 101 for AI/ML – Part 1将介绍向量和矩阵的基础知识以及开源的机器学习框架PyTorch。

基本定义

标量（Scalar）

标量是表示无方向的单个数值，仅仅表示程度或大小。在编程术语中，可以将标量视为包含单个数字的简单变量，例如整数或浮点数。标量的示例包括 温度（temperature）、年龄（age） 和 体重（weight）。

向量（Vector）

向量是标量的有序列表。之所以向量是有序的，因为标量在向量中的位置很重要。如下图所示 向量y表示电影《复仇者联盟：终局之战》Avengers: Endgame，向量中的每一个数字描述了影片的一个特定属性，其中action表示该电影属于动作类题材的占比为0.99，comedy表示属于喜剧题材的占比为0.52，drama表示属于戏剧题材的占比为0.45，horror表示属于恐怖题材的占比为0.10，romance表示属于浪漫题材的占比为0.26。

这部电影的动作值为 0.99，恐怖值为 0.10。这表明这部电影更像是一部动作片，而不是一部恐怖片。

如果将 action 的值与 horor 的值交换，则该向量将不再准确表示电影《复仇者联盟：终局之战》，它不是恐怖电影。这就是顺序很重要的原因，即，改变顺序后变成另外一个向量。

向量总是以列或行的形式排列。以下是不同长度的行或列形式的向量。

注意，向量要么有一行，要么有一列。如果想要一个具有多行和多列的数学对象，该怎么办？这就是矩阵发挥作用的地方。

矩阵（Matrix）

如果标量是单个数字，向量是标量的一维有序列表，则矩阵是标量的二维数组。下面X 是一个示例矩阵（4行2列）。

每行对应于一个家庭的地址，即表示一个家庭。第一列表示家中卧室的数量，第二列表示浴室的数量。故矩阵X表示了多个家庭，以及每个家庭的特有属性。

二维矩阵也可以表示为向量的形式：

$$X=\left[\begin{array}{c}\vec{a}\\ \vec{b}\\ \vec{c}\\ \vec{d}\end{array}\right]$$

向量a表示地址为123 Maple Grove Lane的家庭：
$$\vec{a}=\left[\begin{array}{c}3\\ 3\end{array}\right]$$
向量b表示地址为888 Ocean View Terrace的家庭：
$$\vec{b}=\left[\begin{array}{c}4\\ 3\end{array}\right]$$
向量c表示地址为100 Birch Street的家庭：
$$\vec{c}=\left[\begin{array}{c}5\\ 3\end{array}\right]$$
向量d表示地址为987 Sunflower Court的家庭：
$$\vec{d}=\left[\begin{array}{c}5\\ 4\end{array}\right]$$

数学符号表示

实数集合R是数学家对在日常生活中使用的所有数字的表示方式：实数数轴线上的所有整数(whole numbers)、负数(negative numbers,)、分数(fractions)、小数（decimal numbers）和无理数( irrational numbers)。

下面的x表示任意一个实数标量：

$$x\in R$$

下面的表示任意一个m维的向量：
$$\left[\begin{array}{c}{x}_0\\ x_1\\ ⋮\\ x_{m-1}\end{array}\right]\in R^m$$
下面表示任意m x n的矩阵：
$$\left[\begin{array}{cccc}{x}_{0,0}& x_{0,1}& \dots & x_{0,n-1}\\ x_{1,0}& x_{1,1}& \dots & x_{1,n-1}\\ ⋮& ⋮& ⋮& ⋮\\ x_{m-1,0}& x_{m-1,1}& \dots & x_{m-1,n-1}\end{array}\right]\in R^{m\times n}$$

使用 PyTorch 进行操作

上面章节已经建立了向量和矩阵的定义及其数学符号，本节将在代码中简单尝试一下，加深一下印象。为此，将使用 PyTorch开源机器学习框架。PyTorch 在整个学术界和工业界广泛用于 OpenAI、Amazon、Meta、Salesforce、斯坦福大学等机构和公司的尖端 AI 研究和生产级软件，以及数千家初创公司，因此积累该框架的经验将是实用的。请访问官方 PyTorch 安装说明页面以开始使用。

张量（Tensors）

向量具有1 维，矩阵具有2 个维度，那么涵盖 3 个或更多维度的通用术语是什么？答案：张量。实际上，向量和矩阵也是张量，因为张量是任何N 维数字数组。张量是 PyTorch 中的基本单位。使用 PyTorch 函数 torch.tensor（...） 创建向量和矩阵。

import torch
>>> a = torch.rand((3, 4, 2)) # Create a three
tensor([[[0.8856, 0.9232],    # dimensional tensor
         [0.0250, 0.2977],    # with random values
         [0.4745, 0.2243],
         [0.3107, 0.9159]],

        [[0.3654, 0.3746],
         [0.4026, 0.4557],
         [0.9426, 0.0865],
         [0.3805, 0.5034]],

        [[0.3843, 0.9903],
         [0.6279, 0.2222],
         [0.0693, 0.0140],
         [0.6222, 0.3590]]])
>>> a.shape
torch.Size([3, 4, 2]) # the tensor's dimensions

定义变量

定义向量a和矩阵m：

import torch
a = torch.tensor([[3], [4], [5], [5]])
m = torch.tensor([[3,4], [5,6]])

$$a=\left[\begin{array}{c}3\\ 4\\ 5\\ 5\end{array}\right]\in R^{4\times 1}$$

$$m=\left[\begin{array}{cc}3& 4\\ 5& 6\end{array}\right]$$

四则运算

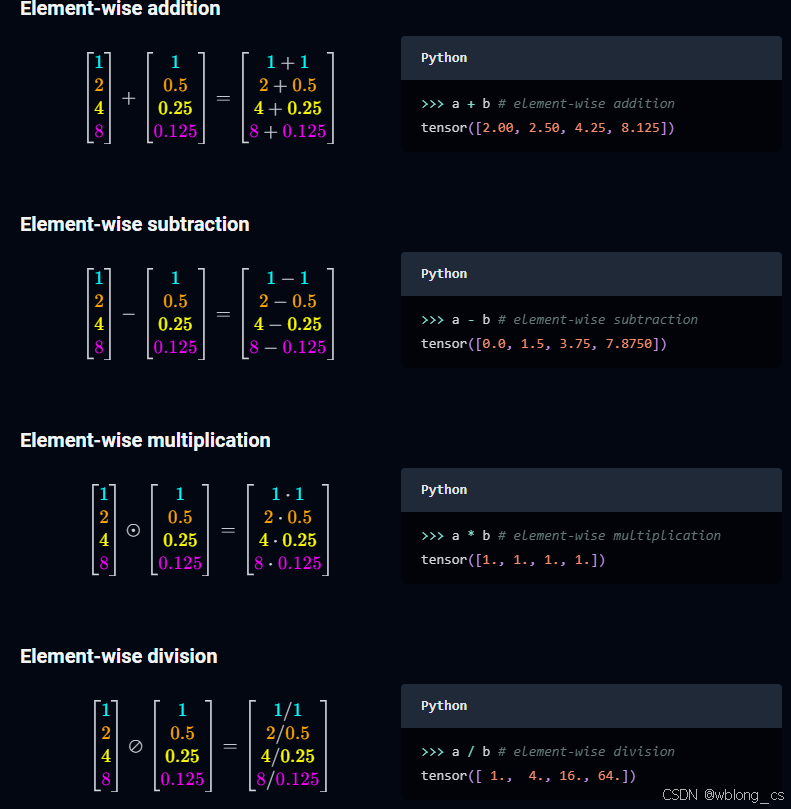
简单的加减乘除四则运算

>>> import torch
>>> a = torch.tensor([1.0, 2.0, 4.0, 8.0])
>>> b = torch.tensor([1.0, 0.5, 0.25, 0.125])
>>> a + b # element-wise addition
tensor([2.00, 2.50, 4.25, 8.125])
>>> a - b # element-wise subtraction
tensor([0.0, 1.5, 3.75, 7.8750])
>>> a * b # element-wise multiplication
tensor([1., 1., 1., 1.])
>>> a / b # element-wise division
tensor([ 1.,  4., 16., 64.])

Sigmoid运算

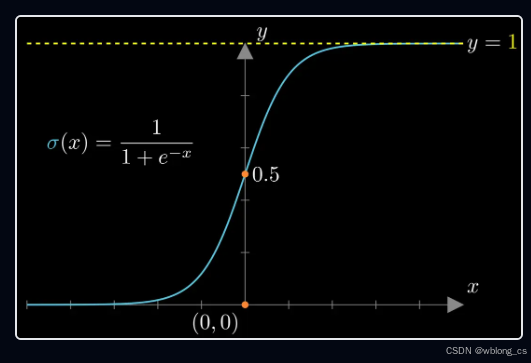
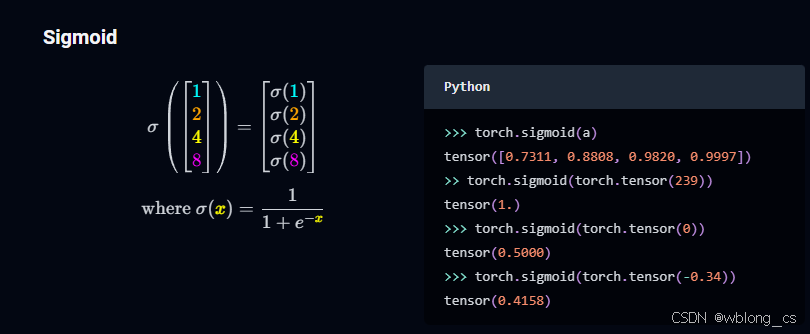
sigmoid(x) 函数将x压缩到范围（0,1）, 请注意，只有具有任意较大的值并且希望将它们压缩为介于 0 和 1 之间的值范围时，这非常有用。有时将 sigmoid 的输出解释为概率很有用。

$$\sigma \left(x\right)=\frac{1}{1+e^{-x}}$$

>>> torch.sigmoid(a)
tensor([0.7311, 0.8808, 0.9820, 0.9997])
>> torch.sigmoid(torch.tensor(239))
tensor(1.)
>>> torch.sigmoid(torch.tensor(0))
tensor(0.5000)
>>> torch.sigmoid(torch.tensor(-0.34))
tensor(0.4158)

ReLU运算

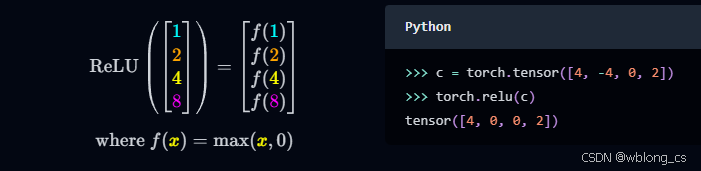
ReLU 函数充当过滤器。任何正输入都保持不变，但任何负输入都变为零。

>>> c = torch.tensor([4, -4, 0, 2])
>>> torch.relu(c)
tensor([4, 0, 0, 2])