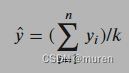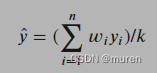昇思MindSpore学习笔记3-02热门LLM及其他AI应用--K近邻算法实现红酒聚类

摘要：

介绍了K近邻算法，记录了MindSporeAI框架使用部分wine数据集进行KNN实验的步聚和方法。包括环境准备、下载红酒数据集、加载数据和预处理、搭建模型、进行预测等。

一、KNN概念

1. K近邻算法K-Nearest-Neighbor(KNN)

用于分类和回归的非参数统计方法

Cover、Hart于1968年提出

机器学习最基础的算法之一。

确定样本类别

计算样本与所有训练样本的距离

找出最接近的k个样本

统计样本类别

投票

结果就是票数最多的类。

三个基本要素：

K值，样本分类由K个邻居的“多数表决”确定

K值太小容易产生噪声

K值太大类别界限模糊

距离度量，特征空间中两个样本间的相似度

距离越小越相似

Lp距离（p=2时，即为欧式距离）

曼哈顿距离

海明距离

分类决策规则

多数表决

基于距离加权的多数表决（权值与距离成反比）

2.预测算法（分类）的流程

（1）找出距离目标样本x_test最近的k个训练样本，保存至集合N中；

（2）统计集合N中各类样本个数 Ci,i=1,2,3,...,c；

（3）最终分类结果为Ci最大的那个类（argmaxCi）。

k取值重要。

根据问题和数据特点来确定。

带权重的k近邻算法

每个样本有不同的投票权重

3.回归预测

回归预测输出为所有邻居的标签均值：

yi为k个目标邻居样本的标签值

带样本权重的回归预测函数：

ωi为第个i样本的权重

4. 距离的定义

常用欧氏距离（欧几里得距离）

$R^{n}$ 空间中两点x和y之间的欧氏距离公式：

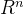
注意将特征向量的每个分量归一化

减少不同尺度的干扰

大数值特征分量会淹没小数值特征分量

其它距离

Mahalanobis距离

Bhattacharyya距离

二、环境配置

%%capture captured_output
# 实验环境已经预装了mindspore==2.2.14，如需更换mindspore版本，可更改下面mindspore的版本号
!pip uninstall mindspore -y
!pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspore==2.2.14
# 查看当前 mindspore 版本
!pip show mindspore

输出：

Name: mindspore
Version: 2.2.14
Summary: MindSpore is a new open source deep learning training/inference framework that could be used for mobile, edge and cloud scenarios.
Home-page: https://www.mindspore.cn
Author: The MindSpore Authors
Author-email: [email protected]
License: Apache 2.0
Location: /home/nginx/miniconda/envs/jupyter/lib/python3.9/site-packages
Requires: asttokens, astunparse, numpy, packaging, pillow, protobuf, psutil, scipy
Required-by: mindnlp

三、下载红酒数据集

1. Wine数据集

官网链接：UCI Machine Learning Repository

http://archive.ics.uci.edu/dataset/109/wine

数据内容：

意大利同一地区、三个不同品种葡萄酒化学分析结果。

包括每种葡萄酒中所含13种成分的量：

Alcohol	酒精
Malic acid	苹果酸
Ash	灰
Alcalinity of ash	灰的碱度
Magnesium	镁
Total phenols	总酚
Flavanoids	类黄酮
Nonflavanoid phenols	非黄酮酚
Proanthocyanins	原花青素
Color intensity	色彩强度
Hue	色调
OD280/OD315 of diluted wines	稀释酒的OD280/OD315
Proline	脯氨酸

方式一，从Wine数据集官网下载wine.data文件。

方式二，从华为云OBS中下载wine.data文件。

Key	Value	Key	Value
Data Set Characteristics	Multivariate	Number of Instances	178
Attribute Characteristics	Integer, Real	Number of Attributes	13
Associated Tasks	Classification	Missing Values?	No

2.下载数据集

from download import download

# 下载红酒数据集
url = "https://ascend-professional-construction-dataset.obs.cn-north-4.myhuaweicloud.com:443/MachineLearning/wine.zip"  
path = download(url, "./", kind="zip", replace=True)

输出：

Downloading data from https://ascend-professional-construction-dataset.obs.cn-north-4.myhuaweicloud.com:443/MachineLearning/wine.zip (4 kB)

file_sizes: 100%|██████████████████████████| 4.09k/4.09k [00:00<00:00, 2.35MB/s]
Extracting zip file...
Successfully downloaded / unzipped to ./

四、数据读取与处理

1.加载数据

导入os、numpy、MindSpore、matplotlib等模块

用context.set_context()配置运行模式、后端信息、硬件等

读取Wine数据集wine.data

查看部分数据。

%matplotlib inline
import os
import csv
import numpy as np
import matplotlib.pyplot as plt

import mindspore as ms
from mindspore import nn, ops

ms.set_context(device_target="CPU")

with open('wine.data') as csv_file:
    data = list(csv.reader(csv_file, delimiter=','))
print(data[56:62]+data[130:133])

输出：

[['1', '14.22', '1.7', '2.3', '16.3', '118', '3.2', '3', '.26', '2.03', '6.38', '.94', '3.31', '970'],
 ['1', '13.29', '1.97', '2.68', '16.8', '102', '3', '3.23', '.31', '1.66', '6', '1.07', '2.84', '1270'],
 ['1', '13.72', '1.43', '2.5', '16.7', '108', '3.4', '3.67', '.19', '2.04', '6.8', '.89', '2.87', '1285'],
 ['2', '12.37', '.94', '1.36', '10.6', '88', '1.98', '.57', '.28', '.42', '1.95', '1.05', '1.82', '520'],
 ['2', '12.33', '1.1', '2.28', '16', '101', '2.05', '1.09', '.63', '.41', '3.27', '1.25', '1.67', '680'],
 ['2', '12.64', '1.36', '2.02', '16.8', '100', '2.02', '1.41', '.53', '.62', '5.75', '.98', '1.59', '450'],
 ['3', '12.86', '1.35', '2.32', '18', '122', '1.51', '1.25', '.21', '.94', '4.1', '.76', '1.29', '630'],
 ['3', '12.88', '2.99', '2.4', '20', '104', '1.3', '1.22', '.24', '.83', '5.4', '.74', '1.42', '530'],
 ['3', '12.81', '2.31', '2.4', '24', '98', '1.15', '1.09', '.27', '.83', '5.7', '.66', '1.36', '560']]

三类样本（共178条）

自变量X为数据集的13个属性

因变量Y为数据集的3个类别

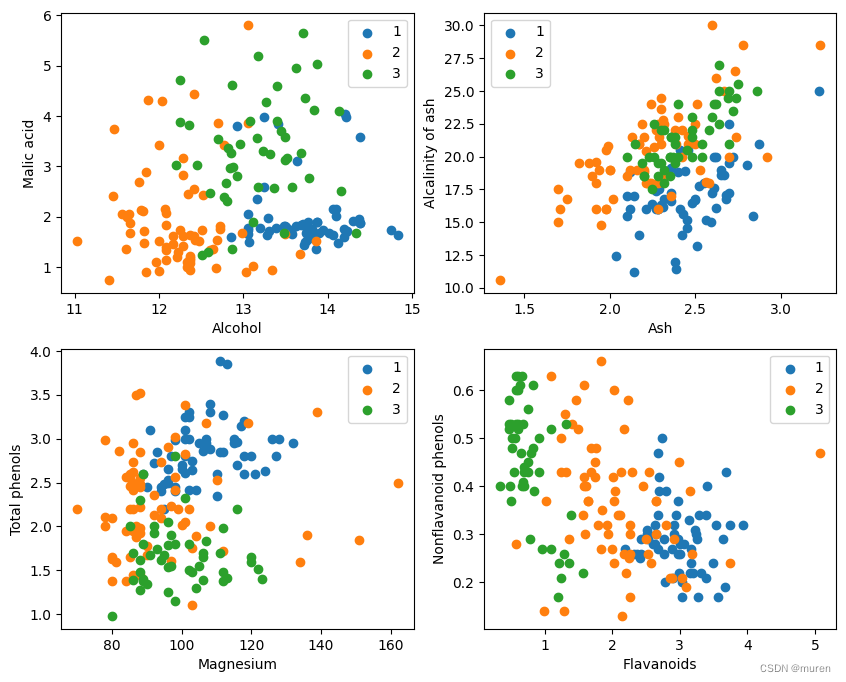
取样本的某两个属性进行2维可视化

可以看到在某两个属性上样本的分布情况以及可分性。

X = np.array([[float(x) for x in s[1:]] for s in data[:178]], np.float32)
Y = np.array([s[0] for s in data[:178]], np.int32)
attrs = ['Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols',
         'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue',
         'OD280/OD315 of diluted wines', 'Proline']
plt.figure(figsize=(10, 8))
for i in range(0, 4):
    plt.subplot(2, 2, i+1)
    a1, a2 = 2 * i, 2 * i + 1
    plt.scatter(X[:59, a1], X[:59, a2], label='1')
    plt.scatter(X[59:130, a1], X[59:130, a2], label='2')
    plt.scatter(X[130:, a1], X[130:, a2], label='3')
    plt.xlabel(attrs[a1])
    plt.ylabel(attrs[a2])
    plt.legend()
plt.show()

2.数据预处理

将数据集按128:50划分为训练集（已知类别样本）和验证集（待验证样本）：

train_idx = np.random.choice(178, 128, replace=False)
test_idx = np.array(list(set(range(178)) - set(train_idx)))
X_train, Y_train = X[train_idx], Y[train_idx]
X_test, Y_test = X[test_idx], Y[test_idx]

五、模型构建--计算距离

MindSpore算子

tile

square

ReduceSum

sqrt

TopK

矩阵运算并行计算

目标样本x和已分类训练样本X_train的距离

top k近邻

class KnnNet(nn.Cell):
    def __init__(self, k):
        super(KnnNet, self).__init__()
        self.k = k

    def construct(self, x, X_train):
        #平铺输入x以匹配X_train中的样本数
        x_tile = ops.tile(x, (128, 1))
        square_diff = ops.square(x_tile - X_train)
        square_dist = ops.sum(square_diff, 1)
        dist = ops.sqrt(square_dist)
        #-dist表示值越大，样本就越接近
        values, indices = ops.topk(-dist, self.k)
        return indices

def knn(knn_net, x, X_train, Y_train):
    x, X_train = ms.Tensor(x), ms.Tensor(X_train)
    indices = knn_net(x, X_train)
    topk_cls = [0]*len(indices.asnumpy())
    for idx in indices.asnumpy():
        topk_cls[Y_train[idx]] += 1
    cls = np.argmax(topk_cls)
    return cls

六、模型预测

验证KNN算法

k=5

验证精度接近80%

acc = 0
knn_net = KnnNet(5)
for x, y in zip(X_test, Y_test):
    pred = knn(knn_net, x, X_train, Y_train)
    acc += (pred == y)
    print('label: %d, prediction: %s' % (y, pred))
print('Validation accuracy is %f' % (acc/len(Y_test)))

输出：

label: 1, prediction: 1
label: 3, prediction: 3
label: 3, prediction: 3
label: 3, prediction: 3
label: 3, prediction: 3
label: 3, prediction: 3
label: 1, prediction: 1
label: 3, prediction: 1
label: 1, prediction: 1
label: 1, prediction: 2
label: 3, prediction: 3
label: 1, prediction: 1
label: 3, prediction: 3
label: 1, prediction: 1
label: 1, prediction: 1
label: 3, prediction: 2
label: 1, prediction: 1
label: 3, prediction: 3
label: 1, prediction: 1
label: 1, prediction: 3
label: 1, prediction: 1
label: 1, prediction: 1
label: 1, prediction: 3
label: 1, prediction: 1
label: 3, prediction: 2
label: 1, prediction: 1
label: 3, prediction: 2
label: 3, prediction: 2
label: 1, prediction: 1
label: 3, prediction: 1
label: 3, prediction: 1
label: 1, prediction: 1
label: 2, prediction: 3
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 3
label: 2, prediction: 2
label: 2, prediction: 3
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 3
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 2
label: 2, prediction: 2
Validation accuracy is 0.720000