pdf版本笔记的下载地址: MATLAB01_基本的数学运算与矩阵运算(访问密码:3834)
MATLAB01:基本的数学运算与矩阵运算
学习一门技术最好的方式就是阅读官方文档,可以查看MATLAB官方文档
MATLAB基本语法
变量
- MATLAB中的变量不需要声明.
- 使用
=为变量赋值
变量名
- 与大多数编程语言相同,MATLAB中的变量名是大小写敏感的.
- 变量名只能由[
0~9,a~z,A~z,_]组成,且变量名不能以数字开头.
保留变量不适合做变量名
MATLAB中有一些变量有其具体意义,不适合用作变量名.
| 变量 | 意义 |
|---|---|
ans | 上一句的运算的结果 |
i和j | 复数算子 |
Inf | 无穷 ∞ \infty ∞ |
eps | 浮点相对精度,即1.0到下一个浮点数之间的距离(值为2.2204e-16) |
NaN | 非数字 |
pi | 圆周率 π \pi π |
除此以外,使用iskeyword命令可以查看MATLAB语言所有的关键字,这些关键字也不允许被用作变量名.
变量名不应当覆盖内置函数名
在MATLAB中,变量的调用优先级(calling priority)高于函数,因此变量名不应该覆盖内置函数.
cos='This string.';
cos(8) % 对字符串进行索引取值,得到'r'
若某函数被变量名所覆盖,则调用clear <变量名>可以取消绑定在该函数名上的变量名
clear cos % 清除绑定在cos上的变量
cos(8) % 调用内置余弦函数运算得到-0.1455
clear是一个比较危险的命令,因为该命令后若不加参数,则表示清除当前工作区内的所有变量.
变量类型
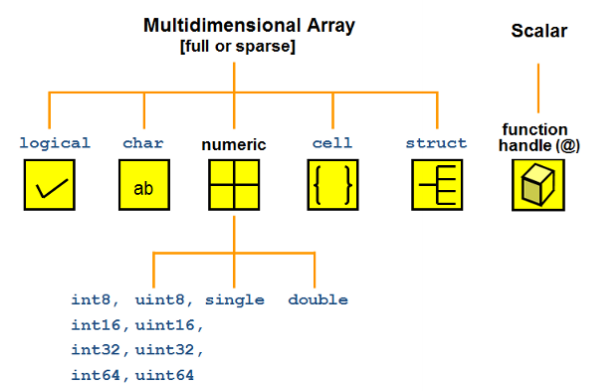
MATLAB中的变量类型有: logical,char,numeric,cell,struct以及由他们组成的数组或矩阵.
数字型变量的显示格式
我们直接定义的数字型变量,默认是以double形式存储的.
我们可以通过format <显示格式>改变数字型变量的显示格式.
| 显示格式 | 说明 | 例子 |
|---|---|---|
short | 短定点格式.显示小数点后4位 | 3.1416 |
long | 长定点格式.对double类型变量显示小数点后15位,对float类型变量显示小数点后7位. | 3.141592653589793 |
shortE | 短科学计数法,显示小数点后4位.并带有科学计数法标记. | 3.1416e+00 |
longE | 长科学计数法.对double类型变量显示小数点后15位,对float类型变量显示小数点后7位.并带有科学计数法标记. | 3.141592653589793e+00 |
bank | 银行格式.显示小数点后2位. | 3.14 |
hex | 十六进制格式. | 400921fb54442d18 |
rat | 比例格式 | 355/113 |
MATLAB命令行
-
使用行尾
;抑制输出: 在一行命令后使用;抑制输出,否则运算结果将被显示在终端上. -
其他实用的命令:
命令 作用 clc清除终端的输出 clear清除当前工作区内所有变量 who以简略格式显示工作区内所有变量 whos以复杂格式显示工作区内所有变量
使用MATLAB进行数字运算
使用MATLAB计算数学表达式
- MATLAB常见运算符有:
+,-,*,/,^. - 数学表达式被计算后,其值被存入变量
ans. - 运算的优先级规则:
- 同等优先级下从左向右运算.
- 优先级顺序(从高到低)
- 括号
() - 乘方
^ - 乘除法
*,/ - 加减法
+,-
- 括号
下面例子演示了数学表达式求值:
| 待求数学表达式 | MATLAB命令 |
|---|---|
| cos ( ( 1 + 2 + 3 + 4 ) 3 5 ) \cos\left(\sqrt{\frac{{\left(1+2+3+4\right)}^3}{5}}\right) cos(5(1+2+3+4)3) | cos(sqrt((1+2+3+4)^3/5)) |
| sin ( π ) + ln ( tan ( 1 ) ) \sin\left(\sqrt{\pi}\right) + \ln\left(\tan\left(1\right)\right) sin(π)+ln(tan(1)) | sin(sqrt(pi))+log(tan(1)) |
| 2 3.5 × 1.7 2^{3.5 \times 1.7} 23.5×1.7 | 2^(3.5*1.7) |
| e sin ( 10 ) e^{\sin(10)} esin(10) | exp(sin(10)) |
MATLAB内置的数学函数
- MATLAB内置的算数运算函数
- 基本运算:
- 加:
+,sum,cumsum,movsum - 减:
-,diff - 乘:
.*,*,prod,cumprod - 除:
./,.\,/,\ - 乘方:
.^,^
- 加:
- 取模运算:
mod,rem,idivide,ceil,fix,floor,round
- 基本运算:
- MATLAB内置的三角运算函数
- 正弦:
sin,sind,sinpi,asin,asind,sinh,asinh - 余弦:
cos,cosd,cospi,acos,acosd,cosh,acosh - 正切:
tan,tand,atan,atand,atan2,atan2d,tanh,atanh - 余割:
csc,cscd,acsc,acscd,csch,acsch - 正割:
sec,secd,asec,asecd,sech,asech - 余切:
cot,cotd,acot,acotd,coth,acoth - 斜边:
hypot - 转换:
deg2rad,rad2deg,cart2pol,cart2sph,pol2cart,sph2cart
- 正弦:
- MATLAB内置的指数对数函数:
exp,expm1,log,log10,log1p,log2,nextpow2,nthroot,pow2,reallog,realpow,realsqrt,sqrt - MATLAB内置的复函数:
abs,angle,complex,conj,cplxpair,i,imag,isreal,j,real,sign,unwrap
使用MATLAB进行矩阵运算
定义矩阵
向终端输入矩阵
在MATLAB中,使用[]将待输入的矩阵内容括起来,使用空格或逗号,分隔行内变量,使用;分隔每一行.
下面例子演示了矩阵的定义:
| MATLAB命令 | 得到的矩阵 |
|---|---|
[1 2 3 4] | [ 1 2 3 4 ] \left[\begin{array}{cccc} 1 & 2 & 3 & 4 \end{array}\right] [1234] |
[1; 2; 3; 4] | [ 1 2 3 4 ] \left[\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}\right] ⎣⎢⎢⎡1234⎦⎥⎥⎤ |
[1 21 6; 5 17 9; 31 2 7] | [ 1 21 6 5 17 9 31 2 7 ] \left[\begin{array}{ccc} 1 & 21 & 6 \\ 5 & 17 & 9 \\ 31 & 2 & 7\end{array}\right] ⎣⎡153121172697⎦⎤ |
使用冒号运算符创建向量
使用冒号运算符:可以创建一个长向量,其语法如下:
| 冒号表达式 | 得到的结果 |
|---|---|
j:k | [ j , j + 1 , j + 2 , . . . , j + m ] \left[\begin{array}{ccccc} j ,& j+1, & j+2, & ... ,& j+m \end{array}\right] [j,j+1,j+2,...,j+m] |
j:i:k | [ j , j + i , j + 2 i , . . . , j + m ∗ i ] \left[\begin{array}{ccccc} j, & j+i, & j+2i, & ..., & j+m*i \end{array}\right] [j,j+i,j+2i,...,j+m∗i] |
下面例子演示了冒号运算符的使用:
| MATLAB语句 | 得到的结果 |
|---|---|
1:5 | [ 1 2 3 4 5 ] \left[\begin{array}{cccc} 1 & 2 & 3 & 4 & 5\end{array}\right] [12345] |
1:2:5 | [ 1 3 5 ] \left[\begin{array}{cccc} 1 & 3 & 5\end{array}\right] [135] |
[1:5; 2:3:15; -2:0.5:0] | [ 1 2 3 4 5 2 5 8 11 14 − 2 − 1.5 − 1 − 0.5 0 ] \left[\begin{array}{cccc} 1 & 2 & 3 & 4 & 5 \\ 2 & 5 & 8 & 11 & 14 \\ -2 & -1.5 & -1 & -0.5 & 0\end{array}\right] ⎣⎡12−225−1.538−1411−0.55140⎦⎤ |
'a':2:'z' | 'acegikmoqsuwy' |
定义特殊矩阵
下列命令可以定义特殊矩阵
| 命令 | 得到的结果 |
|---|---|
eye(n) | 得到一个 n × n n\times n n×n的单位矩阵 |
zeros(n1, n2) | 得到一个 n 1 × n 2 n_1 \times n_2 n1×n2的全0矩阵 |
ones(n1, n2) | 得到一个 n 1 × n 2 n_1 \times n_2 n1×n2的全1矩阵 |
diag(vector) | 得到一个以向量vector中内容为对角线的对角矩阵 |
矩阵的索引
-
MATLAB中的矩阵是以列先序存储的.且索引下标从1开始.
-
矩阵有两种索引方式: 按一维索引和按二维索引.对于一个一般的矩阵,其索引顺序如下:
[ 1 或 ( 1 , 1 ) 4 或 ( 1 , 2 ) 7 或 ( 1 , 3 ) 2 或 ( 2 , 1 ) 5 或 ( 2 , 2 ) 8 或 ( 2 , 3 ) 3 或 ( 3 , 1 ) 6 或 ( 3 , 2 ) 9 或 ( 3 , 3 ) ] \left[\begin{array}{ccc} 1或(1,1) & 4或(1,2) & 7或(1,3) \\ 2或(2,1) & 5或(2,2) & 8或(2,3) \\ 3或(3,1) & 6或(3,2) & 9或(3,3) \end{array}\right] ⎣⎡1或(1,1)2或(2,1)3或(3,1)4或(1,2)5或(2,2)6或(3,2)7或(1,3)8或(2,3)9或(3,3)⎦⎤ -
矩阵的索引可以使用冒号
:,表示选取所有行或所有列. -
矩阵的索引可以是一个或两个向量,表示选中向量内的所有行或所有列.
下面例子演示了矩阵索引的规则:
| 原矩阵 | 索引 | 得到的结果 | 解释 |
|---|---|---|---|
| A = [ 1 2 3 4 5 6 7 8 9 ] A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right] A=⎣⎡147258369⎦⎤ | A(8) | 6 6 6 | 取矩阵第8个元素 |
| A = [ 1 2 3 4 5 6 7 8 9 ] A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right] A=⎣⎡147258369⎦⎤ | A([1 3 5]) | [ 1 7 5 ] \left[\begin{array}{ccc} 1 & 7 & 5 \end{array}\right] [175] | 分别取矩阵第[1 3 5]个元素放入新矩阵的对应位置 |
| A = [ 1 2 3 4 5 6 7 8 9 ] A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right] A=⎣⎡147258369⎦⎤ | A([1 2; 3 4]) | [ 1 4 7 2 ] \left[\begin{array}{ccc} 1 & 4 \\ 7 & 2 \end{array}\right] [1742] | 分别取矩阵第[1 2; 3 4]个元素放入新矩阵的对应位置 |
| A = [ 1 2 3 4 5 6 7 8 9 ] A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right] A=⎣⎡147258369⎦⎤ | A(3,2) | 8 8 8 | 取矩阵第3行第2列的元素 |
| A = [ 1 2 3 4 5 6 7 8 9 ] A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right] A=⎣⎡147258369⎦⎤ | A([1,2], :) | [ 1 2 3 4 5 6 ] \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right] [142536] | 取矩阵第[1 2]行和所有列的交叉项 |
| A = [ 1 2 3 4 5 6 7 8 9 ] A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right] A=⎣⎡147258369⎦⎤ | A([1 3], [1 2]) | [ 1 2 7 8 ] \left[\begin{array}{ccc} 1 & 2 \\ 7 & 8 \end{array}\right] [1728] | 取矩阵第[1 3]行和第[1 2]列的交叉项 |
矩阵的操作
操作矩阵的运算符
| 运算符 | 操作 | 形式 | 例子 |
|---|---|---|---|
+ | 矩阵与向量相加 | A+b | [6 3] + 2 = [8 5] |
- | 矩阵与向量相减 | A-b | [6 3] - 2 = [4 1] |
+ | 矩阵与矩阵对应位置相加 | A+B | [6 3] + [4 8] = [10 11] |
- | 矩阵与矩阵对应位置相减 | A-B | [6 3] - [4 8] = [2 -5] |
* | 矩阵与矩阵相乘 | A*B | [6 3] * [4 8]' = 48 |
.* | 矩阵与矩阵对应位置相乘 | A.*B | [6 3] * [4 8] = [24 24] |
/ | 矩阵与矩阵右除(等价于A*inv(B)) | A/B | [6 3] / [4 8] = 0.6 |
\ | 矩阵与矩阵左除(等价于inv(A)*B) | A\B | [6 3] / [4 8] = [0.06667 1.3333; 0 0] |
./ | 矩阵与矩阵对应位置右除 | A./B | [6 3] ./ [4 8] = [1.5 0.375] |
.\ | 矩阵与矩阵对应位置左除 | A.\B | [6 3] .\ [4 8] = [0.6667 2.6667] |
^ | 矩阵与向量乘方 | A^b | [1 2; 3 4]^3 = [37 54; 81 118] |
.^ | 矩阵与矩阵对应位置乘方 | A.^B | [1 2; 3 4].^[1 2; 3 4] = [1 4; 27 256] |
操作矩阵的函数
下面对矩阵
A
=
[
1
2
3
0
5
6
7
0
9
]
A = \left[\begin{array}{ccc} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 7 & 0 & 9 \end{array}\right]
A=⎣⎡107250369⎦⎤
进行操作以演示操作矩阵的常见函数
| 函数 | 作用 | 例子 | 结果 |
|---|---|---|---|
max(A, [], dim) | 获取矩阵A的dim维度上的最大值 | max(A, [], 1) | [ 7 5 9 ] \left[\begin{array}{ccc} 7 & 5 & 9 \end{array}\right] [759] |
min(A, [], dim) | 获取矩阵A的dim维度上的最小值 | min(A, [], 2) | [ 1 0 0 ] \left[\begin{array}{ccc} 1 \\ 0 \\ 0 \end{array}\right] ⎣⎡100⎦⎤ |
sum(A, dim) | 获取矩阵A的dim维度上的和 | sum(A, 1) | [ 8 7 18 ] \left[\begin{array}{ccc} 8 & 7 & 18 \end{array}\right] [8718] |
mean(A, dim) | 获取矩阵A的dim维度上的平均值 | mean(A, 1) | [ 2.6667 2.3333 6.0000 ] \left[\begin{array}{ccc} 2.6667 & 2.3333 & 6.0000 \end{array}\right] [2.66672.33336.0000] |
sort(A, dim, direction) | 获取矩阵A的dim维度上按direction顺序排序结果 | sort(A, 1, 'descend') | [ 7 5 9 1 2 6 0 0 3 ] \left[\begin{array}{ccc} 7 & 5 & 9 \\ 1 & 2 &6 \\ 0 & 0 & 3 \end{array}\right] ⎣⎡710520963⎦⎤ |
sortrows(A, column) | 获取矩阵A按照每行第column个元素升序排序结果. | sortrows(A, 2) | [ 7 0 9 1 2 3 0 5 6 ] \left[\begin{array}{ccc} 7 & 0 & 9 \\ 1 & 2 & 3 \\ 0 & 5 & 6 \end{array}\right] ⎣⎡710025936⎦⎤ |
size(A, dim) | 获取矩阵A的dim维度上的形状.若不指定dim,则返回整个矩阵的形状. | size(A) | [ 3 3 ] \left[\begin{array}{ccc} 3 & 3 \end{array}\right] [33] |
find(A, n) | 获取矩阵A前n个非零元素的索引 | find(A,5) | [ 1 3 4 5 7 ] \left[\begin{array}{ccc} 1 & 3 & 4 & 5 & 7 \end{array}\right] [13457] |
对于上面这些函数,除第一个参数以外,其它参数都是可选的.
pdf版本笔记的下载地址: MATLAB01_基本的数学运算与矩阵运算(访问密码:3834)