MATLAB02:结构化编程和函数定义

pdf版本笔记的下载地址: MATLAB02_结构化编程和函数定义（访问密码：3834）

MATLAB02:结构化编程和函数定义

结构化编程
函数

学习一门技术最好的方式就是阅读官方文档,可以查看MATLAB官方文档

结构化编程

流程控制语句和逻辑运算符

与大多数编程语言相同,MATLAB有以下流程控制语句:

流程控制语句	作用
`if, elseif, else`	若`if`语句为真,则执行子句
`switch, case, otherwise`	根据`switch`语句内容判断执行哪个子句
`while`	重复执行子句直到`while`中的条件为假
`for`	执行子句固定次数
`try, catch`	执行子句并捕获执行过程中的异常

`break`	跳出循环
`continue`	直接进入下一次循环
`end`	结束子句
`pause`	暂停程序
`return`	返回到调用函数处

上述所有循环和条件语句都要在末尾以end闭合.

MATLAB还有以下逻辑运算符:

运算符	意义
`<`	小于
`<=`	小于或等于
`>`	大于
`>=`	大于或等于
`==`	等于
`~=`	不等于
`&&`	且
`\|\|`	或

&&和||运算符支持逻辑短路功能.

流程控制语句示例

下面演示各流程控制语句:

if语句:

if语句的用法

if rem(a, 2) == 0
	disp('a is even');
else
	disp('a is odd');
end

switch语句:

switch语句的用法

switch input_num
case -1
	disp('negative 1');
case 0
	disp('zero');
case 1
	disp('positive 1');
otherwise
	disp('other value');
end

while语句:

while语句的用法

n = 1;
while prod(1:n) < 1e100
	n = n + 1;
end

for语句:
```
for n=1:10
	a(n)=2^n;
end
disp(a)
```

break语句:

x = 2; k = 0; error = inf;
error_threshold = 1e-32;
while error > error_threshold
    if k > 100
    	break
    end
    x = x - sin(x)/cos(x);
    error = abs(x - pi);
    k = k + 1;
end

使用循环语句应尽量预先分配内存空间

若一个变量所需要的内存空间是一个可预测的定值,我们应尽量提前为其分配内存空间.

以下面两段程序为例,演示这一点:

程序一:

tic
for ii = 1:2000
    for jj = 1:2000
        A(ii,jj) = ii + jj;
    end
end
toc

程序输出Elapsed time is 4.616199 seconds.

程序二:

tic
A = zeros(2000, 2000);		% 预先为变量分配内存空间
for ii = 1:size(A,1)
    for jj = 1:size(A,2)
        A(ii,jj) = ii + jj;
    end
end
toc

程序输出Elapsed time is 2.786401 seconds.

可以看到,程序一比程序二所用的时间更长.这是因为: 对于程序一,没有预先为变量A分配内存,因此每当A的形状发生改变时,都需要重新为A分配内存地址,这花费了更多的时间.

编写脚本时应注意的问题

在脚本开头应添加语句清空工作区

在每个脚本的开头,应添加下述语句,清空工作区缓存以及之前程序运行的痕迹:

clear all	% 清空工作区内存中的变量
close all 	% 关闭之前程序绘制的图像
clc			% 清空之前程序在终端的输出

在运算和赋值语句后应添加分号`;`抑制输出

在所有运算和赋值语句都应该添加分号;抑制输出,若需要向终端输出一个变量,应对其调用disp方法.

使用省略号`...`拼接多行语句

在MATLAB中,省略号...可以将多行语句拼接为一行,灵活使用该语句可以提高代码可读性.

annPoints_sampled = annPoints(annPoints(:,1)>x1 & ...
    annPoints(:,1) < x2 & ...
    annPoints(:,2) > y1 & ...
    annPoints(:,2) < y2);

函数

与其他语言相似,MATLAB也可以定义函数.与脚本类似,函数可以被存入函数名.m文件中,也可以以函数句柄的形式定义在内存中.

查看内置函数

我们可以使用which命令查看内置函数源代码文件的位置,与edit命令结合可以查看内置函数的源代码.

运行下面语句可以打开MATLAB内置的mean函数的源文件:

edit(which('mean.m'))

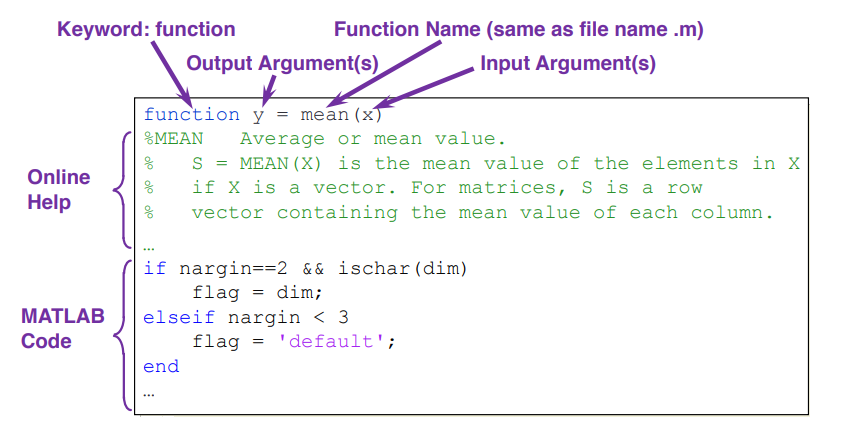
可以在编辑器中看到mean函数的源代码如下:

mean函数源代码

以`函数名.m`文件形式定义函数

在MATLAB文件中定义函数的格式如下:

function [输出变量名] = 函数名(输入变量名) 
% 函数的文档

函数代码

function是一个关键字,声明该文件中保存的是一个函数.
输入变量和输出变量是非必须的,函数既可以没有输入变量,也可以没有输出变量.
函数名应与.m文件名相同,且不包含特殊字符(最好不要有中文).

MATLAB内置的函数参数

在MATLAB中,内置了一些函数参数如下:

函数参数	意义
`imputname`	输入变量名列表
`mfilename`	函数源代码文件名
`nargin`	输入变量数
`nargout`	输出变量个数
`varargin`	可变长输入参数列表
`varargout`	可变长输出参数列表

MATLAB不提供其他高级语言的指定默认参数值以及函数重载等语法,但灵活使用上述内置的函数参数,可以在一定程度上实现指定默认参数值以及方法重载:

function [volume]=pillar(Do,Di,height)
if nargin==2,
	height=1;
end
volume=abs(Do.^2-Di.^2).*height*pi/4;

MATLAB函数定义示例1

下面程序用来计算自由落体运动中位移量:
$x_0 + v_0 t + \frac{1}{2} g t^2$

function x = freebody(x0,v0,t)
% calculation of free falling
% x0: initial displacement in m
% v0: initial velocity in m/sec
% t: the elapsed time in sec
% x: the depth of falling in m
x = x0 + v0.*t + 1/2*9.8*t.*t;

该函数演示了一个MATLAB编程技巧: 计算乘法时应尽量使用.*而非*,因为前者不仅对参数t为标量的情况可用,也对变量t为向量或矩阵的情况可用.

freebody(0, 0, 2)			% 得到 19.6000
freebody(0, 0, [0 1 2 3])	% 得到 [0 4.9000 19.6000 44.1000]
freebody(0, 0, [0 1; 2 3])	% 得到 [0 4.9000; 19.6000 44.1000]

MATLAB函数定义示例2

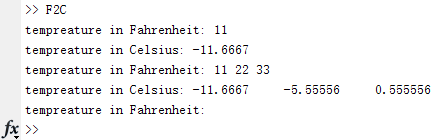
下面函数实现了从华氏温度到摄氏温度的转换,该函数可以识别输入的待转换样例的个数,当输入的待转换样例个数为0时,退出函数.

function F2C()
while 1
    F_degree = input('tempreature in Fahrenheit: ', 's');
    F_degree = str2num(F_degree);
    if isempty(F_degree)
        return
    end
    C_degree = (F_degree-32)*5/9;
    disp(['tempreature in Celsius: ' num2str(C_degree)])
end

F2C函数执行结果
(需要按Ctrl+C退出程序)

以函数句柄形式定义函数

我们也可以使用函数句柄的形式定义函数,这更接近数学上的函数定义,其语法如下:

函数句柄 = @(输入变量) 输出变量

可以直接通过函数句柄调用该方法.

f = @(x) exp(-2*x);
x = 0:0.1:2;
plot(x, f(x));

pdf版本笔记的下载地址: MATLAB02_结构化编程和函数定义（访问密码：3834）