Kmeans

Kmeans属于无监督学习 对输入样本不断地迭代 计算出最佳质心

步骤
1、随机选定k个样本作为质心
2、开始循环
2.1、将各个样本点分配到离它们最近的质心，生成k个簇
2.2、对于每个簇，计算所有被分到该处的样本点的平均值作为新的质心
3、当质心位置不再变化时，迭代停止，完成聚类。

簇内误差的定义
i 表示每个样本的第i个特征
x表示样本 μ表示质心
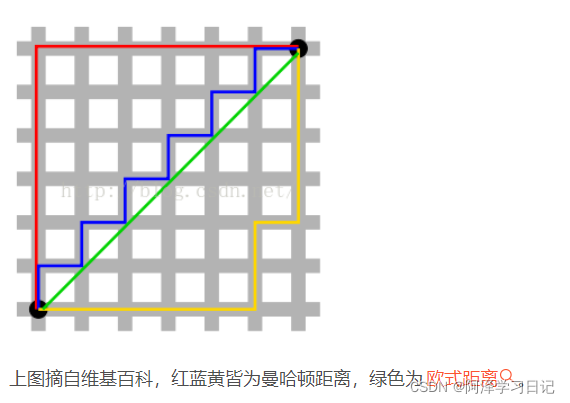
欧几里得距离
d = 根号∑(xi-μi)^2
曼哈顿距离
d = ∑|xi-μi|
欧几里得距离是类似于勾股定理 求两点之间的最短距离（直线） 而 曼哈顿距离也叫”曼哈顿街区距离”。想象你在曼哈顿街道上，从一个十字路口开车到另一个十字路口，驾驶距离就是这个“曼哈顿距离”。

一个簇中各个样本的距离平方和、所有簇各个样本达到各自簇的距离分别为

注意Kmeans、Knn均为损失函数，无需计算参数，只有调试超参数

重要参数以及评估指标

n_clusters
分的簇的数目
tip当数据太多时，可以对数据进行切片，先KMeans()f.it(x[:1000])得到一个较好的质心
再predict(X) （在上文fit的质心基础上，直接将X数据集分到各个簇中）

init
初试样本点的找寻方式 ‘k-means++’(default，会尽量让各个点距离分开一些) ‘random’ (随机找)
KMeans.n_iter_ 返回迭代次数
n_init
用不同的质心初始化值运行算法的次数

max_iter 和 tol
最大迭代次数 不一定迭代max_iter次 提前收敛会终止
tol 两次得带之间的inertia下降至小于tol 会终止迭代

评估指标
inertia
随着n_cluster变大 inertia会下降 但由于inertia无边界 容易受特征数目的影响
客观性不行
轮廓系数
较为客观
a：该点到簇内其他店的平均距离(相似度)
b: 该点到其他最近簇的所有样本点之间的平均距离
s = (b-a)/max(a,b)

s=1-a/b (a<b) 0 (a=b) b/a-1(b>a)
s范围（-1,1）
s^较大时，说明聚类效果好 越接近1越好
s^趋近于0时，说明两个簇相似度极其高，应属于同一簇
若s^较小或者为负数，说明超参数k过大或者过小
库
metric.silhouette_score 来计算轮廓系数（均值）
metric.silhouette_sample 每个样本的轮廓系数

重要接口
cluster_centers_
返回质心
labels_
每个样本对应的标签
inertia_ 粗内平方和
n_iter_ 迭代次数
接口
fit 拟合
fit_predict 返回拟合模型对输入样本的簇的估计
get_params 获得该类的参数
score 返回 -inertia
set_params 重设参数

Kmeans适用场景
常用于非结构数据的矢量量化
矢量量化是指在同样样本量的情况下压缩信息的大小(适用代表性信息替代其他信息 如质心)

一些新学的函数

ax.fill_betwwenx() 是将范围内的柱状图都同一颜色的函数
ax.text(position_x,position_y,文本信息)