从等差数列到杨辉三角,再到N阶等差数列，请准备好水，这一期干货满满，脑洞大开，超级炸裂，Let's Go！！！

这次我们从大家十分熟悉的的等差数列开始

一阶等差数列（Arithmetic Sequence）：

这是我们最熟悉的函数，要用递归函数求取他的各个值，我们先要知道它的递推关系

F(N)=F(N-1)+A

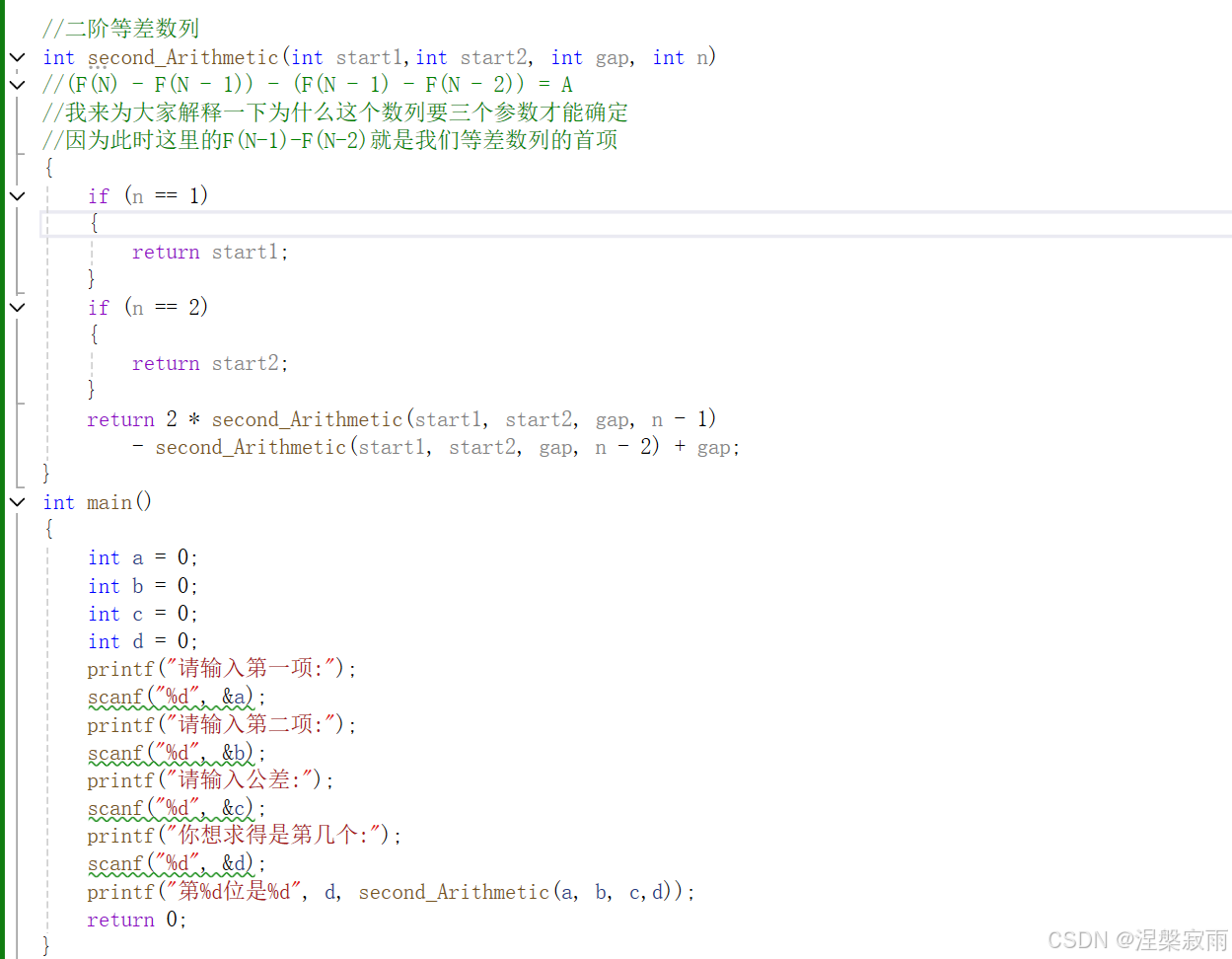
二阶等差数列 （second-order arithmetic sequence）

就是差的差是一个定值

(F(N)-F(N-1))-(F(N-1)-F(N-2))=A<<<<=====>>>>F(N)=2×F(N-1)-F(N-2)+A

OK，让我们继续深入

N阶等差数列 

OK，为了帮助大家理解，我们现在来看一下三阶等差数列

三阶等差数列

他的递推公式为

（(F(N)-F(N-1))-(F(N-1)-F(N-2))）-（(F(N-1)-F(N-2))-(F(N-2)-F(N-3))）=A<<<=====>>>

(F(N)-2×F(N-1)+F(N-2))-(F(N-1)-2×F(N-2)+F(N-3))=A<<<====>>>F(N)-3×F(N-1)+3×F(N-2)-F(N-3)=A

而三阶等差数列我们就需要四个参数来帮助我们确定这个三阶等差数列

现在我们把从一到三阶的等差数列全部呈现出来

一阶：                                        F(N)-F(N-1)=A

二阶：                                F(N)-2×F(N-1)+F(N-2)=A

三阶：                         F(N)-3×F(N-1)+3×F(N-2)-F(N-3)=A

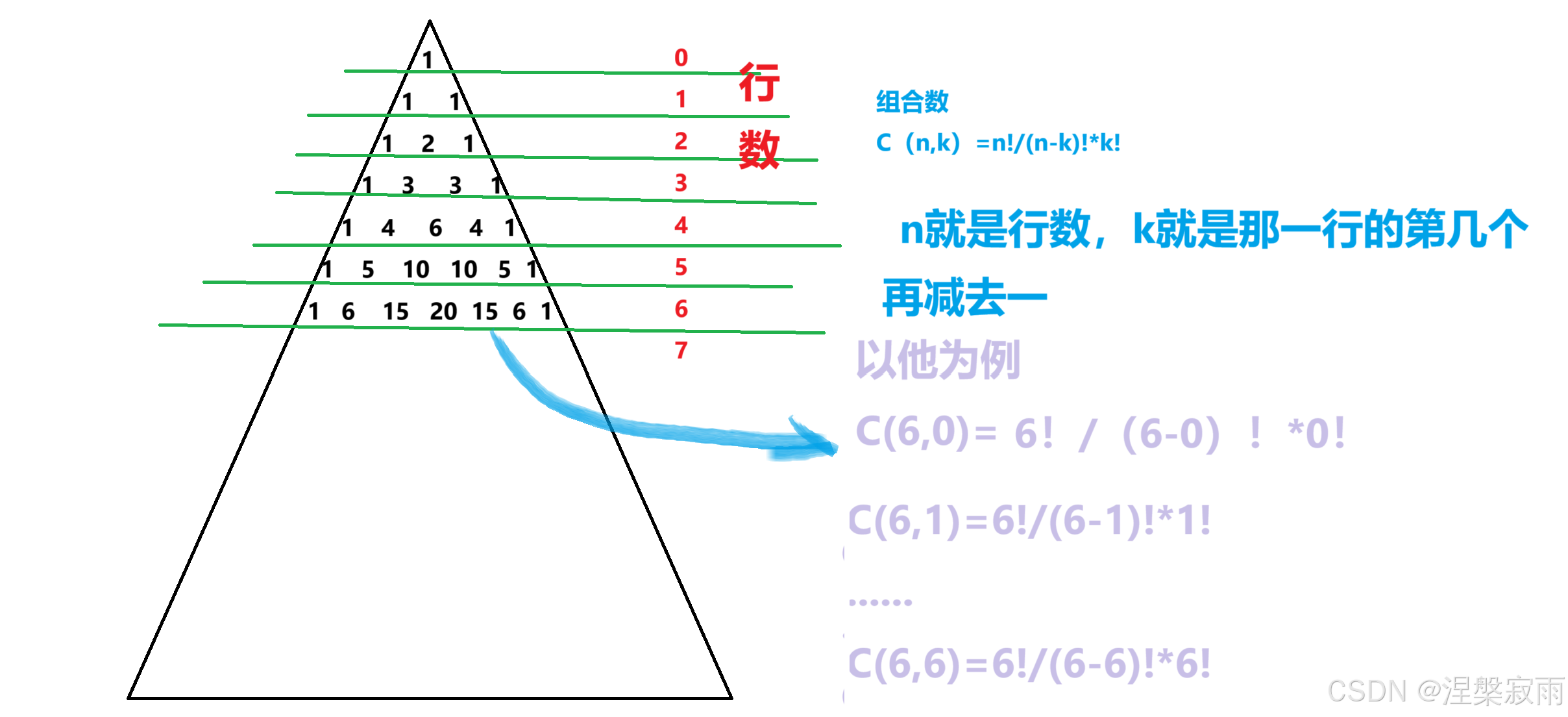
OK，讲到这里，相信对杨辉三角（或者帕斯卡三角）的朋友们已经有所察觉，没错，他们的递推公式的系数其实是一个杨辉三角的变种，即在杨辉三角的基础之上每个系数再乘（-1）^n-1，OK，解开了这一层神秘的面纱之后，想要编译一个高阶的等差数列，我们就先要了解杨辉三角

支线任务——杨辉三角

所以，我们先写一个组合数的函数，用于计算杨辉三角的系数，Let's go!!!

int factorial(int n)
{
	if (n == 1 ||n==0)
	{
		return 1;
	}
	return n * factorial(n - 1);
}

 先写一个计算阶乘的函数，因为后面会频繁用到阶乘

接下来是计算杨辉三角的函数，我们需要行数，和第几个这两个参数

int YHtriangle(int n, int k)
{
	int a = factorial(n);
	int b = factorial(n - k);
	int c = factorial(k);
	return a / (b * c);
}

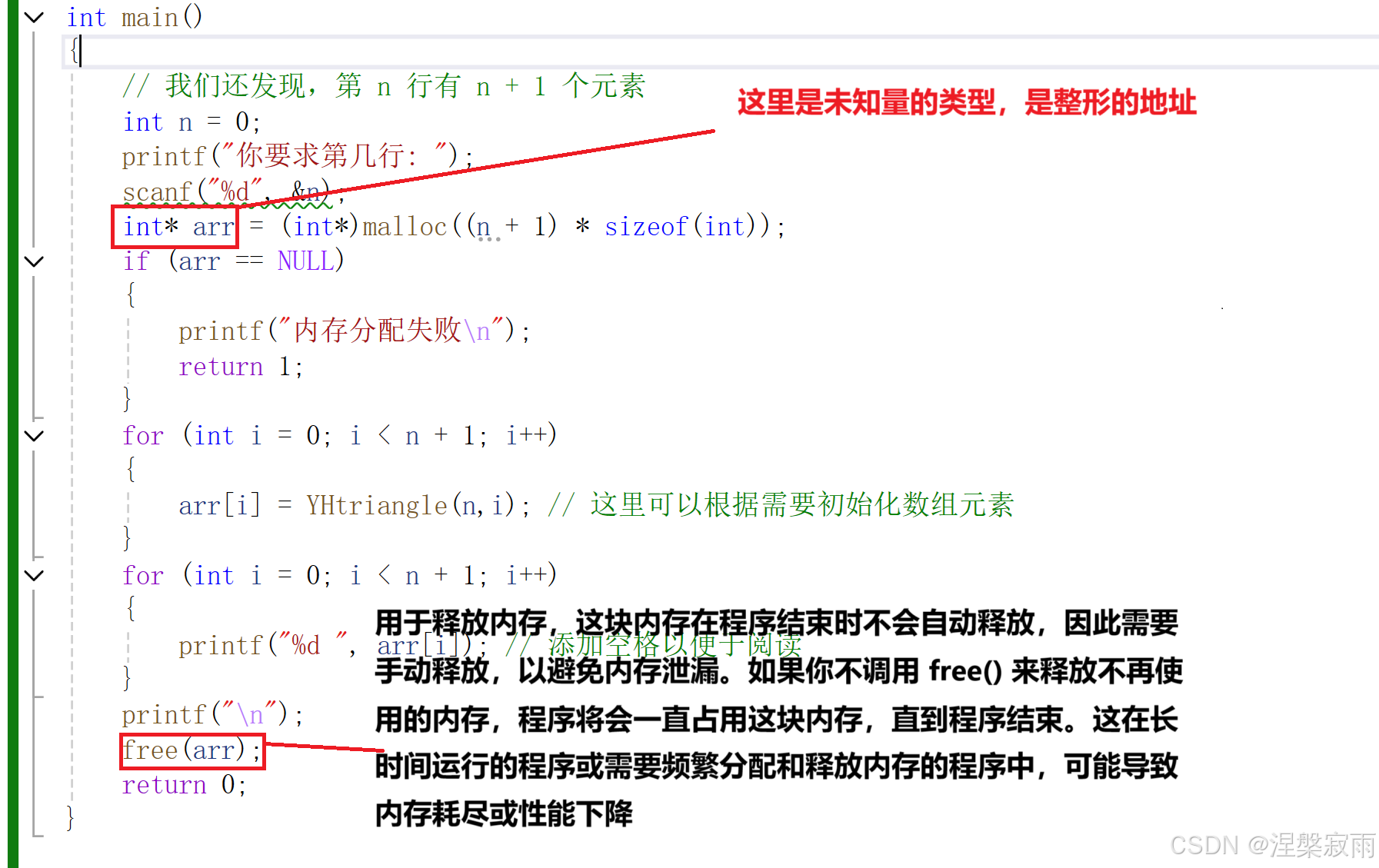
OK，最后，我们需要创建一个可变数组（就是他的元素的个数是可以改变的数组），因为我们在定义数组时，填入的个数必须是常量，不能是变量，那怕是被constant修饰过的也不行，所以我们采用动态分配内存的方法，要使用malloc函数

OK，先来介绍一下malloc函数

他是C 语言中用于动态内存分配的标准库函数，使用 malloc 可以在程序运行时动态地分配一块指定大小的内存，而不是在编译时就确定内存的大小，它需要的参数是是需要分配的内存大小（是以字节为单位），所以我们还需要调用sizeof函数来计算大小，malloc是一个有返回值的函数，他的返回值是，返回一个指向分配内存的指针，如果分配失败则返回NULL，所以他返回的是一个指针，那么我们就要用指针变量来接收他的返回值

OK，接下来请看演示

int main()
{
    // 我们还发现，第 n 行有 n + 1 个元素
    int n = 0;
    printf("你要求第几行: ");
    scanf("%d", &n);
    int* arr = (int*)malloc((n + 1) * sizeof(int));
    if (arr == NULL) 
    {
        printf("内存分配失败\n");
        return 1; 
    }
    for (int i = 0; i < n + 1; i++)
    {
        arr[i] = YHtriangle(n,i); // 这里可以根据需要初始化数组元素
    }
    for (int i = 0; i < n + 1; i++)
    {
        printf("%d ", arr[i]); // 添加空格以便于阅读
    }
    printf("\n"); 
    free(arr);
    return 0;
}

OK，现在我们已经可以获取杨辉三角任意的一行的系数了，不过我们还要有一点改动，再乘上（-1）**i

请看

好的，解决了杨辉三角这个支线任务，让我们回到我们的主线任务

主线任务——N阶等差数列

根据前面的推导，我们可以知道，第N阶对应的就是我们的第N行杨辉三角的系数，在实际计算时，我们要做移项工作，所以系数也要再乘以-1

由于N阶等差数列是一个所需要的参数是N+1个，如果让使用者来填写，显然不合适，于是，我假设N阶等差数列的前N项分别为1，2,3.......，就是他们的序列号，而使用者需要填写的有，阶数，公差，第几项，之后就可以交给我们的算法去完成

阶乘

组合数 

杨辉三角

N阶等差数列 

以下是该函数的所有代码

int YHtriangle(int n, int k) 
{
    int a = factorial(n);
    int b = factorial(n - k);
    int c = factorial(k);
    return a / (b * c);
}





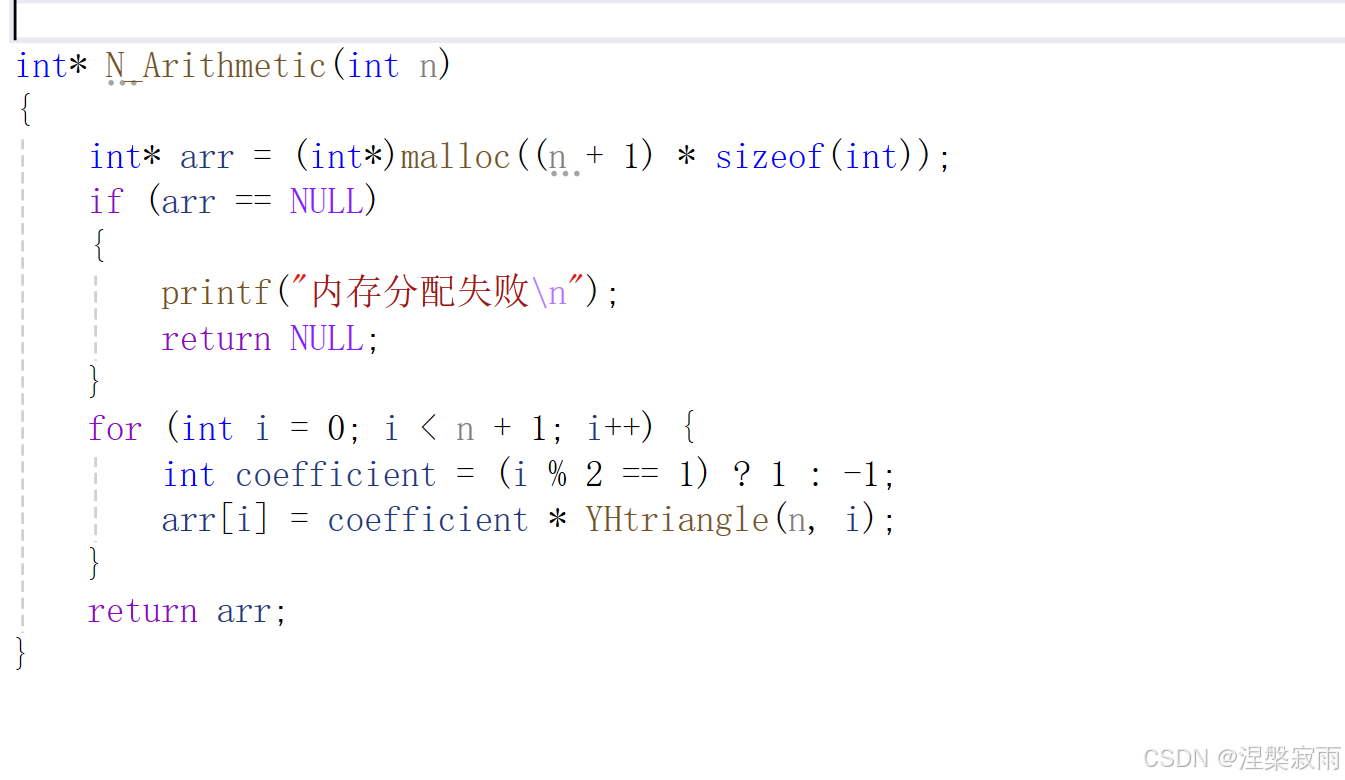
int* N_Arithmetic(int n)
{
    int* arr = (int*)malloc((n + 1) * sizeof(int));
    if (arr == NULL) 
    {
        printf("内存分配失败\n");
        return NULL;
    }
    for (int i = 0; i < n + 1; i++) 
    {
        int coefficient = (i % 2 == 1) ? 1 : -1;
        arr[i] = coefficient * YHtriangle(n, i);
    }
    return arr;
}



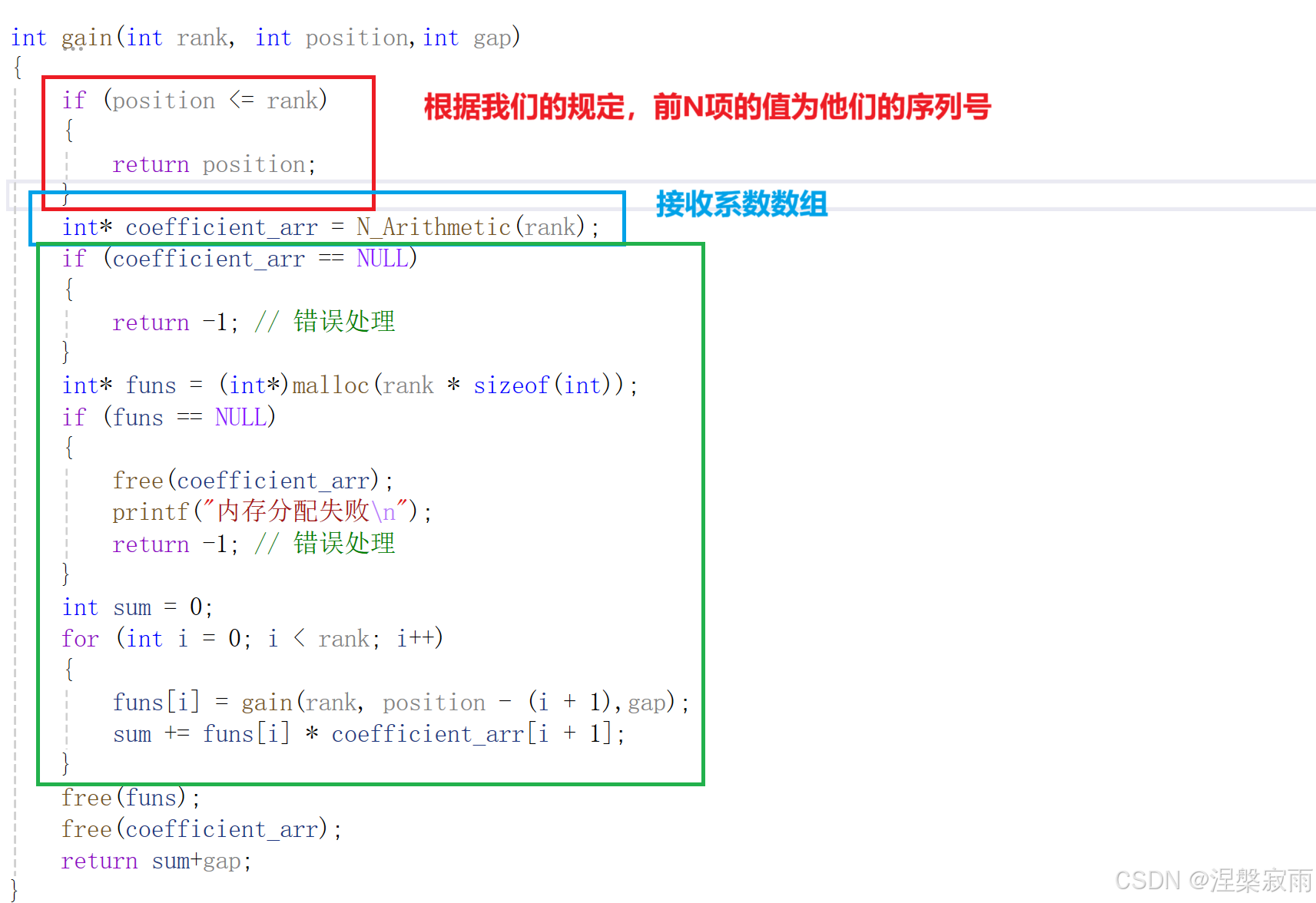
int gain(int rank, int position,int gap) 
{
    if (position <= rank) 
    {
        return position;
    }
    int* coefficient_arr = N_Arithmetic(rank);
    if (coefficient_arr == NULL) 
    {
        return -1; // 错误处理
    }
    int* funs = (int*)malloc(rank * sizeof(int));
    if (funs == NULL) 
    {
        free(coefficient_arr);
        printf("内存分配失败\n");
        return -1; // 错误处理
    }
    int sum = 0;
    for (int i = 0; i < rank; i++) 
    {
        funs[i] = gain(rank, position - (i + 1),gap);
        sum += funs[i] * coefficient_arr[i + 1];
    }
    free(funs);
    free(coefficient_arr);
    return sum+gap;
}



int main() 
{
    int a = 0;
    int b = 0;
    int c = 0;
    printf("几阶等差数列：");
    scanf("%d", &a);
    printf("公差：");
    scanf("%d", &c);
    printf("第几项：");
    scanf("%d", &b);
    int result = gain(a, b, c);
    printf("结果是%d\n", result);
    return 0;
}

 怎么样，是不是收获了一个充满智慧的大脑，来吧，和我一起探索编程的更多有意思的玩法