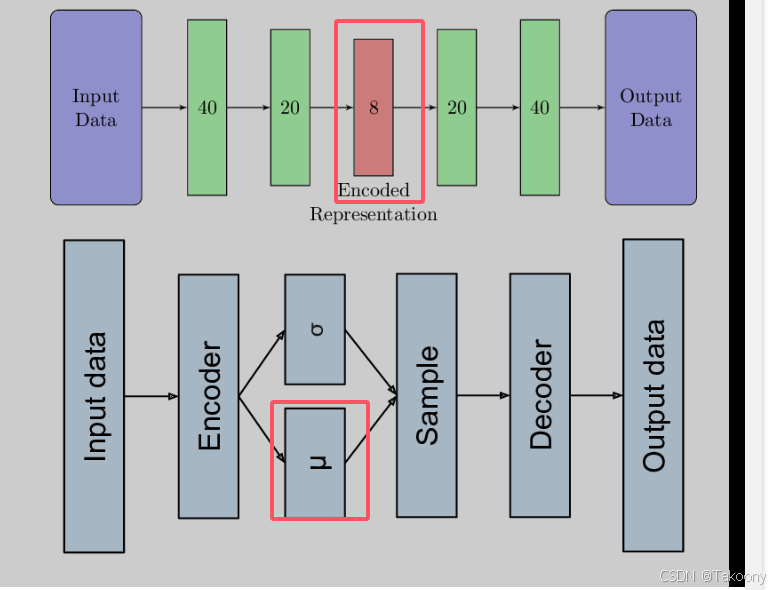
模型结构

案例说明

为了更好地理解变分自编码器（VAE）和自编码器（AE）的区别，让我们通过一个具体的例子来说明。假设我们正在处理一个手写数字图像数据集，如 MNIST。

例子：手写数字识别和生成

自编码器（AE）
结构和功能：

输入：28x28 像素的手写数字图像
编码器：将图像压缩到 10 维潜在空间
解码器：将 10 维潜在表示重建为原始图像尺寸
训练过程：
	目标：最小化重建误差
	损失函数：均方误差（MSE）
使用场景：
	数据压缩：将 784 维（28x28）的图像压缩到 10 维
	去噪：输入带噪声的图像，输出清晰图像
	特征提取：使用编码器输出作为图像的特征表示
局限性：
	不能自然地生成新的手写数字图像
	潜在空间可能不连续，相邻点可能对应完全不同的数字

变分自编码器（VAE）
结构和功能：

输入：28x28 像素的手写数字图像
编码器：输出 10 维潜在空间的均值和方差
解码器：从潜在空间采样，重建原始尺寸图像
训练过程：
	目标：最大化变分下界（ELBO）
	损失函数：重建误差 + KL 散度
使用场景：
	生成新的手写数字图像
	数据插值：在潜在空间中平滑过渡，生成中间状态的数字
	条件生成：给定特定条件（如数字类别），生成对应的手写数字
优势：
	可以生成新的、多样化的手写数字图像
	潜在空间是连续的，相邻点对应相似的数字
	具体对比
	潜在空间采样：

AE：从潜在空间随机选择一点（如 [0.1, 0.5, …, 0.8]），直接输入解码器，可能得到不合理的输出。
VAE：从学习到的高斯分布中采样（如均值 [0.1, 0.5, …, 0.8]，方差 [0.01, 0.02, …, 0.01]），生成的图像更符合真实数字分布。
数字插值：

AE：在潜在空间中两点之间线性插值，可能产生不连续或不合理的过渡。
VAE：在潜在空间中平滑插值，能够生成从一个数字渐变到另一个数字的连续序列（如从 “2” 平滑过渡到 “7”）。
异常检测：

AE：主要依赖重建误差来检测异常。
VAE：可以利用重建误差和 KL 散度来更全面地检测异常，如识别出不符合学习到的数字分布的输入。
条件生成：

AE：不直接支持条件生成。
VAE：可以通过在潜在空间中加入条件信息（如数字类别），实现有控制的生成过程，例如生成特定数字的多种手写样式。
通过这个例子，我们可以看到 VAE 在生成任务和学习数据分布方面的优势，而 AE 则更适合用于数据压缩和重建任务。VAE 的概率性质使其能够捕捉数据的潜在结构，并生成新的、多样化的样本。

案例代码

# 首先，让我们导入必要的库并设置一些参数：
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

# 设置参数
batch_size = 128
epochs = 10
log_interval = 10
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
接下来，我们定义 VAE 模型：

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
        
        # 编码器
        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, 20)  # 均值
        self.fc22 = nn.Linear(400, 20)  # 对数方差
        
        # 解码器
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 784)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5*logvar)
        eps = torch.randn_like(std)
        return mu + eps*std

    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        return torch.sigmoid(self.fc4(h3))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 784))
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar
# 现在，我们定义损失函数和训练过程：

# 重建损失 + KL散度
def loss_function(recon_x, x, mu, logvar):
    BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return BCE + KLD

def train(epoch):
    model.train()
    train_loss = 0
    for batch_idx, (data, _) in enumerate(train_loader):
        data = data.to(device)
        optimizer.zero_grad()
        recon_batch, mu, logvar = model(data)
        loss = loss_function(recon_batch, data, mu, logvar)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()
        
        if batch_idx % log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader),
                loss.item() / len(data)))

    print('====> Epoch: {} Average loss: {:.4f}'.format(
          epoch, train_loss / len(train_loader.dataset)))
# 接下来，我们加载数据并训练模型：

# 加载MNIST数据集
train_loader = DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.ToTensor()),
    batch_size=batch_size, shuffle=True)

# 初始化模型和优化器
model = VAE().to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)

# 训练模型
for epoch in range(1, epochs + 1):
    train(epoch)
# 最后，我们可以使用训练好的模型生成新的数字图像：

def generate_images(model, num_images=10):
    with torch.no_grad():
        sample = torch.randn(num_images, 20).to(device)
        sample = model.decode(sample).cpu()
        return sample

# 生成并显示图像
generated = generate_images(model)
fig, axes = plt.subplots(1, 10, figsize=(20, 2))
for i, ax in enumerate(axes):
    ax.imshow(generated[i].view(28, 28), cmap='gray')
    ax.axis('off')
plt.show()

这个例子展示了 VAE 的基本实现和使用。通过训练这个模型，我们可以：

• 将 MNIST 图像编码到一个 20 维的潜在空间。
• 从这个潜在空间中采样，生成新的手写数字图像。
• 通过调整潜在空间的值，探索不同的手写数字风格。
  VAE 的优势在于它学习了一个连续的潜在空间，使得我们可以生成新的、多样化的图像，而不仅仅是重建已有的图像。这个特性使 VAE 在生成模型领域非常有用，可以应用于图像生成、数据增强、异常检测等多个场景。

vae不能像ae一样降维获得encoder向量吗

VAE 也可以用于降维并获得编码器向量，就像传统的自编码器（AE）一样。让我解释一下 VAE 在这方面的应用：

VAE 的降维能力
VAE 确实可以用于降维，而且在某些方面可能比传统的 AE 更有优势：

潜在空间表示：VAE 的编码器输出的是潜在空间的概率分布参数（通常是均值和方差），而不是直接的固定向量。

采样过程：通过从这个分布中采样，我们可以获得低维的潜在表示。

获取 VAE 的编码器向量
有几种方法可以从 VAE 获得类似 AE 的编码器向量：

a) 使用均值向量：
最简单的方法是直接使用 VAE 编码器输出的均值向量作为降维后的表示。这种方法忽略了方差，但在许多实际应用中效果很好。

b) 采样：
从编码器输出的分布中采样，获得一个具体的向量。这种方法引入了随机性，可能更好地捕捉数据的不确定性。

c) 多次采样平均：
从分布中多次采样，然后取平均值。这可以减少单次采样的随机性。

代码示例
以下是如何从之前的 VAE 模型中获取编码器向量的示例：

def get_latent_vector(model, data):
    model.eval()
    with torch.no_grad():
        # 获取均值和方差
        mu, logvar = model.encode(data.view(-1, 784))
        
        # 方法1：直接使用均值
        latent_vector_mean = mu
        
        # 方法2：采样
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        latent_vector_sampled = mu + eps * std
        
        # 方法3：多次采样平均（这里以5次为例）
        samples = []
        for _ in range(5):
            eps = torch.randn_like(std)
            samples.append(mu + eps * std)
        latent_vector_avg = torch.stack(samples).mean(dim=0)
        
    return latent_vector_mean, latent_vector_sampled, latent_vector_avg

# 使用示例
sample_data = next(iter(train_loader))[0][:10].to(device)  # 取10个样本
mean_vec, sampled_vec, avg_vec = get_latent_vector(model, sample_data)

print("均值向量形状:", mean_vec.shape)
print("采样向量形状:", sampled_vec.shape)
print("平均采样向量形状:", avg_vec.shape)

VAE 用于降维的优势

• 概率解释：VAE 提供了数据在潜在空间的概率分布，而不仅仅是点估计。
• 生成能力：VAE 不仅可以降维，还可以从潜在空间生成新数据。
• 连续性：VAE 的潜在空间通常更加连续和平滑，这在某些应用中可能更有用。
  注意事项
• 目的不同：虽然 VAE 可以用于降维，但其主要目的是学习数据的生成模型。如果仅需要降维，传统 AE 可能更直接。
• 解释性：VAE 的潜在空间可能不如 AE 那样直观，因为它包含概率信息。
• 计算复杂度：VAE 通常比简单的 AE 需要更多的计算资源。

总之，VAE 确实可以像 AE 一样用于降维和获取编码器向量，但它提供了更丰富的概率解释和生成能力。选择使用 VAE 还是 AE 取决于具体的应用需求和目标。