系列文章目录

Leetcode刷题:热题HOT100-EASY篇-Python多算法实现（完结-共21题）
Leetcode刷题:热题HOT100-Medium篇-Python多算法实现（完结-1~10题）
Leetcode刷题:热题HOT100-Medium篇-Python多算法实现（完结-11~20题）

前言

记录LeetCode 热题 HOT 100的Medium题目题解，采用python实现。

1.三数之和（双指针）*

1.1 题目描述

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

1.2 核心思路

参考了Leetcode题解思路：排序+双指针

1.3 代码

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        if len(nums)<3:return []
        nums.sort()
        result=[]
        for i in range(len(nums)):
            if nums[i]>0:break
            if i>0 and nums[i]==nums[i-1]:continue
            L,R=i+1,len(nums)-1
            while L<R:
                if nums[i]+nums[L]+nums[R]==0:
                    if L>i+1 and nums[L]==nums[L-1]:
                        L,R=L+1,R-1
                        continue
                    result.append([nums[i],nums[L],nums[R]])
                    L,R=L+1,R-1
                elif nums[i]+nums[L]+nums[R]>0:
                    R-=1
                elif nums[i]+nums[L]+nums[R]<0:
                    L+=1
        return result

2.下一个排列（双指针）*

2.1 题目描述

题目地址：31.下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ，找出 nums 的下一个排列。

必须 原地 修改，只允许使用额外常数空间。

输入：nums = [1,2,3]
输出：[1,3,2]

2.2 核心思路

参考了官方题解。
其核心思路如下：
1、在nums数组中寻找左边较小的数left和右边较大的数right，将其进行交换。
2、对于交换后的nums数组，对于right之后的所有子数组中的元素，对其进行升序排序。【理由：交换了left和right后的nums数组已经实现比原nums数组大，为了前后nums的差距减小，对right元素之后的数组进行升序排序，实现减小更新后nums排列的作用】
【举例： [4,5,2,6,3,1]】

对于算法实现主要分为两个部分：查找较大数和较小数；升序排序。

• 查找较大数和较小数：首先设置start，end分别存储左边较小数和右边较大数下标。初始化start=end=len(nums)-1。分析左边较小数的特性可以得到，左边较小数nums[start]满足nums[start]<nums[start+1]。即在[start+1,n]的子数组为降序数组。分析右边较大的数可以得到，右边较大的数是自右向左遍历nums时，第一个满足nums[end]>nums[start]的数。

• 升序排序：已经查找到start和end下标，交换nums[start]和nums[end]元素，然后对nums[start+1:]的元素进行升序排序即可。

【若start和end无法找到满足要求的下标，那么说明nums为降序排序，不存在可以交换的两个数，最终返回的下一个排列为nums的升序排序】
升序排序：

2.3 代码

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        if len(nums)==1:return nums
        #查找左边的较小数和右边的较大数
        n=len(nums)
        end,start=n-1,n-1
        for i in range(1,n):
            if nums[n-i-1]<nums[n-i]:
                end=n-i-1
                break
        while start>end:
            if nums[start]>nums[end]:
                break
            start-=1
        #将较小数和较大数交换位置，然后将较大数后面的子数组升序排序
        if start!=end:
            nums[start],nums[end]=nums[end],nums[start]
            nums[end+1:]=sorted(nums[end+1:])
        else:#nums为降序排序，无下一个排列
            nums=nums.reverse()
        return nums

3.搜索旋转排序数组（二分法）*

3.1 题目描述

题目链接：33.搜索旋转排序数组
整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

3.2 核心思路

由于时间复杂度为O(log n) ，很容易想到采用二分法。
初始化：low=0,high=len(nums)-1
二分循环：mid=(low+high)/2

• 若nums[mid]==target，则返回mid
• 若nums[mid]>nums[low]，在[low,mid]之间没有旋转排序，为升序数组。如果target处于[nums[low],num[mid]）中，那么high=mid-1；反之low=mid+1
• 若nums[mid]>nums[low]，则在[low,mid]之间存在旋转排序，[mid+1,high]之间为升序数组。如果target处于(nums[mid],num[high]]中，那么low=mid+1；反之high=mid-1

3.3 代码

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if len(nums)==1:return 0 if nums[0]==target else -1
        n=len(nums)
        low,high=0,n-1
        while low<=high:
            mid=int((low+high)/2)
            if nums[mid]==target:
                return mid
            #[0,mid]间无旋转
            if nums[0]<=nums[mid]:
                #若target在[low,mid]之间
                if target>=nums[low] and target<nums[mid]:
                    high=mid-1
                else:
                    low=mid+1
            #[0,mid]间旋转
            else:
                if target>nums[mid] and target<=nums[high]:
                    low=mid+1
                else:
                    high=mid-1
        return -1

4.在排序数组中查找元素的第一个和最后一个位置（二分法）*

4.1 题目描述

题目地址：在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

4.2 核心思路

通过二分法实现。核心思想为：查找第一个target的下标以及第一个大于target的数的下标。
【查找第一个target的下标】
采用正常的二分法，当nums[mid]==target 并且 nums[mid-1]<target时，返回mid
【查找第一个大于target的下标】
在正常二分法模板上进行改进，当num[mid-1]==target 并且 nums[mid]>target时，返回mid

4.3 代码

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        #寻找第一个大于等于target的下标；寻找第一个大于target的下标
        def searchNum(nums,target,flag):#flag=True表示查找大于等于target下标
            low,high=0,len(nums)-1
            while low<=high:
                mid=(low+high)//2
                if (nums[mid]==target) and flag:
                    if mid==0 or nums[mid-1]<target :return mid
                    high=mid-1
                elif nums[mid]>target:
                    if mid>=1 and nums[mid-1]==target and not flag:return mid
                    high=mid-1
                else:low=mid+1
            return -1 if flag else high+1
        if len(nums)==0:return [-1,-1]
        leftNum,rightNum=searchNum(nums,target,True),searchNum(nums,target,False)
        if leftNum==-1 or rightNum==-1:return [-1,-1]
        return [leftNum,rightNum-1]

5.旋转图像（矩阵，数组）

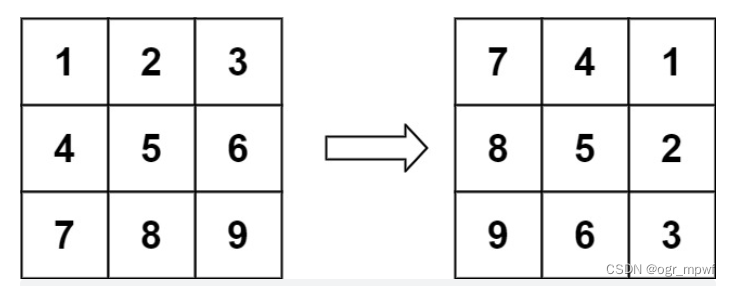
5.1 题目描述

5.2 核心思路

对于此题，将矩阵的旋转主要分为两个部分：

1. 对于matrix[i][j]来说，在经过90°顺时针旋转后，他将移动到哪个位置？
2. 对于原地旋转矩阵来说，以哪个顺序遍历矩阵中的元素，才能保证被覆盖的元素在之后还可以继续被找到？

【旋转位置公式】
通过观察可以发现，对于以下的矩阵来说，n=3

(0,0)->(0,2)
(0,1)->(1,2)
(0,2)->(2,2)

(1,0)->(0,1)
(1,1)->(1,1)
(1,2)->(2,1)

(2,0)->(0,0)
(2,1)->(1,0)
(2,2)->(2,0)

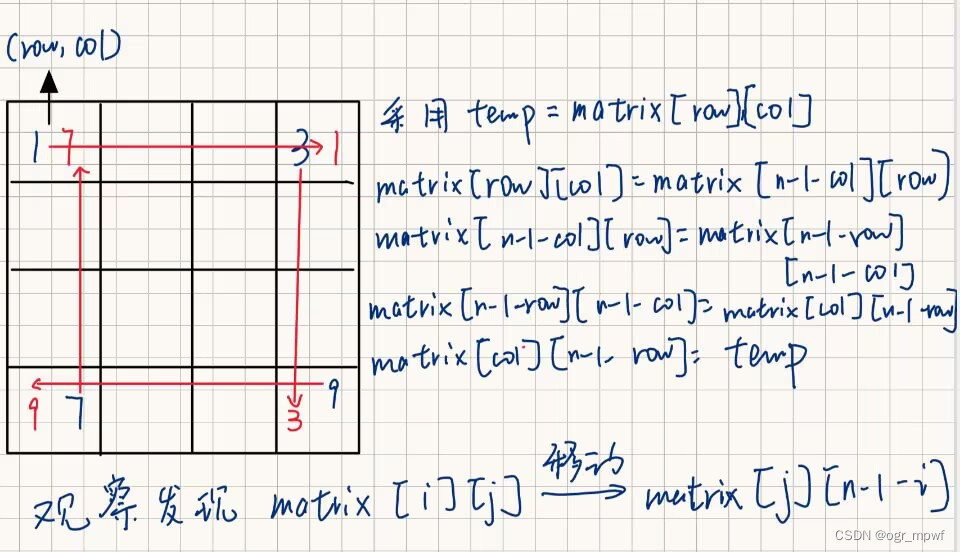
通过观察规律，可以得到matrix[i][j]将移动到matrix[j][n-1-i]

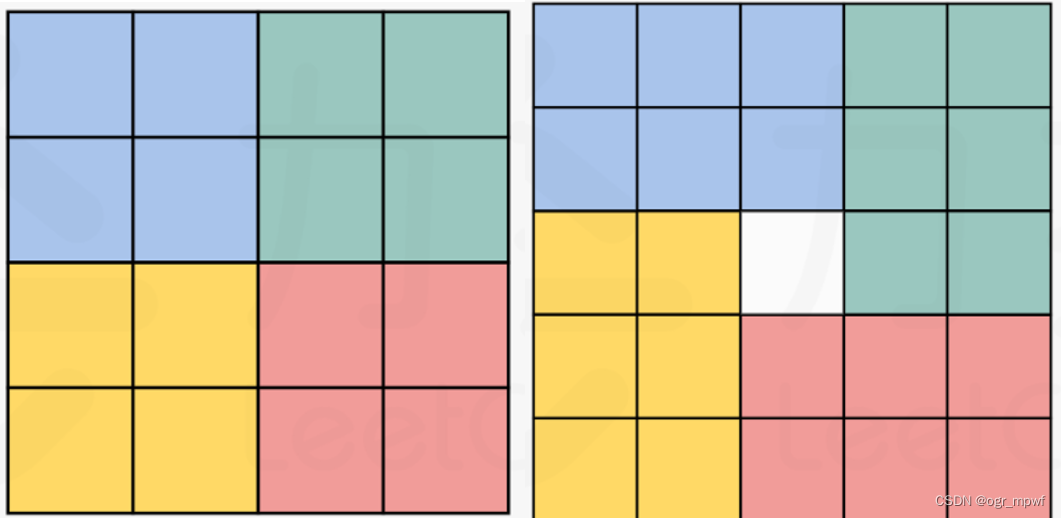
记录被覆盖元素的值到temp中，然后依次循环覆盖，可以得到上图。可以看出，顺时针旋转90°时4个元素一组循环覆盖，因此只需要temp记录其中一个元素，就可以实现原地旋转。

【遍历矩阵顺序】
如果初始元素为蓝色区域的元素，那么只需要将蓝色区域的元素全部移动到绿色区域，然后绿色区域移动到红色区域，红色区域移动到黄色区域，这样便可以得到最终结果。（图来自官方题解）。分为两种情况：

• 当n为偶数时，中间不存在需要移动的元素，此时遍历的块的长度和宽度为n/2
• 当n为奇数时，中间存在需要移动的元素，此时遍历的块的长度和宽度为n//2+1，n//2

可以得到height=n//2+n%2;width=n//2

5.3 代码

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n=len(matrix)
        blockL,blockW=n//2+n%2,n//2
        for i in range(blockL):
            for j in range(blockW):
                temp=matrix[i][j]
                matrix[i][j]=matrix[n-1-j][i]
                matrix[n-1-j][i]=matrix[n-1-i][n-1-j]
                matrix[n-1-i][n-1-j]=matrix[j][n-1-i]
                matrix[j][n-1-i]=temp

6.字母异位词分组（哈希表）

6.1 题目描述

题目地址：字母异位词分组
给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的字母得到的一个新单词，所有源单词中的字母通常恰好只用一次。

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

6.2 核心思路

通过哈希表存储相同字母组成的单词列表。对于strs中的每一个单词，首先将其按照字典序排序。

• 若排序后的单词不在哈希表中，则将排序后的单词作为key加入哈希表，value为列表，在列表中加入未排序的单词即可
• 若排序后的单词在哈希表中，只需要将哈希表中的value列表中增加未排序的单词即可。
  哈希表示例如下：
  

6.3 代码

class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        hashmap={}
        for word in strs:
            sortedWord="".join(sorted(word))
            if sortedWord not in hashmap:
                hashmap[sortedWord]=[word]
            else:
                hashmap[sortedWord].append(word)
        result=[]
        for key,value in hashmap.items():
            result.append(value)
        return result

7.最大子数组和（动态规划）

7.1 题目描述

题目地址：最大子数组和
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

7.2 核心思路

采用动态规划的思想，若通过dp[i]表示以nums[i]结尾的最大连续子数组和，那么可以得到:

dp[i]=max(dp[i-1]+nums[i],nums[i])

由此可以得到，dp[i-1]<0时，dp[i-1]+nums[i]<nums[i]，因此：

• dp[i-1]<0时，dp[i-1]=nums[i]
• dp[i-1]>=0时，dp[i-1]=nums[i]+dp[i-1]

由于dp[i]仅和dp[i-1]以及nums[i]有关，因此为降低空间复杂度，可以将dp[i-1]，dp[i]简化为两个局部变量来进行计算。

7.3 代码

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n=len(nums)
        formerSum,LastSum,maxSum=nums[0],0,nums[0]
        for i in range(1,n):
            LastSum=nums[i] if formerSum<=0 else nums[i]+formerSum
            formerSum=LastSum
            maxSum=max(maxSum,LastSum)
        return maxSum

8.跳跃游戏（贪心）

8.1 题目描述

题目地址：跳跃游戏
给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

8.2 核心思路

采用贪心的思想，采用maxTrueIndex维护当前最远可到达的距离。

• 初始化：maxTrueIndex=0
• 迭代更新：若第i个元素可以到达，那么位于[i,i+nums[i]]之内的元素均可到达，此时为了优化运算的时间，我们设置maxTrueIndex更新当前可到达的最远距离。maxTrueIndex=max(maxTrueIndex，i+nums[i])，位于maxTrueIndex下标之前的元素均可以到达。
• 结果返回：若maxTrueIndex>=len(nums)-1，那么最后一个下标可以到达，返回True；反之返回False

8.3 代码

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        maxTrueIndex=0
        for i in range(len(nums)):
            if i<=maxTrueIndex:
                maxTrueIndex=max(maxTrueIndex,i+nums[i])
                if maxTrueIndex>=len(nums)-1:return True
        return False

9.合并区间（排序）

9.1 题目描述

题目连接：合并区间
以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

9.2 核心思路

设置merge存储最终结果，算法流程如下：

1. 对于intervals数组按照每个元素中第一个数字排序
2. 循环遍历intervals数组：若merge为空，或者intervals[i]于merge最后一个元素不重合，则将intervals[i]加入merge中；否则，合并intervals[i]和merge的最后一个元素。
3. 返回merge

9.3 代码

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        if len(intervals)==1:return intervals
        intervals.sort(key=(lambda x:x[0]))
        merge=[]
        for i in range(len(intervals)):
            if len(merge)==0 or merge[-1][1]<intervals[i][0]:
                merge.append(intervals[i])
            else:
                merge[-1]=[min(merge[-1][0],intervals[i][0]),max(merge[-1][1],intervals[i][1])]
        return merge

10.不同路径（动态规划）

10.1 题目描述

题目地址：不同路径
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

10.2 核心思路

采用动态规划的思想，设置dp[i][j]表示机器人从起点走到(i,j)时的路径总数。由于机器人总是向下或者向右行走，因此，dp[i][j]的路径数目等于机器人从起点到达(i-1,j)的路径总数【向下走一步到达（i,j）】加上从起点到达(i,j-1)的路径总数【向右走一步到达（i,j）】

dp[i][j]=dp[i-1][j]+dp[i][j-1]

10.3 代码

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp=[[1]*n]*m
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[m-1][n-1]