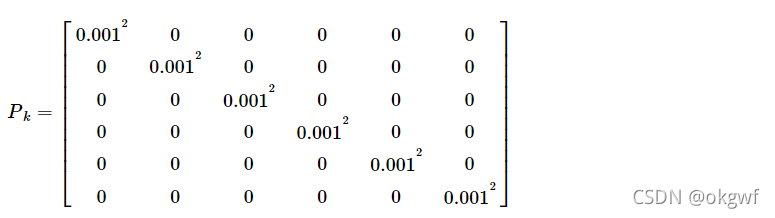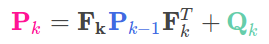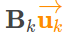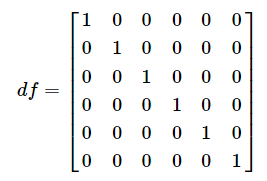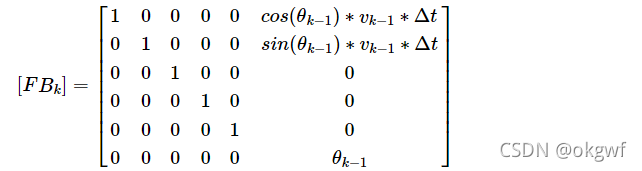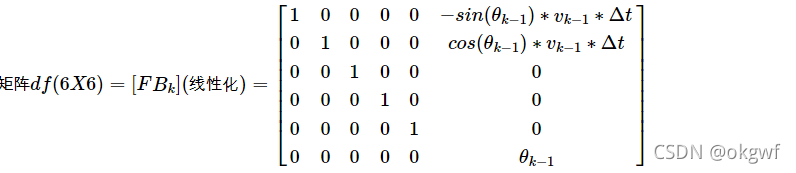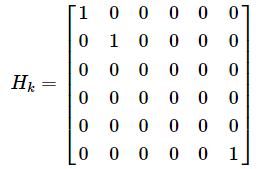本系列文章主要介绍如何在工程实践中使用卡尔曼滤波器,分七个小节介绍:
二.卡尔曼滤波器开发实践之二: 一个简单的位置估计卡尔曼滤波器
三.卡尔曼滤波器(EKF)开发实践之三: 基于三个传感器的海拔高度数据融合
四.卡尔曼滤波器(EKF)开发实践之四: ROS系统位姿估计包robot_pose_ekf详解 也就是本文
五.卡尔曼滤波器(EKF)开发实践之五: 编写自己的EKF替换robot_pose_ekf中EKF滤波器
六.卡尔曼滤波器(UKF)开发实践之六: 无损卡尔曼滤波器(UKF)进阶-白话讲解篇
七.卡尔曼滤波器(UKF)开发实践之七: 无损卡尔曼滤波器(UKF)进阶-实例篇
--------------------------------正文开始------------------------------------------
在我的工作学习中,只要涉及到智能汽车,智能机器人,经常会接触到基于多路传感器的位姿估计,比如ROS系统自带的,用于评估机器人的 3D 位姿的扩展卡尔曼滤波算法包: robot_pose_ekf.
这个包用于评估机器人的 3D 位姿，使用了来自不同源的位姿测量信息，它可以使用带有 6D（3D position and 3D orientation）模型信息的扩展卡尔曼滤波器来整合来自轮子里程计(odom)， 惯性传感器(IMU),视觉里程计(VO),以及GPS定位的数据信息。 根据ROS官方文介绍: robot_pose_ekf包采用松耦合方式融合不同传感器信息实现位姿估计。
下面我就从扩展卡尔曼滤波器(ekf)的五大公式角度,对robot_pose_ekf做详细分析.
分析重点我打算全部放在这个包EKF部分,对于这个包的基于ROS系统的入口代码,以及各种topic的订阅和发布,TF的监听和发布,已经从传感器收到位姿信息如何初处理,本文不做介绍.另外之这个包支持odom.imu,vo,gps四路传感器位姿信息融合,这里我只以常用的odom和imu两路位姿融合来介绍.
一. odom和imu传感器位姿信息输入
odom传感器数据格式: odom( x, y, z, roll,pitch,yaw): 其中,x,y作为智能车在平面地图的x和y坐标;z坐标忽略恒等于0; roll(车身纵向翻滚角)和pitch(车身俯仰角)也不做考虑恒等于0. yaw(偏航角)作为智能车在平面地图上左右转向方向角. 即: odom( x, y, 0, 0,0,yaw),共6个测量值数据. 此外odom传感器还提供自身的噪音协方差矩阵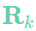
imu惯性传感器数据格式: imu(roll,pitch,yaw): 其中roll(车身纵向翻滚角)和pitch(车身俯仰角)也不做考虑恒等于0. yaw(偏航角)作为智能车在平面地图上左右转向方向角. 即: imu( 0,0,yaw),共3个测量值数据. 此外imu传感器还提供自身的噪音协方差矩阵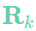
二. robot_pose_ekf位姿包系统状态列向量
系统状态列向量:X_k= ( x, y, z, roll,pitch,yaw), 实际有效值为: X_k= ( x, y, 0, 0,0,yaw). 理由同上odom.
三. robot_pose_ekf位姿包的核心: BFL::ExtendedKalmanFilter
先讲BFL(贝叶斯滤波器库),这是一个开源的贝叶斯滤波器库,里面包含有扩展的卡尔曼滤波器(ExtendedKalmanFilter). 根据robot_pose_ekf包据介绍,该包采用松耦合方式融合不同传感器信息实现位姿估计. 注意这个松耦合,这有别于前面文章中我介绍的高内聚的整体融合方式.
下面我就结合关键代码,介绍下robot_pose_ekf包是如何采用松耦合的方式使用BFL::ExtendedKalmanFilter的(详细robot_pose_ekf代码大家可以网上下载):
1. EKF初始化,及先验状态向量定义:
源码位置: odom_estimation.cpp
所在方法: OdomEstimation::initialize(const Transform& prior, const Time& time)
// set prior of filter
ColumnVector prior_Mu(6); //--->X_k-1 状态向量(6)先验(初始)估计值(x,y,z,roll,pitch,yaw)
decomposeTransform(prior, prior_Mu(1), prior_Mu(2), prior_Mu(3), prior_Mu(4), prior_Mu(5), prior_Mu(6));
SymmetricMatrix prior_Cov(6); //--->P_k-1 初始预测矩阵6x6,
for (unsigned int i=1; i<=6; i++) {
for (unsigned int j=1; j<=6; j++){
if (i==j) prior_Cov(i,j) = pow(0.001,2);
else prior_Cov(i,j) = 0;
}
}
prior_ = new Gaussian(prior_Mu,prior_Cov); //关于先验状态值的二维高斯分布
filter_ = new ExtendedKalmanFilter(prior_); //Construction of the Filter
// remember prior
addMeasurement(StampedTransform(prior, time, output_frame_, base_footprint_frame_));如代码和注释所示,这里定义:
- 先验状态列向量
: (x,y,z,roll,pitch,yaw), 即状态值个数: n = 6.
- 先验不确定性协方差矩阵
- 先验估计高斯函数: prior_ = new Gaussia(prior_Mu,prior_Cov), 注: 最后,ekf的最优估计值和最优协方差矩阵也将基于此高斯分布获取:
filter_->PostGet()->ExpectedValueGet();
filter_->PostGet()->CovarianceGet();
- 滤波器对象: filter_ = new ExtendedKalmanFilter(prior_);
- 最后,保存第一个odom位姿数据,等待imu数据到来,才开始数据融合.
Note: 整个过滤器的先验估计值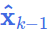
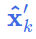
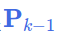
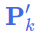
2. 松耦合的系统模式和传感器模型定义
源码位置: odom_estimation.cpp
所在方法: OdomEstimation::OdomEstimation()
<1> 系统预测模型
// create SYSTEM MODEL
ColumnVector sysNoise_Mu(6); sysNoise_Mu = 0;//预测模型状态向量X_k(6)
SymmetricMatrix sysNoise_Cov(6); sysNoise_Cov = 0;//预测噪音协方差矩阵Q_k(6x6)
for (unsigned int i=1; i<=6; i++) sysNoise_Cov(i,i) = pow(1000.0,2);
Gaussian system_Uncertainty(sysNoise_Mu/*均值:预测向量nx1*/, sysNoise_Cov/*预测噪音协方差矩阵nxn*/);//预测二维高斯分布
//非线性模型没有F_k,B_k. 但求得的雅各比矩阵, 相当于F_k和B_k的结合
sys_pdf_ = new NonLinearAnalyticConditionalGaussianOdo(system_Uncertainty/*指定预测模型高斯分布函数*/);//非线性概率密度函数
sys_model_ = new AnalyticSystemModelGaussianUncertainty(sys_pdf_);//整个系统的预测模型- 系统预测模型列向量
- 系统预测模型噪音协方差矩阵
:
- 系统模型非线性概率密度函数(PDF)和系统模型: sys_pdf_ 和 sys_model_
这一步sys_model_定义,其实对应EKF的公式<1>和公式<2>:
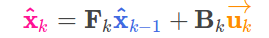
Note:
(1).现在只是定义了模型和必要的矩阵和向量, 真正的执行公式<1>和公式<2>,要等到针对sys_model_做更新(update)时才执行.
(2).本人也有个疑问:
上面的矩阵和向量定义是不是差点什么? 对,还不见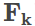
其实,预测矩阵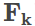
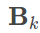
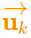
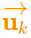
- 现在来看上面说的雅各比矩阵是如何定义
我们注意到这里的sys_pdf_ 的类名为: NonLinearAnalyticConditionalGaussianOdo.即这是一个非线性概率密度函数.
看到NonLinearAnalyticConditionalGaussianOdo类的定义,其有一个私有矩阵成员变量: MatrixWrapper::Matrix df;
再看NonLinearAnalyticConditionalGaussianOdo的实现代码:
NonLinearAnalyticConditionalGaussianOdo::NonLinearAnalyticConditionalGaussianOdo(const Gaussian& additiveNoise)
: AnalyticConditionalGaussianAdditiveNoise(additiveNoise,NUMCONDARGUMENTS_MOBILE),
df(6,6)
{
// initialize df matrix
//密度函数矩阵,雅各比矩阵F_k. 对参数1即状态向量X_k(3)求雅各比矩阵
for (unsigned int i=1; i<=6; i++){
for (unsigned int j=1; j<=6; j++){
if (i==j) df(i,j) = 1;
else df(i,j) = 0;
}
}
}
ColumnVector NonLinearAnalyticConditionalGaussianOdo::ExpectedValueGet() const
{
//条件概率密度的条件参数，状态与输入都是条件概率密度的私有变量。
ColumnVector state = ConditionalArgumentGet(0); //获取状态向量X_k(3)
ColumnVector vel = ConditionalArgumentGet(1); //获取输入向量z_k(2) ,这里是速度和方向
//进行非线性计算,更新状态
//近似执行 X_k = F_k * X_k-1 + B_k * u_k
//查看系统预测模型更新(update)时,控制向量输入都为方向为vel(1,2)均为0
state(1) += cos(state(6)/*theta*/) * vel(1)/*v*/; //根据速度v更新x轴位移
state(2) += sin(state(6)/*theta*/) * vel(1)/*v*/; //根据速度v更新y轴位移
state(6) += vel(2); //更新theta,即方向.
// Get the mean Value of the Additive Gaussian uncertainty,即:_additiveNoise_Mu: X_k-1(6)
return state + AdditiveNoiseMuGet();
}
Matrix NonLinearAnalyticConditionalGaussianOdo::dfGet(unsigned int i) const
{
if (i==0)//derivative to the first conditional argument (x) 状态向量X_k(6)
{
double vel_trans = ConditionalArgumentGet(1)(1);//输入向量的速度值
double yaw = ConditionalArgumentGet(0)(6);//状态向量的偏航角theta
df(1,3)=-vel_trans*sin(yaw); //求x关于yaw的偏导: x = vel(1)*cos(state(3)) x` = -vel(1)*sin(state(3))
df(2,3)= vel_trans*cos(yaw); //求y关于yaw的偏导 y = vel(1)*sin(state(3)) y` = vel(1)*cos(state(3))
return df;
}
else
{
/*...这里代码省略*/
}
}
上述代码完成以下工作:
(1). 构造函数中初始化矩阵df为:
(2).在ExpectedValueGet()方法中,完成了公式<1>
的完整计算. 具体怎么解释呢? 这里就要提到在本系列文章的第一节中介绍的非线性函数线性化问题.
根据初中物理运动学公式: St = S0 + v * t 得系统运动学方程:
x轴方向新位置x: x_k = x_k-1 + 0 + 0 + 0 + 0 + cos(θ) * v_k-1 * Δt
y轴方向新位置y: y_k = 0 + y_k-1 + 0 + 0 + 0 + sin(θ) * v_k-1 * Δt
直线运动速度v: θ_k = 0 + 0 + 0 + 0 + 0 + θ_k-1
即:
大家注意我这里写的是[FB_k], 即这个矩阵是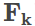
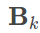
(注: 这里可以看出,系统控制向量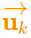
(3). dfGet(unsigned int i) 方法中有对上面动态生成的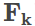
因为我们知道这上面运动方程明显是非线性的,且 cos(θ)和sin(θ) 明显是非线性曲线函数. 我们必须使用 cos(θ)和sin(θ)偏导函数来代替,由第一节的导函数定义引用知:
于是上面系统运动学方程线性化后为:
x轴方向新位置x: x_k = x_k-1 + 0 + 0 + 0 + 0 - sin(θ) * v_k-1 * Δt
y轴方向新位置y: y_k = 0 + y_k-1 + 0 + 0 + 0 + cos(θ) * v_k-1 * Δt
直线运动速度v: θ_k = 0 + 0 + 0 + 0 + 0 + θ_k-1
得:
注: robot_pose_ekf的dfGet(unsigned int i)方式实现其实有个错误:
df(1,3) = -vel_trans*sin(yaw);
df(2,3) = vel_trans*cos(yaw);
代码中df(1,3)应为df(1,6), df(2,3)应为df(2,6). 之所以错误的代码还能正常工作. 是因为robot_pose_ekf工作时,系统控制例向量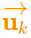
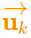
<2>. 测量值模型: odom测量模型和imu测量模型, (当然还有vo模型和gps模型, 略)
odom测量模型源码:
/*********************************
* Initialise measurement(update) model *
********************************/
// create MEASUREMENT MODEL ODOM
ColumnVector measNoiseOdom_Mu(6); measNoiseOdom_Mu = 0;//--->z_k(6) 6个测量值(x,y,z,roll,pitch,yaw)
SymmetricMatrix measNoiseOdom_Cov(6); measNoiseOdom_Cov = 0; //--->R_k 传感器噪音协方差矩阵6x6
for (unsigned int i=1; i<=6; i++) measNoiseOdom_Cov(i,i) = 1;
Gaussian measurement_Uncertainty_Odom(measNoiseOdom_Mu, measNoiseOdom_Cov);//关于测量值的二维高斯分布
//状态向量向测量值向量的转换矩阵(针对非线性为雅各比矩阵)mxn. m:测量值个数6, n:状态值个数6
Matrix Hodom(6,6); Hodom = 0;
Hodom(1,1) = 1; Hodom(2,2) = 1; Hodom(6,6) = 1;
odom_meas_pdf_ = new LinearAnalyticConditionalGaussian(Hodom/*状态值转测量值雅各比矩阵6x6*/, measurement_Uncertainty_Odom);
odom_meas_model_ = new LinearAnalyticMeasurementModelGaussianUncertainty(odom_meas_pdf_);
上述代码主要定义针对odom测量值的H_k, R_k, z_k:
- 定义odom测量值列向量
- 定义odom传感器噪音协方差矩阵
: measNoiseOdom_Cov; 并初始化对角线为1; 注: 后续此odom噪音协方差会用从odom传感器odom测量值一起而来odom噪音协方差矩阵替换.
- 定义状态值转测量值(转同尺度,度量等)转换矩阵
: Hodom(6x6), 因为都是线性恒等关系,得:
- 定义odom测量模型概率密度函数(PDF): odom_meas_pdf_ 和 odom_meas_model_
imu测量模型源码:
ColumnVector measNoiseImu_Mu(3); measNoiseImu_Mu = 0; //--->z_k(3) 3个测量值(roll,pitch,yaw)
SymmetricMatrix measNoiseImu_Cov(3); measNoiseImu_Cov = 0;//--->R_k 传感器噪音协方差矩阵3x3
for (unsigned int i=1; i<=3; i++) measNoiseImu_Cov(i,i) = 1;
Gaussian measurement_Uncertainty_Imu(measNoiseImu_Mu, measNoiseImu_Cov);//关于测量值的二维高斯分布
Matrix Himu(3,6); Himu = 0;//状态向量向测量值向量的转换矩阵(针对非线性为雅各比矩阵)mxn. m:测量值个数3, n:状态值个数6
Himu(1,4) = 1; Himu(2,5) = 1; Himu(3,6) = 1;
imu_meas_pdf_ = new LinearAnalyticConditionalGaussian(Himu/*状态值转测量值雅各比矩阵3x6*/, measurement_Uncertainty_Imu);
imu_meas_model_ = new LinearAnalyticMeasurementModelGaussianUncertainty(imu_meas_pdf_);
上述代码主要定义针对imu测量值的H_k, R_k, z_k:
- 定义imu测量值列向量
- 定义imu传感器噪音协方差矩阵
: measNoiseImu_Cov; 并初始化对角线为1; 注: 后续此imu噪音协方差会用从imu传感器imu测量值一起而来imu噪音协方差矩阵替换.
- 定义状态值转测量值(转同尺度,度量等)转换矩阵
- 定义imu测量模型概率密度函数(PDF): imu_meas_pdf_ 和 imu_meas_model_
此外, robot_pose_ekf包还支持vo(视觉odom),gps. 只是配置它们不启用. Vo和odom的代码实现和odom和imu十分类似,此处不在阐述.
3. ExtendedKalmanFilter实例更新过程(update()):
源码位置: odom_estimation.cpp
所在方法: OdomEstimation:: update (……)
<1>系统预测模型: sys_model_.update()
// system update filter
ColumnVector vel_desi(2); vel_desi = 0;
filter_->Update(sys_model_, vel_desi/*控制向量:u_k*/); //分步更新系统预测模型
以上代码:
- 定义系统预测模型的控制向量u_k(v, θ),两个元素v和θ恒等以0. 这里也就解释了为什么前面sys_model_定义时,提供的FB_k联合矩阵有问题,但仍影响运行结果了.
- 使用sys_model_以vel_desi为控制向量
执行卡尔曼滤波器公式(1):
和公式(2)
.
其中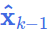
使用 EKF初始化时的 prior_Mu(6)(首次执行)或
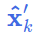(上次执行的最优估计值);
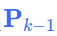使用 EKF初始化时的 prior_Cov(6) (首次执行)或
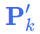(上次执行的最优协方差矩阵);
- sys_model_更新完,结果:
和
保存到ExtendedKalmanFilter实例filter_中.
<2>测量模型更新: odom模型odom_meas_model_和imu模型imu_meas_model_. 其他vo_meas_model_和gps_meas_model_类似不在阐述.
odom测量模型源码:
// update filter
odom_meas_pdf_->AdditiveNoiseSigmaSet(odom_covariance_ * pow(dt,2));//更新odom协方差,即更新前面measNoiseOdom_Cov
filter_->Update(odom_meas_model_, odom_rel/*测量向量:z_k*/); //分步更新odom测量模型
以上odom更新代码:
- 把随同odom传感器测量值一起的odom传感器噪音协方差矩阵乘以pow(dt,2)后,设置到初始化阶段定义的odom概率密度函数odom_meas_pdf_, 即动态更新了odom的
.
- 使用odom_meas_model_以odom_rel为测量值列向量
和公式(5)
.
- 从ExtendedKalmanFilter实例filter_中取出
和
,参与公式(4)和公式(5)计算后,把最终结果:后验估计值(或最优估计值)保存到实例filter_的
;
imu测量模型源码: 大致和odom过程一样, 略.
<3> 准备下次更新(update)准备工作, 包含系统预测模型更新和测量值模型更行
把后验估计值(或最优估计值) 
把后验协方差矩阵(或最优协方差矩阵) 
<4> 获取最优估计
主程序通过调用ExtendedKalmanFilter实例filter_->PostGet()->ExpectedValueGet();获取当前最优估计,作为输出发布给其他程序使用.
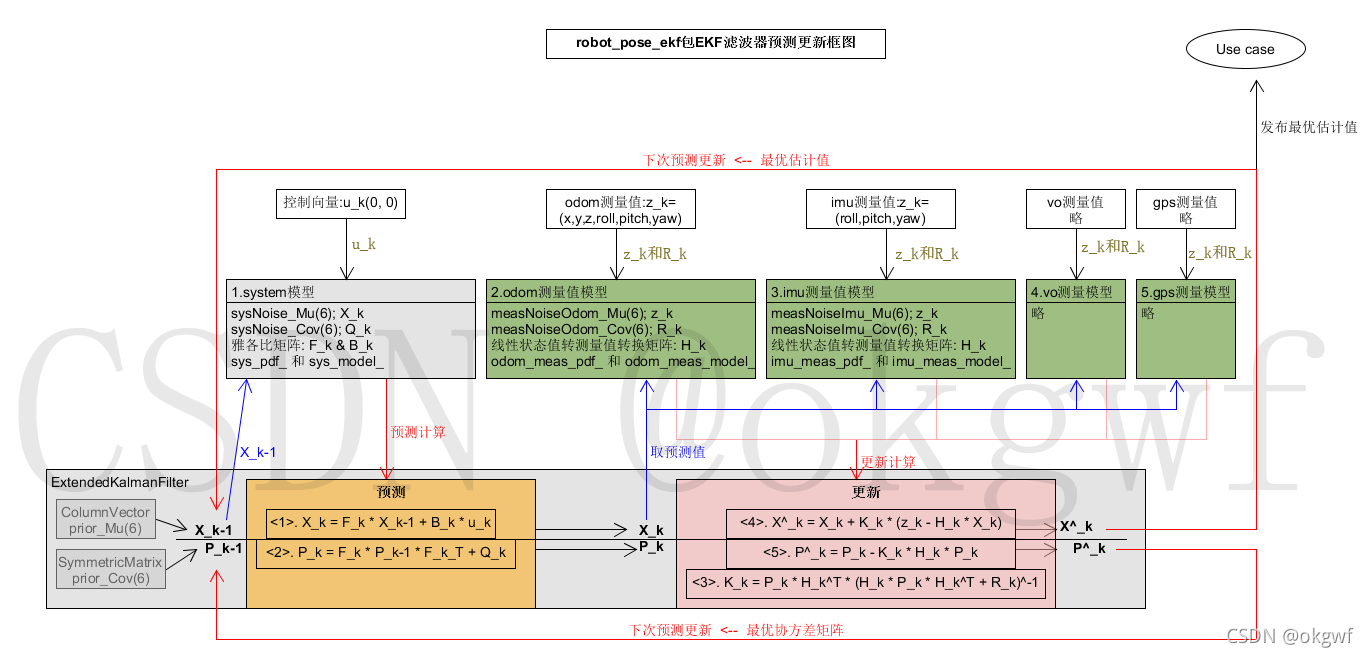
4. robot_pose_ekf功能包中EKF整体的预测/更新架构图:
最后,发张本人制作的robot_pose_ekf中ekf代码架构图. 直观地看看何为"松耦合方式融合".
