因子分析（factor analysis）过程

因子分析是一种常用的特征提取方法，可以被认为是主成分分析（Principal Component Analysis, PCA）的扩展。因子分析与PCA最大的区别在于，因子分析得到的隐藏因子具有可解释性，具有较高的实用价值。现如今，对于因子分析在提高模型可解释性和有效性的研究还尚未得到彻底的分析和探索。

因子分析通过对相关矩阵的分析，寻找一些支配特征间相关性的独立的潜在因子，简化观测数据，从而挖掘有效信息。为了获得具有代表性的隐藏因子，只有当样本充足且变量之间具有较强的相关性时，因子分析的结果才有效。因此，在因子分析之前，通常需要采用Kaiser-Meyer-Olkin（KMO）检验和巴特利特检验来判断数据是否适合使用因子分析挖掘共性因子。

KMO检验基于皮尔逊相关系数和偏相关系数之间的关系。对于所有特征，当皮尔逊相关系数的平方和远远大于偏相关系数的平方和时，说明观测数据的样本量充足，特征之间存在共性因子。

假设预处理后的数值为数据[D, Y],是监测特征的矩阵，是因变量。如前文所述，对于包含N个特征和K个样本的，(Di = [xi1, xi2, ..., xik], i = 1, 2, ..., N)，变量Di和Dj的皮尔逊相关系数记为rij(i, j =1, 2, ..., N)，控制剩余变量的偏相关系数记为pij。则KMO检验的检验统计量M为：

(1)

其中，R和Q分别是所有特征皮尔逊相关系数和偏相关系数的平方和。一般情况下，当M（也被称为KMO值）大于0.5时，数据适合进行因子分析。

巴特利特检验的原假设是“特征的相关系数矩阵C是单位矩阵”，其检验统计量Φ是相关系数矩阵C的行列式。

(2)

矩阵C中第i行j列元素rij是变量Di和Dj的皮尔逊相关系数(i, j =1, 2, ..., N)。

根据自由度和统计值，通过查询卡方分布表，可以近似地得到巴特利特检验的伴生概率。根据伴生概率p与显著性水平α之间的关系，可以确定特征D1, D2, ..., DN是否适合进行因子分析。当p<α时，应拒绝原假设，则相关矩阵C不是一个单位矩阵，特征之间存在明显的相关性。本论文的显著性水平设为0.05，这也是当前最常用的显著性水平。

对于，其因子分析模型的结果可以被描述为：

(3)

其中F是得到的相互独立的隐藏因子的矩阵(H ≤ N)，转化矩阵A被成为载荷矩阵，aij表示特征Di在因子Fj上的载荷，是均值为零、方差为有限值的随机误差项。

因子分析的目标是使相似（或相同类型）特征在每个因子上的载荷一致，即同时比较大或同时比较小。从而使得，单个因子对相似特征具有相同的意义表征。在这种情况下，就要求在不同的因子之间有明显的差异。为了得到这样的隐藏因子，我们需要在拟合公式(3)的基础上尽可能地降低因子之间的相关性。从同样是线性组合模型的PCA出发，研究者们设计了一个便捷、有效的因子分析过程，大大降低了因子分析模型优化的复杂度。这个方法基于对PCA得到的线性组合特征进行坐标旋转，以最大限度地提高这些线性组合特征之间的差距。得益于PCA的优点，这一过程还可以观测到隐藏因子对原始特征的信息提取程度。

因子分析的步骤如下所示：

计算（预处理后的）原始特征D1,D2, ...,DN的相关系数矩阵C，以及C的所有特征（）和相应的特征向量（）。当设置主成分个数为N时，基于PCA得到的线性组合特征被称为主成分。对于主成分(i =1, 2, ..., N)，其方差贡献率vcri和累积方差贡献率ccri分别为：

(4)

(5)

主成分分析中的主成分个数可以根据实际需求或数据特征来确定，这N个完整的主成分被认为是因子分析的基础因子。

(6)

2. 当设置隐藏因子的个数为H时，基础的载荷矩阵可以由相关系数矩阵C的前H个特征值和特征向量获得。

(7)

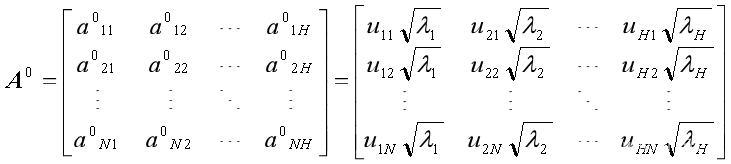
3. 需要进行坐标旋转，使相似（或相同类型）特征在各因子上的载荷大小保持一致，以提高因子的实际意义。Varimax准则是因子坐标旋转中最常用的方法，通过最大化所有因子的载荷的方差和，使所得到的因子之间的差异更加明显。具体而严，首先将原始特征按照相关性分组，使用Varimax准则进行坐标旋转，优化过程使同组特征的载荷相似（距离小），不同组特征的载荷差别明显（距离大）。从而确保相关性强的特征在同一因子上的载荷大小是一致的，且不同的因子对应不同的特征组组合。旋转后的载荷矩阵被记为矩阵A（此即为因子分析模型中的载荷矩阵）。

(8)

4. 使用回归估计法，可以计算得到因子得分系数矩阵G，以及各个因子。

(9)

(10)

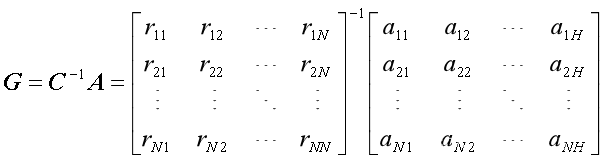
这里C-1是相关系数矩阵C的逆矩阵。则：

(11)

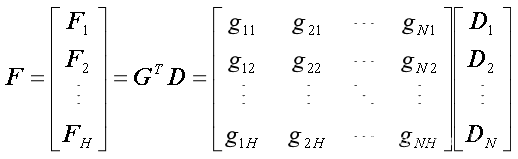
确定共性因子个数是上述因子分析过程中的关键步骤。通常，因子个数可以根据实际需求或特征相关性分析来决定。但对于复杂系统，由于复杂的功能和结构难以分析，且监测特征大多存在冗余，因此很难确定可能涵盖的隐藏因子个数。因此，在本论文中，我们设计了选取因子个数的依据：确保共性因素能够尽可能多地从监测特征中提取信息，且每个监测特征都能有代表其的因子以便于后续分析特征之间关系。并给出了设置因子个数和给因子命名的一般规则，如下所示：

1. 首先，根据初始因子（即主成分）的累积方差贡献率，可以得到累积方差贡献率达到80%以上时的最小因子数（最小主成分数），定义为H1。

2. 其次，令H ≥H1，计算所有特征的因子提取度，使每个特征的因子提取度超过70%的最小因子数就是最终确定的因子个数。这里，因子提取度表示原始特征能被因子解释的部分的方差在总体中的占比。当因子数为H时，特征Di（i =1,2,...,N）的因子提取度，记为，是载荷矩阵中第j列元素的平方和。

(12)

3. 上述阈值80%和70%是特征提取中常用的数值，实际上也可根据需要选择其他阈值，比如85%和75%的组合。此外，还可以根据实际数据的特征使用适当的阈值。例如，当因子个数持续增加，但累积方差贡献率或特征的因子提取度几乎没有增加时，则可以根据主观经验选择合适的因子个数。

4. 当特征Di在因子Fj上的载荷大于0.6时，我们称Fj是Di的代表因子，或Di是Fj的一个表示特征。这里，阈值0.6是根据之前设置的因子提取度阈值计算得到的，也可以直接使用。这意味着因子Di从原始特征Di中提取了一半以上的有效信息。

隐藏因子实际上代表了原始监测特征之间的关系。因此，在命名过程中，一个因子可以直接命名为其表示特征的组合。如果一个因子只有一个表示特征，则可以直接使用该特征的名称为该因子命名。当然，当因子的实际意义可以根据其代表特征之间的共性分析得到时，可以用因子的实际意义来命名。此外，如果存在一个特征的因子提取度大于70%，但其却没有代表性因子时，可以认为该特征是一个受多种潜在因素影响的综合性特征（即已经融合了不同信息的特征）。

粗略的Python代码：

import pandas as pd
import numpy as np
import numpy.linalg as nlg
from factor_analyzer import FactorAnalyzer, calculate_kmo, calculate_bartlett_sphericity
from sklearn import preprocessing

source_data = pd.read_csv('data.csv')
data = source_data.values
ss = preprocessing.StandardScaler()
array = ss.fit_transform(data)
print(array)
data = pd.DataFrame(list(array), columns=source_data.columns)
#print(data)
data_corr = data.corr()
#print("\n相关系数:\n",data_corr)

kmo = calculate_kmo(data)
bartlett = calculate_bartlett_sphericity(data)
print("\n因子分析适用性检验:")
print('kmo:{},bartlett:{}'.format(kmo[1], bartlett[1]))


fa = FactorAnalyzer(rotation=None, n_factors=38, method='principal')
fa.fit(data)
fa_sd = fa.get_factor_variance()
fa_df = pd.DataFrame(
    {'特征值': fa_sd[0], '方差贡献率': fa_sd[1], '方差累计贡献率': fa_sd[2]})

#各个因子的特征值以及方差贡献率
print("\n", fa_df)
factors = 19
#设置公因子个数，重新拟合
fa = FactorAnalyzer(rotation=None, n_factors=factors, method='principal')
fa.fit(data)

#查看公因子提取度
print("\n公因子提取度:\n", fa.get_communalities())

#查看因子载荷
print("\n因子载荷矩阵:\n", fa.loadings_)

#使用最大方差法旋转因子载荷矩阵
fa_rotate = FactorAnalyzer(rotation='varimax', n_factors=factors, method='principal')
fa_rotate.fit(data)

#查看旋转后的因子载荷
print("\n旋转后的因子载荷矩阵:\n", fa_rotate.loadings_)

# 因子得分（回归方法）（系数矩阵的逆乘以因子载荷矩阵）
X1 = np.mat(data_corr)
X1 = nlg.inv(X1)

factor_score = np.dot(X1, fa_rotate.loadings_)
factor_score = pd.DataFrame(factor_score)
factor_score.columns = ['F1', 'F2', 'F3', 'F4', 'F5', 'F6', 'F7', 'F8','F9', 'F10', 'F11','F12', 'F13', 'F14', 'F15', 'F16', 'F17', 'F18', 'F19']
factor_score.index = data_corr.columns
print("\n因子得分：\n",factor_score)

fa_t_score = np.dot(np.mat(data), np.mat(factor_score))
F_factors = pd.DataFrame(fa_t_score,columns=factor_score.columns)


def writedata(data):
    writer = pd.ExcelWriter("得分_19.xlsx", encoding="utf-8-sig")
    data.to_excel(writer, 'Sheet1')
    writer.save()
fa_zh = pd.DataFrame(fa_t_score) #factor_score.columns
writedata(factor_score)

因子分析可用于解耦复杂结构型数据的因果关系，得到的因子不仅互相独立且具有实际意义（可解释性），基于因子挖掘到的因果关系是稀疏、稳定、可验证的。

参考文章：https://onlinelibrary.wiley.com/doi/10.1111/exsy.13197

https://www.researchgate.net/publication/365665540_Fault_diagnosis_for_high-speed_train_braking_system_based_on_disentangled_causal_representation_learning

因子分析（factor analysis）过程

悦读