TEB算法原理与代码分析
详细文档+代码分析+matlab程序包
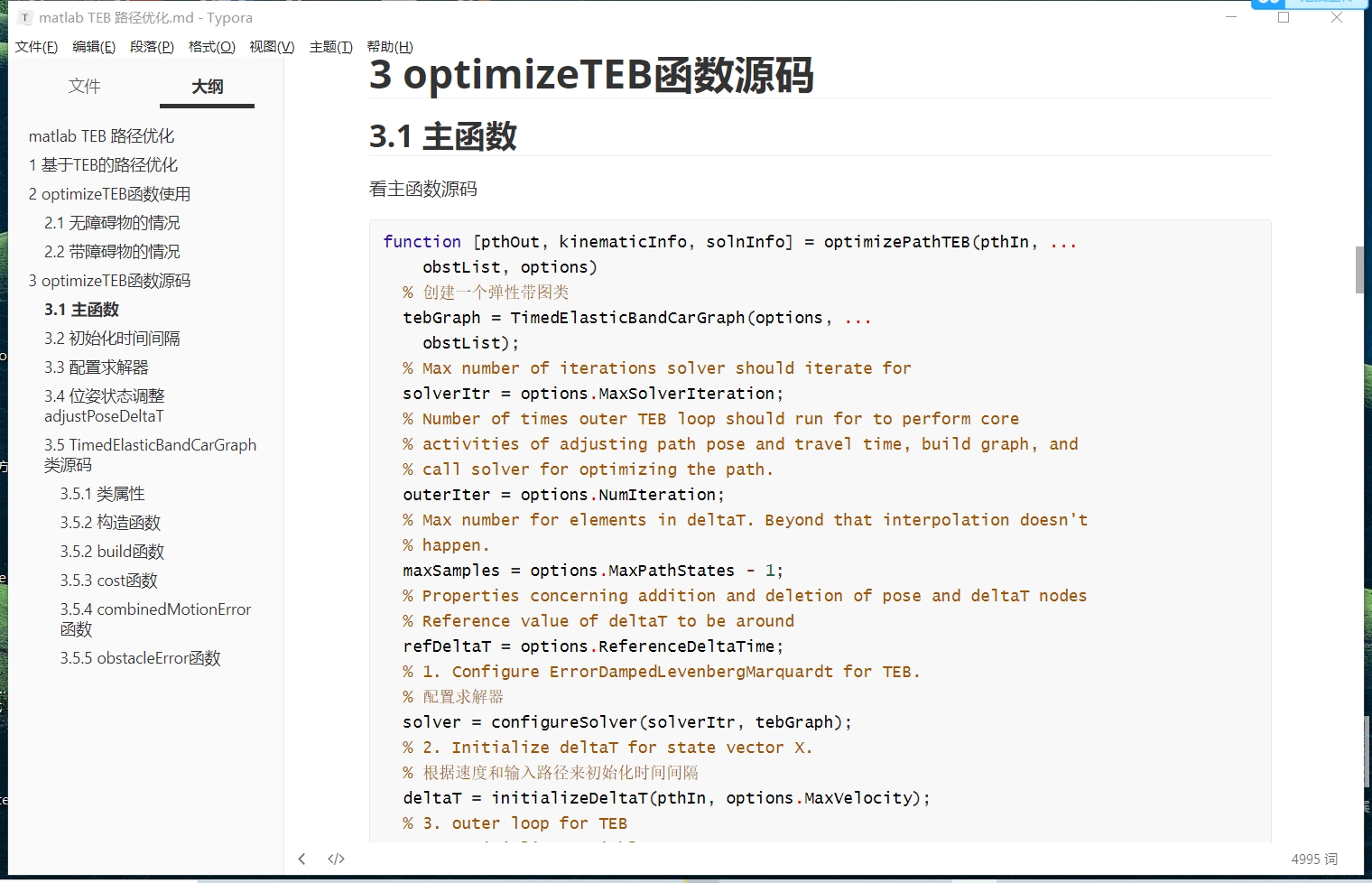
这段代码看起来是一个路径规划算法的实现。它使用了优化算法来寻找从起点到终点的最优路径,考虑了速度约束、运动学约束和障碍物避障。
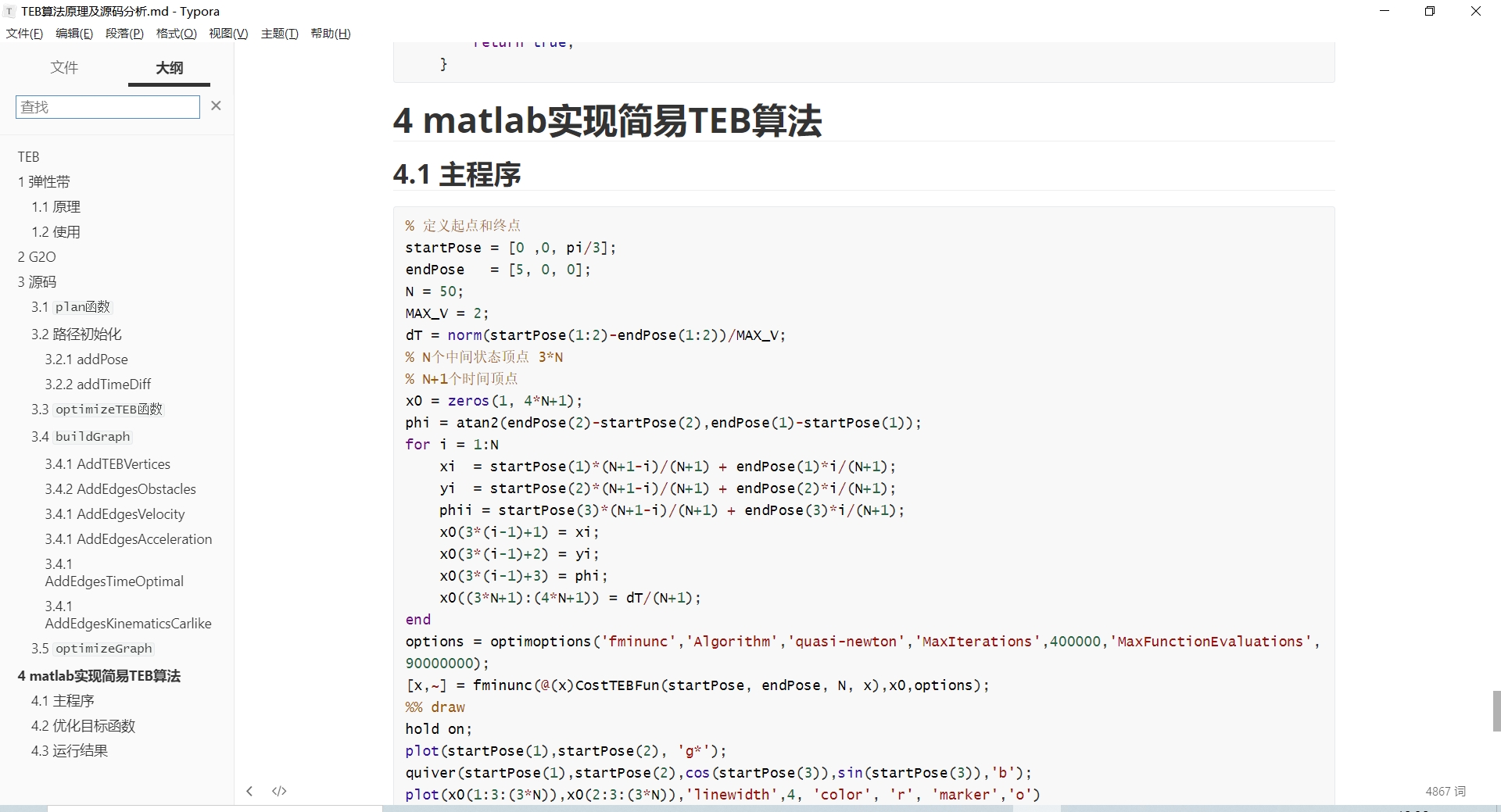
首先,代码定义了起点和终点的位置,以及障碍物的位置(如果有)。然后,它设置了一些参数,如路径中的中间状态顶点数量N、最大速度MAX_V和时间步长dT。
接下来,代码初始化了一个状态向量x0,用于存储路径规划的初始解。它根据起点和终点的位置,以及N的数量,计算了中间状态顶点的位置和朝向,并将它们存储在x0中。同时,它还计算了每个状态顶点之间的时间间隔dT,并将其存储在x0中。
然后,代码使用优化算法(fminunc函数)来最小化一个成本函数(CostTEBFun函数)。这个成本函数考虑了时间最小约束、速度约束、运动学约束和障碍物避障。优化算法将调整状态向量x0的值,以找到使成本函数最小化的最优解x。
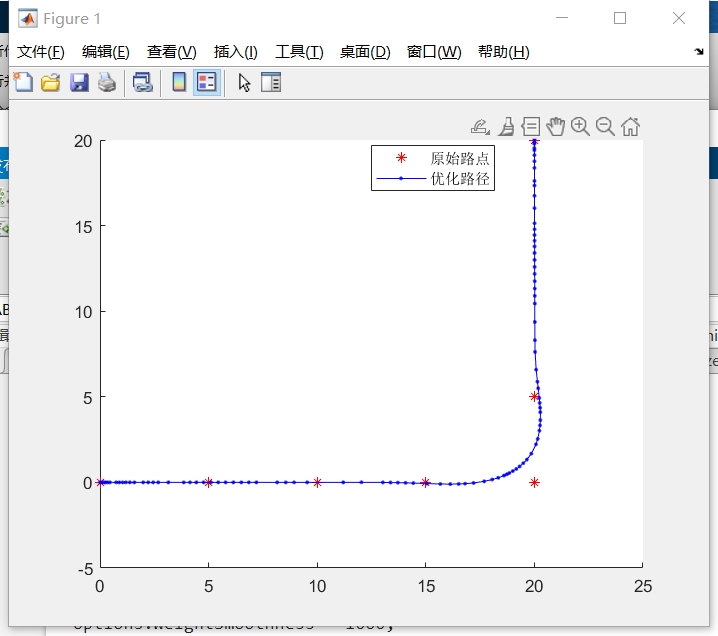
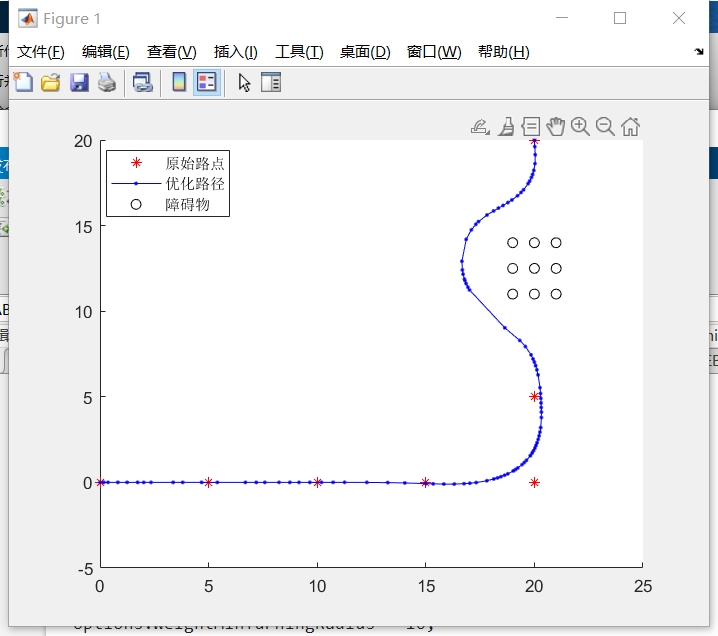
最后,代码绘制了路径规划的结果。它使用plot函数绘制了起点、中间状态顶点和终点的位置,使用quiver函数绘制了起点和中间状态顶点的朝向。如果有障碍物,它还使用plot函数绘制了障碍物的位置。
总结一下,这段代码实现了一个路径规划算法,用于寻找从起点到终点的最优路径。它考虑了速度约束、运动学约束和障碍物避障,并使用优化算法来搜索最优解。这个算法可以应用于机器人导航、自动驾驶等领域,解决路径规划问题。它涉及到的知识点包括优化算法、几何计算和路径规划算法。
YID:4179654252546507
autorobot
TEB算法原理与代码分析
TEB算法(Time-Elastic Band)是一种路径规划算法,旨在寻找从起点到终点的最优路径。它考虑了速度约束、运动学约束和障碍物避障,通过优化算法在时间上弹性的路径中搜索最优解。
首先,TEB算法的实现需要定义起点和终点的位置,以及可能存在的障碍物的位置。这些位置信息被用来确定路径规划的范围,并在后续的计算中起到重要作用。
接下来,算法设置了一些参数,以控制路径规划的细节。其中包括中间状态顶点的数量N,最大速度MAX_V和时间步长dT。这些参数的设置对于路径规划的效果有重要影响,需要根据具体应用场景进行调整。
然后,算法初始化了一个状态向量x0,用于存储
以上相关代码,程序地址:http://wekup.cn/654252546507.html