目录
一、什么是红黑树
红黑树是一种特殊的二叉搜索树,它在每个节点上增加了一个颜色属性,可以是红色或黑色。
1.1 红黑树的规则
- 每个节点要么是黑色要么是红色。
- 根节点是黑色。
- 每个叶子节点(NIL节点,空节点)是黑色。
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
- 如果⼀个结点是红⾊的,则它的两个孩⼦结点必须是黑色的,也就是说任意⼀条路径不会有连续的红⾊结点。
enum colour
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
colour _col;
//三叉链
RBTreeNode(const pair<K, V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
{}
};1.2 红黑树的特性
假设从根节点开始到NULL节点最短的路径高度为bh,则红黑树的总高度h满足:bh <= h <= 2*bh。
二、红黑树的插入
2.0 插入思路
总体思路:
- 先按照搜索二叉树的规则进行插入,然后通过一系列操作使之满足红黑树的规则。
- 如果是空树插入,新增结点是黑色结点。如果是非空树插⼊,新增结点必须红色结点。
if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK; return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { if (cur->_kv.first > kv.first) { parent = cur; cur = cur->_left; } else if (cur->_kv.first < kv.first) { parent = cur; cur = cur->_right; } else { return false; } } cur = new Node(kv); cur->_col = RED; if (parent->_kv.first < kv.first) { parent->_right = cur; } else { parent->_left = cur; } //链接父亲 cur->_parent = parent;- 插入后,如果其父亲节点是黑色的,则满足红黑树的规则。如果父亲节点是红色的,则不满足(红色节点的子节点都为黑色)的规则,需要调整。
2.1 情况一
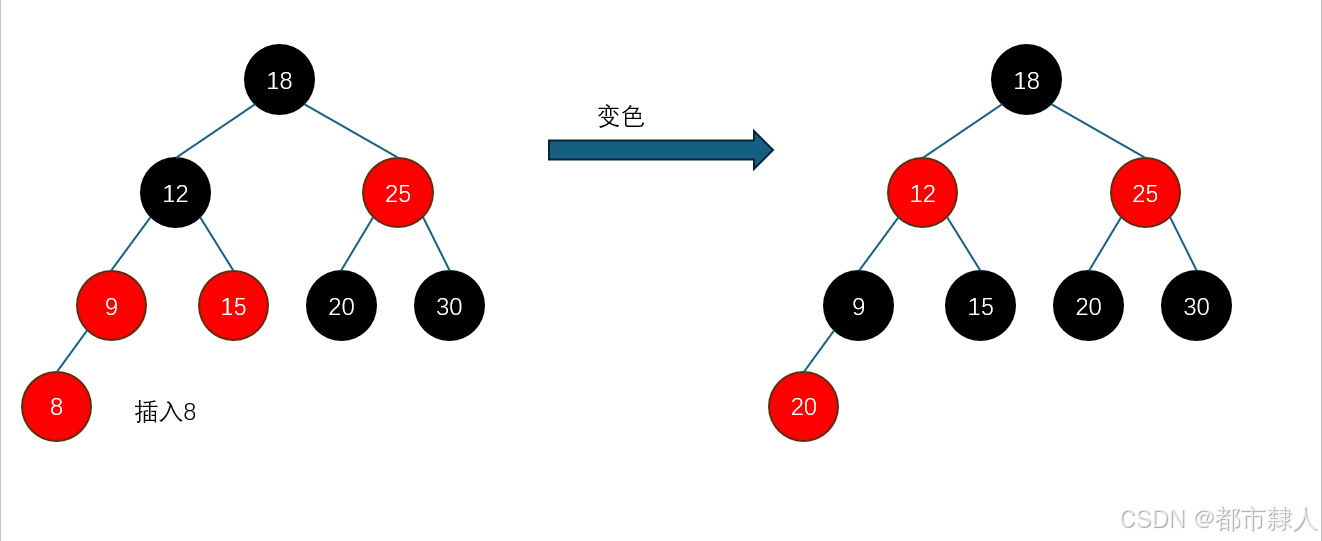
叔叔节点存在且为红色
- 考虑一般情况:
让“叔叔”节点变为黑色,“爷爷”节点变为红色 ,“父亲”节点变为黑色- 考虑特殊情况:
插入的树可能只是其中的一颗子树,爷爷节点的颜色变化可能会违反规则
所以,将cur指向爷爷节点,继续进行处理
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续往上处理
cur = grandfather;
parent = cur->_parent;
}2.2 情况二
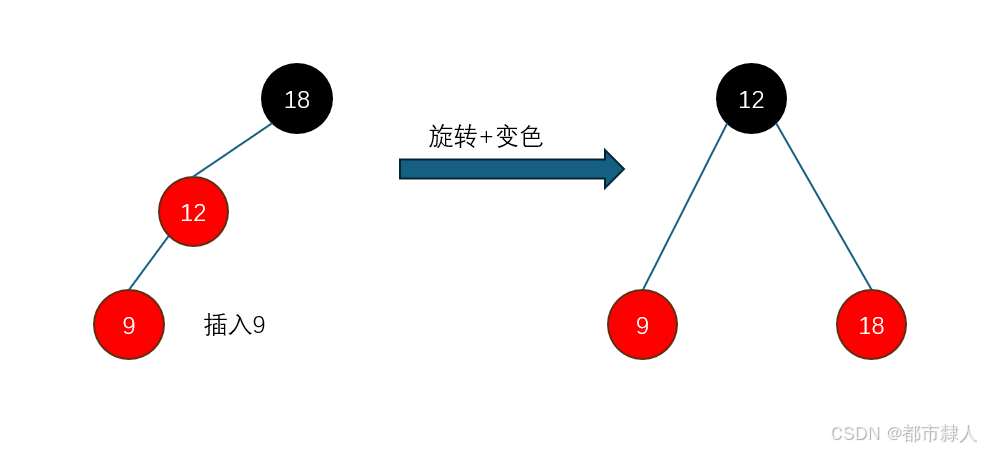
- 叔叔节点不存在
cur指向的一定是新增的节点- 叔叔节点存在但是为黑色
cur指向的一定不是新增的节点,而是某个子树新增了节点导致其爷爷节点变成了红色
如果父亲在爷爷的左边:则右旋
如果父亲在爷爷的右边:则左旋
最后:父亲节点变黑,爷爷节点变红
//父亲在爷爷的左树
if (cur == parent->_left)
{
RotateR(grandfather);
//变色
parent->_col = BLACK;
grandfather->_col = RED;
}
//父亲在爷爷的右树
if (cur == parent->_right)
{
RotateL(grandfather);
//变色
parent->_col = BLACK;
grandfather->_col = RED;
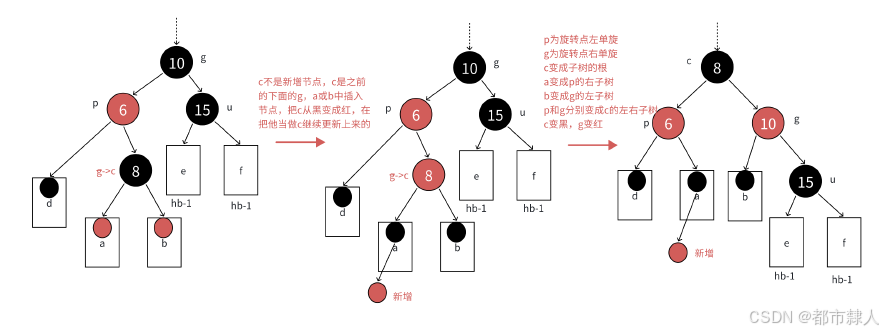
}2.3 情况三
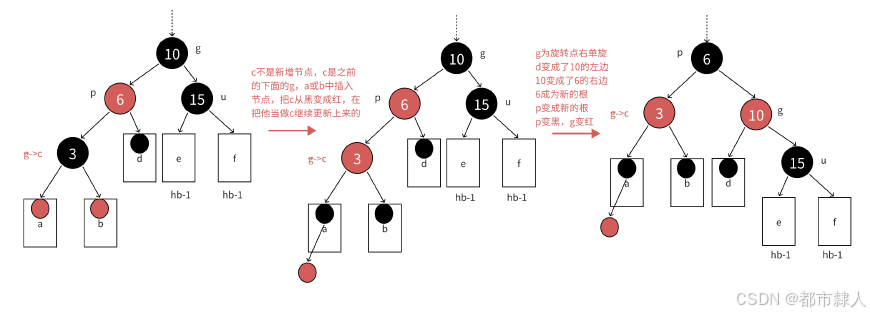
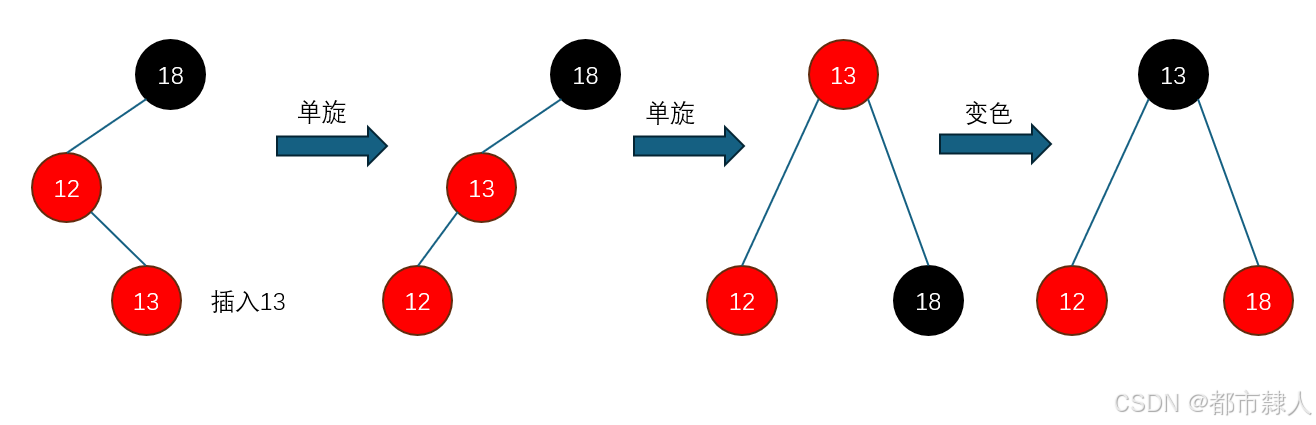
- 叔叔节点不存在
cur指向的一定是新插入的节点- 叔叔节点存在但是为黑色
cur指向的一定不是新增的节点,而是某个子树新增了节点导致其爷爷节点变成了红色
//父亲节点在爷爷节点的左边
RotateL(parent);
RotateR(grandfather);
//变色
cur->_col = BLACK;
grandfather->_col = RED;
//父亲节点在爷爷节点的右边
RotateR(parent);
RotateL(grandfather);
//变色
cur->_col = BLACK;
grandfather->_col = RED;2.2 插入代码
旋转部分代码详见:数据结构之AVL树(万字详解)_avl树 详解-CSDN博客
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//链接父亲
cur->_parent = parent;
//父亲是红色、处理
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (grandfather->_left==parent)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
RotateR(grandfather);
//变色
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateL(parent);
RotateR(grandfather);
//变色
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
RotateL(grandfather);
//变色
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateR(parent);
RotateL(grandfather);
//变色
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}