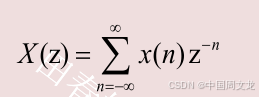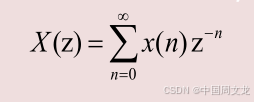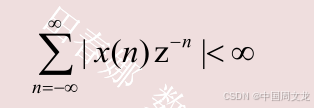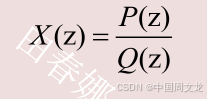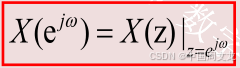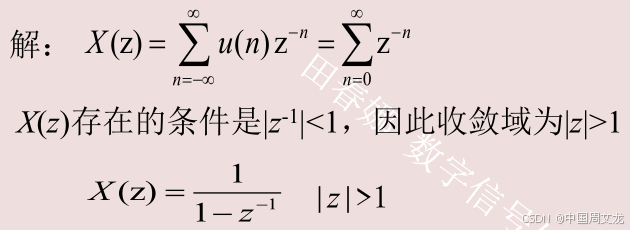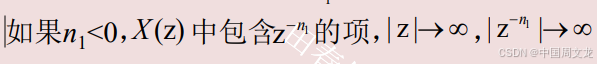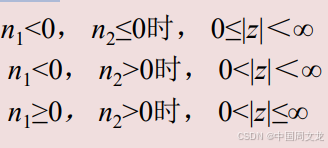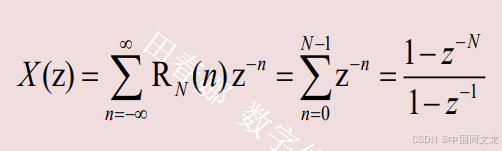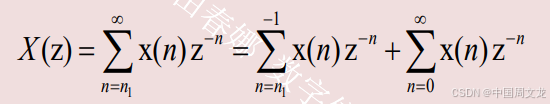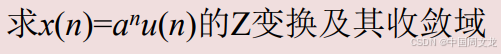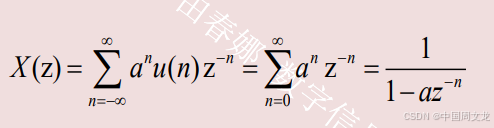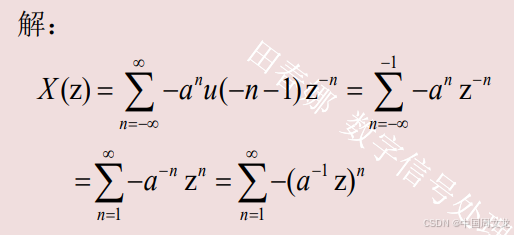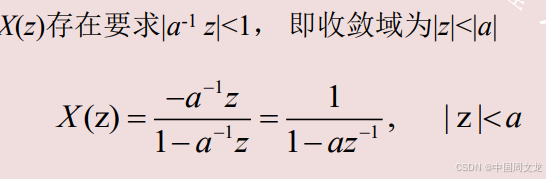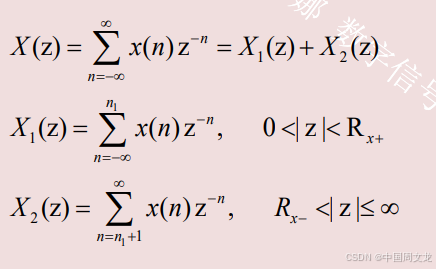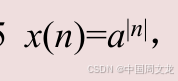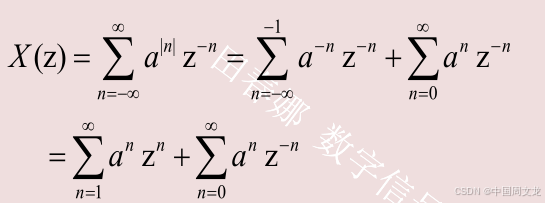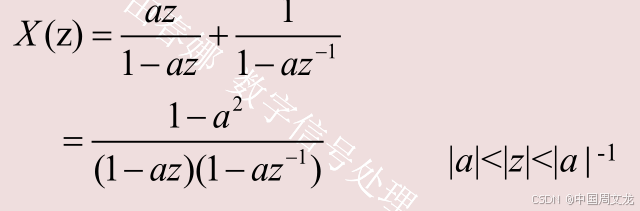关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络,如有侵权请联系编者
目录
3.2.1 离散时间信号的Z变换的定义
序列x(n)的Z变换定义为
z是一个复变量,它所在的复平面称为z平面。注意在定义中,对n求和是在±∞之间求和,称为双边Z变换。单边Z变换的定义如下
对于因果序列,用两种Z变换定义计算出的结果是一样的。本课程如不特别声明,均用双边Z变换对信号进行分析和变换
Z变换存在的条件是 (3.2.1) 式等号右边级数收敛 ,要求级数 绝对可和,即
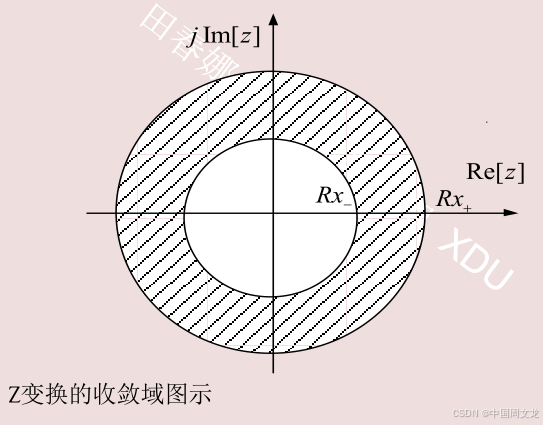
使 (3.2.2) 式成 立 , z 变量 取 值 的 域 称 为 收 敛 域 (Region of convergence, ROC) 。一般收敛域用环状区域来表示
常用的Z变换是一个有理函数,用两个多项式之比表示
分子多项式P(z)的根是X(z)的零点,记为zi(i = 1,2, …, M)分母多项式Q(z)的根是X(z)的极点,记为pk(k=1,2, …, N)在极点处Z变换不存在,因此收敛域中没有极点,收敛域总是用极点限定其边界
对比序 列 的DTFT和 Z变换 的定义,很容 易得到 二 者之间的关系:
1. 式中z=e jω表示在z平面上r=1的圆(单位圆)。
2.(3.2.3)式表明:单位圆上的Z变换就是序列的DTFT
3.如果已知序列的Z变换,可用(3.2.3)式,很方便的求出序列的DTFT,条件是收敛域中包含单位圆
例 3.2.1
x(n)=u(n),求其Z变换
极点是z=1,单位圆上的Z变换不存在,因此其DTFT不存在,但如果引入单位冲激函数,其DTFT则可以表示出来
该例同时说明一个序列的DTFT不存在,但在一定收敛域内Z变换是存在的
3.2.2 Z 变换收敛域的特性
由于 收 敛域 是 根 据幅 度 |z| 来确 定 的 ,所以 收 敛域 由 圆周来界定
右边序列(n<n0, x(n)=0)的收敛域总在半径为Rx-圆周的外部
左边序列(n>n0, x(n)=0)的收敛域总在半径为Rx+的圆周的内部
如果双边序列的收敛域存在,收敛域在 Rx-<|z|<Rx+ 的圆环上
有限长序列(n<n1 and n>n2, x(n)=0) 的收敛域是整个Z平面,如果n1<0, 那么z等于无穷不在收敛域内,如果n2>0,那么z=0不在收敛域内
由于X(z)在收敛域内一致收敛,收敛域不能包含极点
对于一个有理的X(z),至少有一个极点在收敛域的边界上
收敛域是一个连续的区域,收敛域不能由间断的几个区域组成
1. 有限长序列
如序列x(n)满足下式:
其Z变换为
设x(n)为有界序列,由于是有限项求和,除0与∞两点是否收敛 与n1、n2取值情况有关外,整个z平面均收敛
所以 的收敛域不包括∞点;
同理,如果n2>0, 则收敛域不包括z=0点;
如果是因果序列,收敛域包括z=∞点。具体有限长序列的收敛 域表示如下:
例3.2.2
求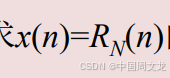
这是一个因果的有限长序列,因此收敛域为0。但由结果的分母可以看出似乎z=1是X(z)的极点,但同时分子多项式在z=1时也有一个零点,极零点对消,X(z)在单位圆上仍存在
2. 右序列
右序列是在n≥n1时, 序列值不全为零,而其它n1 ,序列值全为零
第一项为有限长序列,设n1≤-1,其收敛域为0≤|z|<∞。 第二项为因果序列,其收敛域为Rx-,Rx-是第二项最小的收敛半 径。
将两收敛域相与,其收敛域为Rx-。如果是因果序列,收敛域定为Rx- < |z|≤∞
例 3.2.3
解
在收敛域中必须满足|az -1 |, 因此收敛域为|z|>|a|
3. 左序列
左序列是在n≤n2时,序列值不全为零,而在n>n2,序列值全为 零的序列。左序列的Z变换表示为
例 3.2.4,
求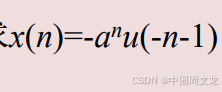
4. 双边序列
一个双边序列可以看作一个左序列和一个右序列之和,其Z变换表示为(n1>0)
X(z)的收敛域是X1 (z)和X2 (z)收敛域的公共收 敛区域
例 3.2.5
a为实数,求x(n)的Z变换及其收敛域
解:
第一部分收敛域为|az|<1,得|z|<|a|-1
第二部分收敛域为|az-1|<1,得到|z|>|a|
如果 |a|<1 , 即 |a|<|a|-1 , 两部 分 的 公 共 收 敛 域 为
|a|<|z|<|a|-1,其Z变换如下式:
如果|a|≥1,则无公共收敛域,因此X(z)不存在
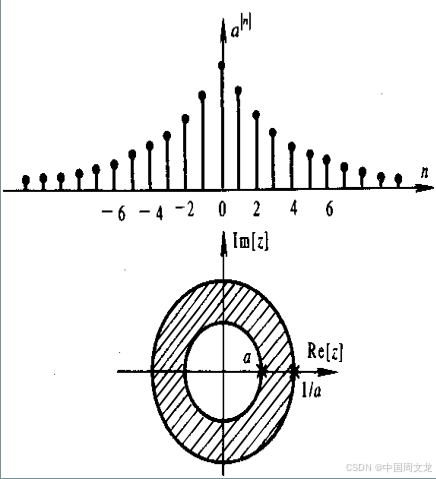
当0<a<1时,x(n)的波形及X(z)的收敛域如下图所示
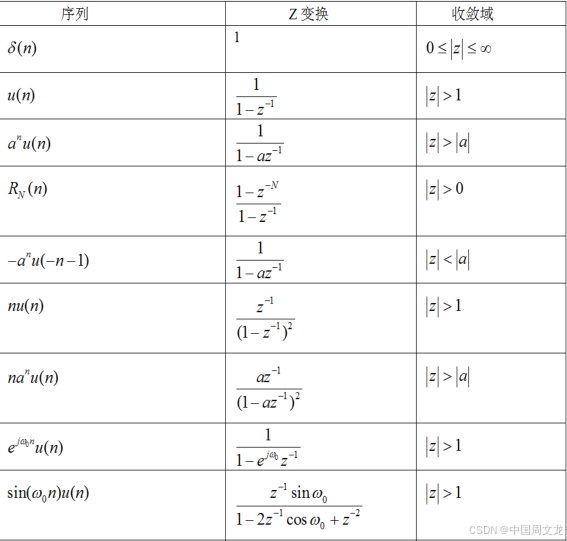
3.2.1常见序列的Z 变换及收敛域