图形学中Flood Fill是满水法填充,是用来填充区域的。就好比在一个地方一直到水,水会往四周满延开,直到高地阻挡。Flood Fill就是从一个点开始往四周寻找相同的点填充,直到有不同的点为止。
我们用的Flood Fill和这个差不多原理,就是BFS的一种形式.
假设在(i,j)滴好大一滴红墨水,然后水开始漫开,向它的上下左右染色,也就是(i-1,j),(i+1,j),(i,j-1),(i,j+1)这四个点.然后在分别再从这四个点开始向周围染色...直到碰到某种边界为止.
把这个转化为BFS的思想,就是队列中初始元素是(i,j),然后把(i,j)扩展状态,得到(i-1,j),(i+1,j),(i,j-1),(i,j+1)这四个状态,加入队列.把(i,j)出列,继续扩展下一个结点...如此
种子染色法
译 by Lucky Crazy & Felicia Crazy
(Flood Fill 按原意应翻译成“水流式填充法”(如果我没译错),有些中文书籍上将它称作“种子染色法”,然而大部分的书籍(包括中文书籍)都直接引用其英文原名:Flood Fill。介于此,下文所有涉及到Flood Fill的都直接引用英文 ——译者)
样例: 相连的农场Farmer John的农场被一次意外事故破坏了,有一些农场与其他的农场之间有道路相连,而有些道路却已被破坏。这使得Farmer John 无法了解到从一个农场能否到达另一个农场。你的任务就是帮助Farmer John来了解哪些农场是连通的。
给出:上题实际上就是要求寻找一张无向图的所有极大连通子图。
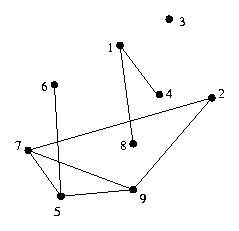
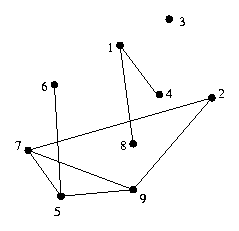
给出一张未知连通性的图,如下图:
可知,该图的极大连通子图是:{1,4,8}, {2,5,6,7,9} 和 {3}。
Flood Fill 可以用深度优先搜索,广度优先搜索或广度优先扫描来实现。他的实现方式是寻找到一个未被标记的结点对它标记后扩展,将所有由它扩展出的结点标上与它相同的标号,然后再找另一个未被标号的 结点重复该过程。这样,标号相同的结点就属于同一个连通子图。
深搜:取一个结点,对其标记,然后标记它所有的邻结点。对它的每一个邻结点这么一直递归下去完成搜索。
广搜:与深搜不同的是,广搜把结点加入队列中。
广度扫描(不常见):每个结点有两个值,一个用来记录它属于哪个连通子图(c),一个用来标记是否已经访问(v)。算法对每一个未访问而在某个连通子图当中的结点扫描,将其标记访问,然后把它的邻结点的(c)值改为当前结点的(c)值。
深搜最容易写,但它需要一个栈。搜索显式图没问题,而对于隐式图,栈可能就存不下了。
广搜稍微好一点,不过也存在问题。搜索大的图它的队列有可能存不下。深搜和广搜时间复杂度均为O(N+M)。其中,N为结点数,M为边数。
广度扫描需要的额外空间很少,或者可以说根本不要额外空间,但是它很慢。时间复杂度是O(N^2+M)。
(实际应用中,我们一般写的是DFS,因为快。空间不是问题,DFS可改用非递归的栈操作完成。但为了尊重原文,我们还是译出了广度扫描的全过程。——译者)
广度扫描的伪代码 代码中用了一个小技巧,因此无须额外空间。结点若未访问,将其归入连通子图(-2),就是代码里的component -2。这样无须额外空间来记录结点是否访问,请读者用心体会。
# component(i) denotes the
# component that node i is in
1 function flood_fill(new_component)
2 do
3 num_visited = 0
4 for all nodes i
5 if component(i) = -2
6 num_visited = num_visited + 1
7 component(i) = new_component
8 for all neighbors j of node i
9 if component(j) = nil
10 component(j) = -2
11 until num_visited = 0
12 function find_components
13 num_components = 0
14 for all nodes i
15 component(node i) = nil
16 for all nodes i
17 if component(node i) is nil
18 num_components =
num_components + 1
19 component(i) = -2
20 flood_fill(component
num_components)
算法的时间复杂度是 O(N 2),每个结点访问一次,每条边经过两次。
实例考虑刚才的那张图:
开始时,所有的结点都没有访问。(下例中未访问被表示为 -2)
首先从结点1开始,结点1未访问,那么先处理结点1,将它归入连通子图1。
标记完成后,对它进行第一步的扩展,由结点4和结点8与结点1连通,故它们被扩展出来。
之后,先处理结点4,将它与结点1归入相同的连通子图。现在它没有可扩展的结点了(结点1已被扩展过)
结点 连通子图 1 1 4 1 8
-2
接着处理结点8。结果与结点4一样。
现在,所有与结点1连通的结点都已扩展,标号为1的连通子图产生了。那么我们将跳出扩展步骤,寻找下一个连通子图,标号为2。
与上一步相同的顺序,找到结点2。
扩展结点2,结点7与结点9出现。
下一步,扩展结点7,结点5出现。
然后是结点9。
扩展结点5。结点6出现。
很遗憾,结点6没有可供扩展的结点。至此连通子图2产生。
之后寻找连通子图3,至此,仅有结点3未被扩展。
结点3没有可供扩展的结点,这样,结点3就构成了仅有一个结点的连通子图3。
结点3处理结束后,整个图的所有9个结点就都被归入相应的3个连通子图。Flood Fill 结束。
问题提示这类问题一般很清晰,求解关于“连通”的问题会用到 Flood Fill。它也很经常用作某些算法的预处理。
扩展与延伸有向图的连通性比较复杂。
同样的填充算法可以找出从一个结点能够到达的所有结点。每一层递归时,若一个结点未访问,就将其标记为已访问(表示他可以从源结点到达),然后对它所有能到达且为访问的结点进行下一层递归。
若要求出可以到达某个结点的所有结点,你可以对后向弧做相同的操作。
例题控制公司 [有删节, IOI 93]已知一个带权有向图,权值在0-100之间。
如果满足下列条件,那么结点A“拥有”结点B:
-
A = B
-
从A到B有一条权值大于50的有向弧。
-
存在一系列结点 C 1 到 C k 满足 A 拥有 C 1 到 C k, 每个节点都有一条弧到B,记作x 1 ,x 2 ...x k,并且 x 1 + x 2 + ... + x k> 50。
找出所有的(A,B)对,满足A拥有B。
分析:这题可以用上面提到的“给出一个源,在有向图中找出它能够到达的结点”算法的改进版解决。要计算A拥有的结点,要对每个结点计算其“控股百分比”。 把它们全部设为0。现在,在递归的每一步中,将其标记为属于A并把它所有出弧的权加到“控股百分比”中。对于每个“控股百分比”超过50的结点,进行同样 的操作(递归)。
街道赛跑 [IOI 95]
已知一个有向图,一个起点和一个终点。
找出所有的p,使得从起点到终点的任何路径都必须经过p。
分析:最简单的算法是枚举p,然后把p删除,看看是否存在从起点到终点的通路。时间复杂度为O(N (M + N))。题目的数据范围是 M <= 100, N <= 50,不会超时。
牛路 [1999 USACO 国家锦标赛, 有删节]连通图的直径定义为图中任意两点间距离的最大值,两点间距离定义为最短路的长。
已知平面上一个点集,和这些点之间的连通关系,找出不在同一个连通子图中的两个点,使得连接这两个点后产生的新图有最小的直径。
分析:找出原图的所有连通子图,然后枚举不在同一个连通子图内的每个点对,将其连接,然后找出最小直径。
笨蛋建筑公司Farmer John 计划建造一个新谷仓。不幸的是,建筑公司把他的建造计划和其他人的建造计划混淆了。Farmer John 要求谷仓只有一个房间,但是建筑公司为他建好的是有许多房间的谷仓。已知一个谷仓平面图,告诉Farmer John 它一共有多少个房间。