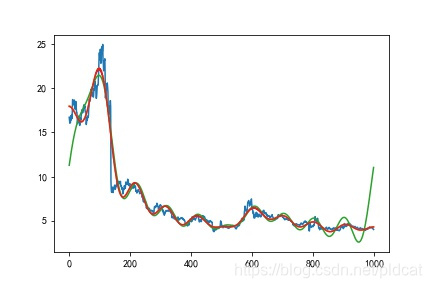
试图对数据进行傅里叶分析。但是对于实时序列预测,傅里叶分析的一个很严重的问题就是Gibbs现象。特别是在数据的末端,当数据被滤波重建时,由于DFT默认数据是周期性的,因此重建的数据序列第一个和最后一个趋于一致,如下图所示。
蓝色的原始数据,绿色的是DFT滤波重建的结果,红色的是DCT滤波重建的结果。可以看到DFT在滤波后重建函数在两端出现了严重的失真。这对于要分析和预测下一步的数据是致命的。因此必须设法解决这个Gibbs问题。
解决的方法就是延拓数据,最简单的一个方法就是把数据翻过来,加到原来数据后面,做fft滤波之后再截取需要部分的数据,这个方法就是dct.
这里先看一下我自己写的用fft实现的dct滤波函数。
def mydctfilter(y,n_min,n_max):
'''
使用离散余弦变换滤波。
参数:y:需要滤波的时间序列。
n_min,n_max:int,带通滤波器的最小频率和最大频率。这里的频率是指y的时间总长度的倒数,即n=1,为周期是y时间总长度的频率,
n=2为周期为y时间总长度/2的频率。
n值如果小于0或者大于N/2,N是y的序列长度,则直接返回y,不做变换。
n值为None表示不设上限或者下限,为低通或者高通滤波。
返回:
y_filter:滤波后还原的时间序列,虚部被抛弃,只返回实部。
'''
N = len(y)
halflen = int(N/2)
if n_min == None and n_max == None:
return y
if n_min == None:
n_min = 0
if n_max == None:
n_max = halflen
if n_min >= halflen or n_max > halflen:
return y
y_rev = y[::-1]
y_hat = np.concatenate((y,y_rev))
fft_y_hat = fft(y_hat)
#注意这里fft_y[0]是直流分量先拿出去,剩下的部分是对称的,即前面减几个后面就要减几个
if n_min != 0:
fft_y_hat[0:n_min-1] = 0
fft_y_hat[len(fft_y_hat)-n_min+2:] = 0
if n_max != N:
fft_y_hat[n_max+1:len(fft_y_hat)-n_max] = 0
y_filter = ifft(fft_y_hat)
print('y[0:5]: ',y_filter[:5])
print('y[N-5:N]',y_filter[N-5:])
print('y[300:305]',y_filter[300:305])
return y_filter[:N].real
再看一下使用dct函数实现的滤波:
def dctfilter(y,n_min,n_max):
'''
使用离散余弦变换滤波。
参数:y:需要滤波的时间序列。
n_min,n_max:int,带通滤波器的最小频率和最大频率。这里的频率是指y的时间总长度的倒数,即n=1,为周期是y时间总长度的频率,
n=2为周期为y时间总长度/2的频率。
n值如果小于0或者大于N/2,N是y的序列长度,则直接返回y,不做变换。
n值为None表示不设上限或者下限,为低通或者高通滤波。
返回:
y_filter:滤波后还原的时间序列,虚部被抛弃,只返回实部。
'''
N = len(y)
halflen = int(N/2)
if n_min == None and n_max == None:
return y
if n_min == None:
n_min = 0
if n_max == None:
n_max = halflen
if n_min >= halflen or n_max > halflen:
return y
dct_y = dct(y)
#注意这里dct_y[0]是直流分量先拿出去,剩下的部分是对称的,即前面减几个后面就要减几个
if n_min != 0:
dct_y[0:n_min-1] = 0
dct_y[len(dct_y)-n_min+2:] = 0
if n_max != halflen:
dct_y[n_max+1:N-n_max] = 0
y_filter = idct(dct_y)
print('y[0:5]: ',y_filter[:5])
print('y[N-5:N]',y_filter[N-5:])
print('y[300:305]',y_filter[300:305])
return y_filter.real
然而,两个函数的结果却是大相径庭。事实上,dctfilter恢复的数据是原数据的许多倍,显示的时候必须除上一个系数,才能显示出上面的图形。而且除上一个系数之后结果和mydctfilter相同。但是如果不滤波,使用idct也是可以完美重现原数据的。这是为什么?百思不得其姐,还是老办法,看原程序的说明。
Return the Discrete Cosine Transform of arbitrary type sequence x.
返回任意类型序列x的离散余弦变换
Parameters
参数
----------
x : array_like
The input array.
输入数组
type : {1, 2, 3, 4}, optional
类型:{1,2,3,4},可选
Type of the DCT (see Notes). Default type is 2.
DCT的类型(见说明)。默认类型是2.
n : int, optional
Length of the transform. If n < x.shape[axis], x is
truncated. If n > x.shape[axis], x is zero-padded. The
default results in n = x.shape[axis].
变换的长度,如果n < x.shape[axis],x 被截断。如果n > x.shape[axis],x填充0,默认结果是n = x.shape[axis].
axis : int, optional
Axis along which the dct is computed; the default is over the
last axis (i.e., axis=-1).
norm : {None, ‘ortho’}, optional
Normalization mode (see Notes). Default is None.
标准化模式(见说明),默认None
overwrite_x : bool, optional
If True, the contents of x can be destroyed; the default is False.
Returns
-------
y : ndarray of real
The transformed input array.
See Also
--------
idct : Inverse DCT
Notes
-----
For a single dimension array x, dct(x, norm='ortho') is equal to
MATLAB dct(x).
对于一维数组 x,dct(x, norm='ortho')等同于MATLAB的dct(x)。
There are, theoretically, 8 types of the DCT, only the first 4 types are
implemented in scipy. ‘The’ DCT generally refers to DCT type 2, and ‘the’ Inverse DCT generally refers to DCT type 3.
理论上,有8种不同类型的DCT,但是在scipy中只实现了4种。dct一般指第2种DCT,idct一般指第3种DCT。
Type I
类型1
There are several definitions of the DCT-I; we use the following
(for norm=None)
DCT-1有几种定义,我们使用以下的(norm=None的情形)
y
k
=
x
0
+
(
−
1
)
k
x
N
−
1
+
2
∑
n
=
1
N
−
2
x
n
cos
(
π
k
n
N
−
1
)
y_k = x_0 + (-1)^k x_{N-1} + 2 \sum_{n=1}^{N-2} x_n \cos\left( \frac{\pi k n}{N-1} \right)
yk=x0+(−1)kxN−1+2n=1∑N−2xncos(N−1πkn)
If norm='ortho', x[0] and x[N-1] are multiplied by a scaling
factor of :
2
\sqrt{2}
2, and y[k] is multiplied by a scaling factor f
如果norm='ortho',x[0] 和x[N-1]被乘上系数
2
\sqrt{2}
2,y[k]被乘上系数f
f
=
{
1
2
1
N
−
1
if
k
=
0
or
N
−
1
,
1
2
2
N
−
1
otherwise
f = \begin{cases} \frac{1}{2}\sqrt{\frac{1}{N-1}} & \text{if }k=0\text{ or }N-1, \\ \frac{1}{2}\sqrt{\frac{2}{N-1}} & \text{otherwise} \end{cases}
f=⎩⎨⎧21N−1121N−12if k=0 or N−1,otherwise
… versionadded:: 1.2.0
Orthonormalization in DCT-I.
正交归一化
… note::
The DCT-I is only supported for input size > 1.
Type II
类型2
There are several definitions of the DCT-II; we use the following
(for norm=None)
类型2有多种定义,我们使用以下定义(norm=None的情形)
y
k
=
2
∑
n
=
0
N
−
1
x
n
cos
(
π
k
(
2
n
+
1
)
2
N
)
y_k = 2 \sum_{n=0}^{N-1} x_n \cos\left(\frac{\pi k(2n+1)}{2N} \right)
yk=2n=0∑N−1xncos(2Nπk(2n+1))
If norm='ortho', y[k] is multiplied by a scaling factor f
如果norm='ortho',y[k]就要乘上一个尺度因子f
f
=
{
1
4
N
if
k
=
0
,
1
2
N
otherwise
f = \begin{cases} \sqrt{\frac{1}{4N}} & \text{if }k=0, \\ \sqrt{\frac{1}{2N}} & \text{otherwise} \end{cases}
f=⎩⎨⎧4N12N1if k=0,otherwise
which makes the corresponding matrix of coefficients orthonormal
(O @ O.T = np.eye(N)).
这样做的结果是协相关矩阵的系数归一正交化 (O @ O.T = np.eye(N)).
**Type III**
类型三
There are several definitions, we use the following (for ``norm=None``)
有多种定义,我们采用以下定义(norm=None的情形)
y
k
=
x
0
+
2
∑
n
=
1
N
−
1
x
n
cos
(
π
(
2
k
+
1
)
n
2
N
)
y_k = x_0 + 2 \sum_{n=1}^{N-1} x_n \cos\left(\frac{\pi(2k+1)n}{2N}\right)
yk=x0+2n=1∑N−1xncos(2Nπ(2k+1)n)
or, for norm='ortho'
或者,norm=‘ortho’的情形:
y
k
=
x
0
N
+
2
N
∑
n
=
1
N
−
1
x
n
cos
(
π
(
2
k
+
1
)
n
2
N
)
y_k = \frac{x_0}{\sqrt{N}} + \sqrt{\frac{2}{N}} \sum_{n=1}^{N-1} x_n \cos\left(\frac{\pi(2k+1)n}{2N}\right)
yk=Nx0+N2n=1∑N−1xncos(2Nπ(2k+1)n)
The (unnormalized) DCT-III is the inverse of the (unnormalized) DCT-II, up
to a factor 2N. The orthonormalized DCT-III is exactly the inverse of
the orthonormalized DCT-II.
未标准化的DCT-3是未标准化的DCT-2的逆。归一正交化的DCT-3是归一正交化的DCT-2的逆变换。
Type IV
类型4
There are several definitions of the DCT-IV; we use the following
(for norm=None)
norm=None的情形:
y
k
=
2
∑
n
=
0
N
−
1
x
n
cos
(
π
(
2
k
+
1
)
(
2
n
+
1
)
4
N
)
y_k = 2 \sum_{n=0}^{N-1} x_n \cos\left(\frac{\pi(2k+1)(2n+1)}{4N} \right)
yk=2n=0∑N−1xncos(4Nπ(2k+1)(2n+1))
If norm='ortho', y[k] is multiplied by a scaling factor f
如果norm=‘ortho’,y[k]被乘上尺度因子f
f
=
1
2
N
f = \frac{1}{\sqrt{2N}}
f=2N1
… versionadded:: 1.2.0
Support for DCT-IV.
References
----------
… [1] ‘A Fast Cosine Transform in One and Two Dimensions’, by J.
Makhoul, IEEE Transactions on acoustics, speech and signal processing vol. 28(1), pp. 27-34,
:doi:10.1109/TASSP.1980.1163351 (1980).
… [2] Wikipedia, “Discrete cosine transform”,
https://en.wikipedia.org/wiki/Discrete_cosine_transform
Examples
--------
The Type 1 DCT is equivalent to the FFT (though faster) for real,
even-symmetrical inputs. The output is also real and even-symmetrical.
Half of the FFT input is used to generate half of the FFT output:
>>> from scipy.fftpack import fft, dct
>>> fft(np.array([4., 3., 5., 10., 5., 3.])).real
array([ 30., -8., 6., -2., 6., -8.])
>>> dct(np.array([4., 3., 5., 10.]), 1)
array([ 30., -8., 6., -2.])
好了,上面这些说的是什么?为什么我从字里行间里只看到了懵圈两个字。呵呵,其实里面还是有不少东西的。让我们来解读一下:
1、那个归一正交化很重要,就是norm=‘ortho’。人家已经告诉你了,不加这个参数,这些cos的基是不正交的。测试一下,上面代码里的dct和idct都加上norm=‘ortho’,果然最初的问题解决掉了。其实人家开头就告诉你了:dct(x, norm=‘ortho’)相当于MATLAB的dct(x),sci就是这么坑,这样一个参数居然不是缺省的。
2、那个什么4种类型,8种类型的到底是个啥。这个似乎、可能、大概不是多么重要。它说的应该是关于x0和xn的边界条件怎么用的问题,对结果的影响应该不大。而且也告诉你了:一般用第二种就行了,第三种是它的idct变换。这四种类型的区别似乎在于周期延拓的时候x0和xn的应用。类型一是x0和xn都作为偶对称的轴,即通过偶对称延拓数据,但x0和xn是不动的。类型2的轴对称点则是-1/2和n-1/2,就是说延拓的时候x0和xn在对称面也会复制一个。类型3的轴是x0xn但x0是偶对称,xn是奇对称。类型四的轴是-1/2和n-1/2,但-1/2是偶对称,n-1/2是奇对称。我的理解是这样,不一定对,大神指正一下。
3、第三点是上面的说明里没有的,就是dct产生的频谱的频率变了。如果我们把dct理解成偶对称延拓后的数值序列的fft分析结果,那么里面显然存在一个问题,那就是:fft的每一个数字代表的是在整个数据周期中震荡1次的频率,然而在dct中这个周期变成了两倍,因此fft_y的每一个数字代表的频率也应降低一倍。实际上,上面的图是用下面的代码生成的:
N = len(y)
x = np.arange(N)
plt.plot(x,y)
plt.plot(x,mydctfilter(y,None,20))
plt.plot(x,fouriorfilter(y,None,10))
#b = np.max(dctfilter(y,None,20))/np.max(mydctfilter(y,None,20))
#print('b:',b)
plt.plot(x,dctfilter(y,None,20))
图中用傅里叶滤波的曲线和用dct滤波的曲线除了头尾因为Gibbs现象有差别,其余是很接近的。但是注意滤波所选的频率是差了一倍的,如果用相同的数字,曲线会有很大的不同。