后缀表达式转中缀表达式

在学习《数据结构与算法分析》时，第3章有一个练习题，第1问要求编写程序将中缀表达式转换成后缀表达式，这个还是容易的，因为书上已经给了详细的思路，用栈就可以了，实现方法在我另一篇博客里有写到-中缀表达式转后缀表达式。这题最后一问是让把后缀表达式转换成中缀表达式，这个还是有点难度的，当时是想按计算后缀表达式的方法得到中缀表达式，思路很简单，也很好实现，但这样会出现一个问题——转换结果里有多余的括号，比如会产生（（a+b）+（c+d））这样的结果，或者（a+（b*（c*d）））这样的结果，计算结果里的很多括号都是多余的，看着很不舒服，但也没想到好的解决办法，所以当时就暂时把这个问题搁置了。

在看到第4章，二叉树那一节时，书上介绍了一种将后缀表达式转换成二叉树的方法：即一次一个符号地读入表达式，如果符号是操作数，那么就建立一个单节点树并将一个指向它的指针推入栈中。如果符号是操作符，那么就从栈中弹出指向两棵树T1和T2的那两个指针（T1的先弹出）并形成一颗新的树，该树的根就是操作符，它的左右儿子分别指向T1和T2。然后将指向这颗树的指针压入栈中。书上有具体的例子，我就不再赘述。转换完成后，我们只要中序遍历该树，并加上相应的括号，就完成了后缀表达式到中缀表达式的转换。

树的结构和栈的结构：

struct TreeNode
{
	ElementType Element;
	Tree		Left;
	Tree		Right;
};

struct StructNode
{
	PstToNode	Next;
	PtrToNode	PtrTree;
};

后缀表达式转换为树：

Tree PostfixToTree(char *str)
{
	Tree T,Tmptree;
	Stack S;

	T = CreatTree();
	S = CreatStack();
	for (int i = 0; str[i] != '\0'; i++)
	{
		/*如果符号是操作数*/
		if (!IsSymbol(str[i]))
		{
			Tmptree = CreatTree();
			Tmptree->Element = str[i];
			Push(Tmptree, S);
		}
		/*如果符号是运算符*/
		else
		{
			Tmptree = CreatTree();
			Tmptree->Element = str[i];
			Tmptree->Right = TopAndPop(S);
			Tmptree->Left = TopAndPop(S);
			Push(Tmptree, S);
		}
	}
	T = TopAndPop(S);

	return T;
}

下面的任务就是把树转换成中缀表达式了。前面已经说过，中序遍历树即可得到中缀表达式，但得到的是错误的、不带括号的表达式，那么如何在表达式中加入括号呢？

这个问题我一开始是想从中序遍历树的程序入手，下面是我找到的两个程序，一个是递归中序遍历，一个是非递归中序遍历。

/*中序遍历二叉树-递归*/
void InOrder_R(Tree T)
{
	if (T)
	{
		InOrder_R(T->Left);		 // 遍历左子树  
		printf("%c", T->Element);// 访问结点  
		InOrder_R(T->Right);		 // 遍历右子树  
	}
}

/*中序遍历二叉树-非递归*/
void InOrder_NR(Tree T)
{
	Tree Tmptree = T;//当前访问节点
	Stack S = CreatStack();//创建一个空栈

	//直到当前节点为NULL且栈空时，循环结束
	while (!(Tmptree == NULL && IsEmpty(S)))
	{
		//如果Tmptree的左孩子不为空，则将其入栈，并置其左孩子为当前节点
		if (Tmptree->Left != NULL)
		{
			Push(Tmptree, S);
			Tmptree = Tmptree->Left;
		}
		//如果Tmptree的左孩子为空，则输出Tmptree节点，并将其右孩子设为当前节点，看起是否为空
		else
		{
			printf("%c", Tmptree->Element);
			Tmptree = Tmptree->Right;
			//如果为空，且栈不空，则将栈顶节点出栈，并输出该节点
			//同时将它的右孩子设为当前节点，继续判断，直到当前节点不空
			while (Tmptree == NULL && !IsEmpty(S))
			{
				Tmptree = TopAndPop(S);
				printf("%c", Tmptree->Element);
				Tmptree = Tmptree->Right;
			}
		}
	}
}

显然，递归的程序非常简单，简单到无法插入括号。。。

非递归的程序相对复杂，具体原理这里不多说，但要适当的插入括号的话，也是无法下手。。。

最后我干脆把这两个都删了，重新想了一个办法，总体思路使用递归实现括号的添加，具体如下：

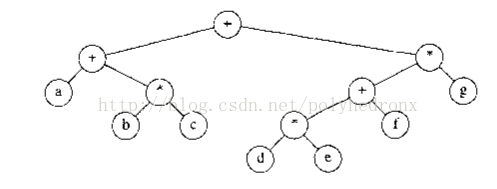
这是中缀表达式 a+b*c+(d*e+f)*g 的二叉树形式。

以上图为例，采用递归的思想，假设我们已经写出了一个将二叉树转换成中缀表达式的程序：

1.对于根节点“+”，我们可以先计算出其左边分支的中缀表达式和右边分支的中缀表达式；

2.然后把左右两部分以“+”号连接起来即可；

3.依次递推，就可得到整个树的中缀表达式。

4.括号的添加方法：

（1）对于当前节点，如果其左节点是操作符，且运算优先级小于当前节点操作符，则给左子树的中缀表达式加括号；

（2）对于当前节点，如果其右节点是操作符，且运算优先级不大于当前节点操作符，则给右子树的中缀表达式加括号。

程序如下：

/*树转换为中缀表达式*/
char *TreeToInfix(Tree T)
{
	char* tep  = (char*)calloc(2, sizeof(char*));
	char* str  = (char*)calloc(100, sizeof(char*));
	char* strl = (char*)calloc(100, sizeof(char*));
	char* strr = (char*)calloc(100, sizeof(char*));
	//初始化
	strcpy(str , "\0");
	strcpy(strl, "\0");
	strcpy(strr, "\0");

	if (T)
	{
		strl = TreeToInfix(T->Left); //当前节点左子树的中缀表达式
		strr = TreeToInfix(T->Right);//当前节点右子树的中缀表达式

		if (T->Left)
		{
			//如果左节点是运算符且优先级小于当前节点，则给左子树的中缀表达式加括号
			if (IsSymbol(T->Left->Element) && ComparePri(T->Element, T->Left->Element))
				strl = Brackets(strl);
		}
		if (T->Right)
		{
			//如果右节点是运算符且优先级不大于当前节点，则给右子树的中缀表达式加括号
			if (IsSymbol(T->Right->Element) && !ComparePri(T->Right->Element, T->Element))
				strr = Brackets(strr);
		}
		//把左右两部分和当前节点连接起来
		*tep = T->Element;
		strcat(str, strl);
		strcat(str, tep);
		strcat(str, strr);
	}
	//返回以当前节点作为根节点的树转换成的中缀表达式
	return str;
}

不得不说，递归真的是赏心悦目啊！

下面是主程序中用到的几个子程序：

/*判断是否为运算符*/
int IsSymbol(char c)
{
	return c == '+' || c == '-' || c == '*' || c == '/' || c == '(' || c == ')';
}

/*计算优先级*/
int Priority(char c)
{
	switch (c)
	{
	case '*':
	case '/':return 1;
	case '+':
	case '-':return 0;
	default: return -1;
	}
}

/*比较优先级*/
int ComparePri(char x, char y)
{
	return Priority(x) > Priority(y) ? 1 : 0;
}

/*给字符串加括号*/
char *Brackets(char *str)
{
	char* s = (char*)calloc(100, sizeof(char*));
	strcpy(s, "\0");
	strcat(s, "(");
	strcat(s, str);
	strcat(s, ")");
	return s;
}

至此，所有的问题都解决了，来一波测试：

int main(void)
{
	char *ans;
	char str[100];	
	while (scanf_s("%s", str, sizeof(str)) != NULL)
	{
		ans = PostfixToInfix(str);
		printf("ans = ");
		printf("%s\n", ans);
	}
}

测试结果：

结果很完美啊有木有！

可能有的童鞋注意到了测试结果里面的第二个例子好像多了个括号，其实没错，那是为了保证运算次序的。因为如果不加括号就是（a+b）先乘c再乘（d+e）了，但从后缀表达式我们也能看出来，真实的运算次序是c先乘（d+e），然后再和（a+b）相乘。

后缀表达式转中缀表达式

悦读