一、了解二叉搜索树
二叉搜索树就是任意一个根节点的值比左孩子的值大,比右孩子的值小的树。
所以中序遍历二叉搜索树得到的是从小到大的数组。
当然普通的二叉搜索树搜索时间不一定是O(logN),当以有序的顺序插入普通二叉搜索树时,得到的是一个单支的搜索树,此时查找值就是O(N),所以才有后面的 AVL 树和红黑树。
今天实现普通二叉搜索树。
二、部分代码展示
#pragma once
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V> _left;
BSTreeNode<K, V> _right;
K _key;
V _val;
BSTreeNode(const K& key, const V& val)
:_key(key)
,_val(val)
,_left(nullptr)
,_right(nullptr)
{ }
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
bool insert(const K& key, const V& val)
{
if (_root == nullptr)
{
_root = new Node(key, val);
return true;
}
Node* cur = _root;
Node* prev = nullptr;
while (cur)
{
if (cur->_key > key)
{
prev = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
prev = cur;
cur = cur->_right;
}
else
return false;
}
Node* newnode = new Node(key, val);
key > prev->_key ? prev->_right = newnode : prev->_left = newnode;
return true;
}
Node* find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
cur = cur->_left;
else if (cur->_key < key)
cur = cur->_right;
else
return cur;
}
return nullptr;
}
// 删除从孩子情况考虑
bool erase(const K& key)
{
// 1.先找指定节点
Node* cur = _root;
Node* prev = cur;
while (cur)
{
if (cur->_key < key)
{
prev = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
prev = cur;
cur = cur->_left;
}
else
{
// 2.若没有孩子或只有一个孩子
// 问题:如果删的是头节点,头节点没有父亲,只能另外判断
if (cur->_left == nullptr || cur->_right == nullptr)
{
if (cur->_left)
{
if (_root == cur)
_root = cur->_left;
else
cur == prev->_left ? prev->_left = cur->_left : prev->_right = cur->_left;
}
else
{
if (_root == cur)
_root = cur->_right;
else
cur == prev->_left ? prev->_left = cur->_right : prev->_right = cur->_right;
}
delete cur;
}
// 3.有两个孩子,替代法,找左树的最右边或右树的最左边,交换删除节点和前面两个的任意一个
// 不要忘记交换的节点的孩子
// 若被删节点的右子树的最左节点一开始不存在会导致两个问题:
// 第一,循环进不去,rightMinP不会更新,所以一开始rightMinP就要是rightMin的父节点cur
// 第二,正常如果有rightMin->_left,rightMin在rightMinP的左边,如果没有就在右边
// 所以最后更新一个是P的左子树等于rightMin右子树,一个是右子树等于右子树
else
{
Node* rightMin = cur->_right;
Node* rightMinP = cur;
while (rightMin->_left)
{
rightMinP = rightMin;
rightMin = rightMin->_left;
}
std::swap(cur->_key, rightMin->_key);
// 由于是右树的左孩子,所以只要关心他的右孩子
if(rightMin == rightMinP->_left)
rightMinP->_left = rightMin->_right;
else
rightMinP->_right = rightMin->_right;
delete rightMin;
}
return true;
}
}
return false;
}
private:
Node* _root = nullptr;
};
三、插入函数
1、思路
插入很简单,比根大向右走,比根小向左走,遇到空就插入。
2、问题
(1)遇到相等?
一般的二叉搜索树不支持存储相等 key,所以直接返回 false
(2)一开始根节点是 nullptr?
添加根节点为插入值。
四、删除函数
1、思路
| 情况 | 措施 |
| 删除节点没有孩子 | 父节点指向空 |
| 删除节点有一个孩子 | 父节点指向删除节点的唯一孩子 |
| 删除节点有两个孩子 | 替换法 |
替换法:在删除节点的孩子中找到能顶替删除节点的,那必须是比原本左子树的根大,比右子树的根小,那就是右子树的最左节点或左子树的最右节点,代码里展示的是右子树的最左节点。找到后和删除节点交换值,然后把右子树最左节点的右孩子(都是最左节点了肯定只有一个右孩子)交给他的父节点。
优化:节点只有一个孩子和没有孩子的情况可以一起考虑,因为当没有右孩子时就让父节点指向左孩子,此时如果删除节点没有孩子,左孩子也是空,不影响结果,同理没有左孩子也是一样。所以是没有孩子的情况可以复用只有一个孩子情况的代码。
2、问题
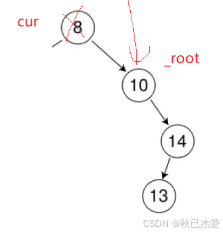
(1)一开始删除的是根节点且根节点孩子少于两个?
如下图:
由于根节点没有父亲,所以不做判断会出错。把 _root 传给下一个孩子就行了。
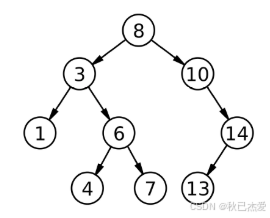
(2)一开始删除节点的右子树没有最左节点?
如果一开始删除节点的右子树有最左节点,即我们现在要删3
那我们首先要找右子树最左节点,定义 rightMin 是6,rightMin 的父节点 rightMinP 是3,最后经过循环找到右子树的最左节点是4,即此时 rightMin 是4,rightMinP是6
接下来逻辑是 swap(cur->_val, rightMin->_val); rightMinP->_left = rightMin->_right;
但是上面的逻辑并不适用于一开始没有左子树的情况,即现在我们要删10
没有左子树会出现两个问题:
a、找左子树的循环进不去,父节点不更新。
所以我们一开始定义 rightMinP 是 cur,即8
b、此时删除节点的右孩子充当了右子树的最左节点
但是上面的代码 rightMinP->_left = rightMin->_right; 逻辑明显有问题。
应该是 rightMinP->_right = rightMin->_right; 需要特判解决。