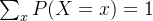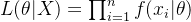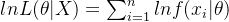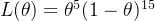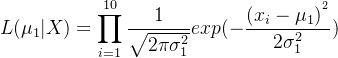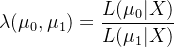声明:本文章是根据网上资料,加上自己整理和理解而成,仅为记录自己学习的点点滴滴。可能有错误,欢迎大家指正。
在机器学习和统计学领域中,似然函数(Likelihood Function)是一个至关重要的概念。它不仅是参数估计的基础,而且在模型选择、模型评估以及众多先进的算法和技术中都有着广泛的应用。
1. 似然VS概率
概率和似然是统计学中两个不同的概念,它们在概念上和应用上都有所区别。以下是通过一个具体例子来展示这两者之间的区别:
1.1 概率(Probability)
定义:概率是在给定的参数下,某个事件发生的可能性。它是未来事件发生的度量,通常用介于0和1之间的数值表示。
例子:假设我们有一个标准的六面骰子,每个面上有1到6的数字。当我们掷骰子时,得到数字6的概率是:𝑃(数字=6)=1/6
在这个例子中,参数是骰子的面数(6面),事件是掷出数字6,概率是已知的,并且是在掷骰子之前就确定的。这里的关键是,概率是在给定参数(骰子的公平性,即所有面出现概率相同)的情况下,事件发生的可能性。
1.2 似然(Likelihood)
定义:似然是在已知观测数据的情况下,这些数据对于不同参数值的支持程度。它不是数据发生的概率,而是在给定数据时参数值的相对合理性。
现在,假设我们不确定骰子是否公平,我们通过掷骰子20次,观察到数字6出现了5次。我们想要估计掷出数字6的真实概率 𝜃:
- 似然函数 表示为 𝐿(𝜃∣5次6),是 𝜃 的函数,表示在参数 𝜃下观测数据(5次6)的相对可能性。似然函数是: 𝐿(𝜃∣5次6)=
。
- 对𝜃的求解,可用最大似然方法,具体可看后面,这时求出的𝜃的值不一定是1/6。
对比上面的例子:
概率函数 给出了在给定参数下事件发生的可能性。在我们的例子中,它告诉我们在假设骰子公平的情况下,掷出6的概率是 1/6。
似然函数 用于在已知观测数据的情况下,评估不同参数值的合理性。在我们的例子中,它帮助我们根据观测到的5次6来估计 𝜃 的值。
1.3 两者区别:
- 概率是已知参数下事件的度量:在概率中,参数是已知的,我们计算的是某个事件发生的可能性。
- 似然是已知数据下参数的度量:在似然中,数据是已知的,我们评估的是不同参数值对数据的支持程度。
- 概率是绝对的:概率给出了在给定参数下事件发生的确切概率。
- 似然是相对的:似然比较了在已知数据下,不同参数值的相对合理性。
总结来说,概率关注的是在给定参数下事件发生的可能性,而似然关注的是在给定数据下参数值的合理性。这两者在统计分析中扮演着不同的角色。
2. 概率函数VS似然函数
2.1 概率函数(Probability Function, PF)
-
定义:概率函数是描述随机变量取各种可能值的概率。对于离散随机变量,它是一个定义在所有可能结果上的函数;对于连续随机变量,它是一个概率密度函数。
-
用途:概率函数用于计算在给定参数下,随机变量取特定值或处于某个区间的概率。
(1)概率函数
- 对于离散型随机变量,概率函数通常指的是概率质量函数(Probability Mass Function, PMF),它给出了随机变量取每个可能值的概率.
-
对于离散随机变量 X,概率函数可以表示为
,满足以下性质:。
- 非负性:对于所有的 𝑥x,有 𝑃(𝑋=𝑥)≥0。
- 归一性:所有可能的 𝑥x 上的概率之和为1,即:
- 对于连续随机变量 X
(2) 概率密度函数(Probability Density Function, PDF)
- 概率密度函数是用于描述连续型随机变量在某个值或某个区间内取值的概率的函数。
- 对于连续型随机变量 X,其概率密度函数
表示为
,其中
是累积分布函数满足以下性质:
- 非负性:对于所有的 𝑥,有 𝑓(𝑥)≥0。
- 归一性:𝑋的整个取值范围内,概率密度函数的积分总和为1,即:
2.2 似然函数(Likelihood Function, LF)
-
定义:似然函数是在已知观测数据的情况下,这些数据对于不同参数值的相对可能性。它是参数的函数,用于估计参数。
-
用途:似然函数用于参数估计,特别是在最大似然估计中,通过找到使似然函数最大化的参数值。
-
数学表示:对于简单随机样本,似然函数可以表示为观测数据的概率函数的乘积:
其中,𝜃 是参数,
是观测值,
是给定参数 𝜃下第 𝑖个观测值的概率密度函数或概率质量函数。
2.3 两者区别:
- 参数与数据的角色:在概率函数中,参数是已知的,数据是随机的;而在似然函数中,数据是已知的,参数是未知的。
- 目的:概率函数用于计算特定事件发生的概率,似然函数用于估计模型参数。
- 形式:概率函数通常与特定的概率分布相关联(如正态分布、二项分布等),而似然函数是观测数据对参数的函数。
例子:假设我们有一个骰子,并且想知道掷出6点的概率 𝜃。
- 概率函数:如果我们假设骰子是公平的,那么掷出6点的概率函数是 𝑃(6点)=𝜃=1/6。
- 似然函数:若我们掷了20次,观察到5次6点,似然函数将是
。我们通过最大化这个似然函数来估计 𝜃 的值。
3.最大似然估计
极大似然估计(Maximum Likelihood Estimation, MLE)是一种在已知观测数据的情况下估计概率模型参数的方法。它基于以下原则:
-
似然函数:首先定义似然函数,它是在给定参数值
下观测数据
的概率。对于独立同分布的观测数据
,似然函数可以表示为所有观测数据
的概率密度函数(对于连续型随机变量)或概率质量函数(对于离散型随机变量)的乘积:
-
最大化似然:然后,选择使似然函数达到最大值的参数
。这些参数值被称为极大似然估计值。
-
对数转换:为了简化计算,通常对似然函数取对数,因为对数是单调函数,可以将乘积转换为求和:
-
求解参数:对对数似然函数求导,并找到导数为零的点,这通常涉及到数值优化技术。
-
统计性质:在大样本情况下,极大似然估计具有一些良好的统计性质,如一致性(估计值随着样本量的增加而趋近于真实值)和渐近正态性(估计量的分布趋近于正态分布)。
仍然是上面的例子:现在,假设我们不确定骰子是否公平,我们通过掷骰子20次,观察到数字6出现了5次。我们想要估计掷出数字6的真实概率 𝜃:
写出似然函数:根据观测结果(例如,掷20次得到5次6),写出似然函数:
取对数:为了简化计算,通常对似然函数取对数,得到对数似然函数:
求导数:对 𝜃 求导,并找到导数为零的点,这通常通过设置导数等于零并解方程来完成:
解方程:解上述导数等于零的方程,得到 𝜃 的值:
,可得
得到最大似然估计:解得
或 0.25,这就是掷出数字6的最大似然估计概率。
如果骰子是完全公平的,我们期望 θ 接近 1/6,但由于我们的样本数据,我们得到的估计值是 1/4。这可能表明骰子存在偏差,或者仅仅是由于随机变异。
4. 似然比
似然比(Likelihood Ratio)是统计学中用于比较两个统计模型对同一数据集的拟合优度的量。它是两个似然函数值的比率,通常用于模型选择、假设检验和参数估计中。
定义:
似然比 𝜆λ 可以定义为两个模型的似然函数值的比值: 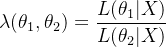
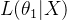
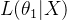
应用:
- 模型选择:在比较两个模型时,似然比可以用来评估哪个模型对数据的拟合更好。
- 似然比检验:一种统计假设检验方法,用于比较零假设(𝐻0H)和备择假设(𝐻1)下的似然函数值。
例子:假设我们有一个简单的数据集,由10个观测值组成,我们想要比较以下两个模型:
- 模型1(零假设 𝐻0): 假设观测值来自均值为
,标准差为
的正态分布。
- 模型2(备择假设 𝐻1): 假设观测值来自均值为
,标准差为
的正态分布。
假设我们观测到的数据是 X={2,3,4,5,6,7,8,9,10,11}。
计算似然函数:首先,我们为每个模型计算似然函数。假设
和
是已知的,我们只估计均值 𝜇。
模型1的似然函数(假设
):
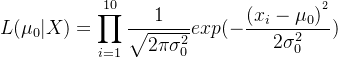
模型2的似然函数(假设
):
计算似然比:
评估似然比:如果似然比 𝜆 接近1,说明两个模型对数据的拟合程度相似;如果 𝜆 显著大于1,模型1可能更合适;如果 𝜆显著小于1,模型2可能更合适。
似然比检验:在实际应用中,我们通常对数化似然比,并将其与特定的统计量进行比较,以决定是否拒绝零假设。
通过这个例子,我们可以看到似然比如何用于比较不同模型对同一数据集的拟合优度,并在模型选择和假设检验中发挥作用。