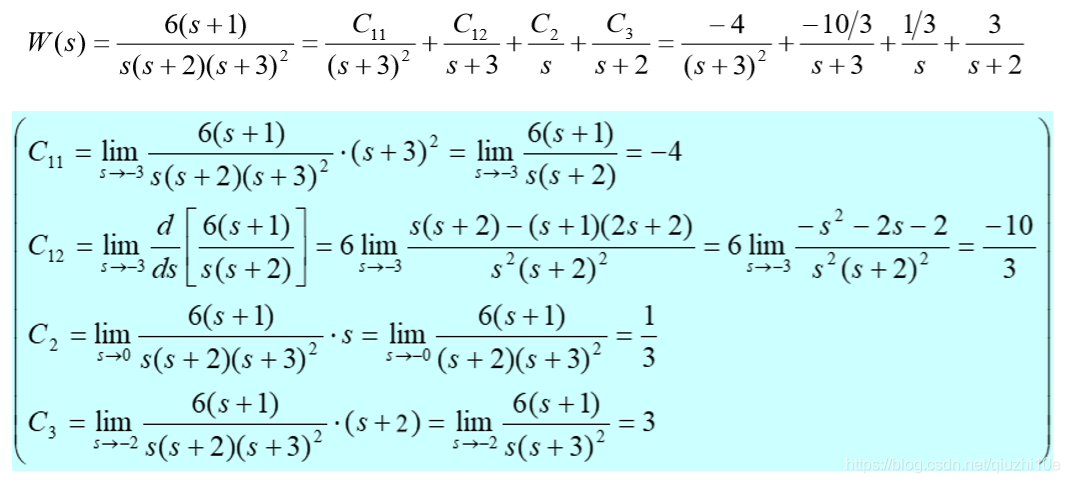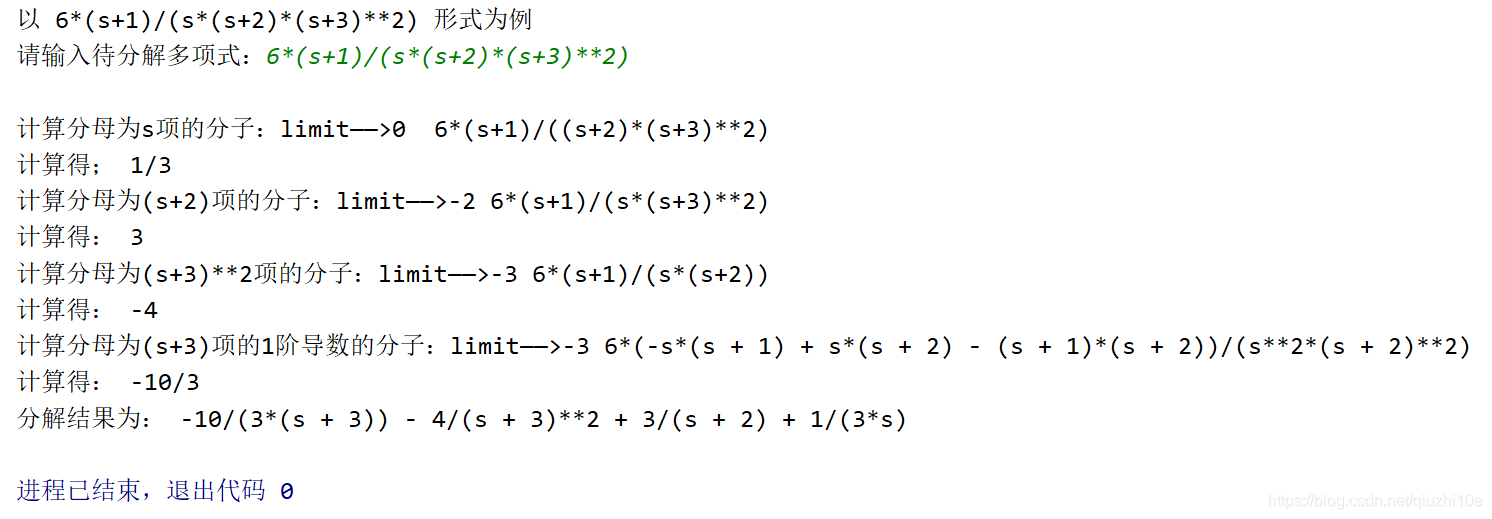编写之初

由于利用留数定理分解分式多项式的计算麻烦，所以决定用python做一个利用留数定理分解分式多项式程序，实现只要输入多项式就可以得到各种中间参数和最终拆分结果的目的。从本程序可以得到：分解后每项多项式分子值、计算分解后每项多项式分子值的过程展示、最终分解结果展示。

算数实现

利用留数定理分解分式多项式计算过程以下图为例所示

对于算数运算形象的理解：以该式为例，分解后各项分母为原多项式分母中的各项（s、(s+2)、(s+3)²）加上这些项中高次幂项去掉次幂为分母的项（(s+3)）;分解后各项分子为原多项式分母依次去掉各项后求极限所得值（-4、1/3、3）以及n(n>1)次幂项去掉该项后的n阶微分式求极限所得值（-10/3）。也依据这个思路编写程序。

依赖的包

1.sympy模块
sympy模块，可以进行符号计算，可以定义符号变量，进行代数运算，以及微分运算、积分运算等。

pip install sympy

2.re正则化模块
re模块是python独有的匹配字符串的模块，该模块中提供的很多功能是基于正则表达式实现的。

pip install re

完整代码及注释

import sympy as sp
import re

s = sp.symbols('s')     # 创建符号变量

print('以 6*(s+1)/(s*(s+2)*(s+3)**2) 形式为例')
Y = input('请输入待分解多项式：')   # 复制 例 6*(s+1)/(s*(s+2)*(s+3)**2)

# denominator = y.split('/')[0]   # 分子项
molecule = Y.split('/')[1]      # 分母项

moleculelist = molecule.strip('()').split('*')  # 分母每项
# print(moleculelist)

reg = re.compile(r"(?<=\*)\d+")     # 获取分式中的幂数
match=reg.search(Y)
pow = match.group(0)

molecule_number = 0     # 初始化分母项索引
# 计算拆分后各项值
while molecule_number < len(moleculelist):
    try:
        if moleculelist[molecule_number] != '':
            if moleculelist[molecule_number + 1] != '':
                y = Y.replace(moleculelist[molecule_number]+'*', '')    # 得到用来计算 该项分子值 的多项式
                if moleculelist[molecule_number] == 's':
                    value = sp.limit(y, s, 0)               # 求极限计算 该项分子值
                    print('\n计算分母为' + str(moleculelist[molecule_number]) +'项的分子：limit——>0 ', y)
                    print('计算得；', value)
                else:
                    limit_value = -int(re.findall('(\d+)', moleculelist[molecule_number])[0])   # 获取求极限时的 极限参数
                    value = sp.limit(y, s, limit_value)         # 求极限计算 该项分子值
                    print('计算分母为' + str(moleculelist[molecule_number]) +'项的分子：limit——>' + str(limit_value), y)
                    print('计算得：', value)
            else:
                y = Y.replace('*' + moleculelist[molecule_number] + '**' + pow, '')     # 得到用来计算 该项分子值 的多项式
                limit_value = -int(re.findall('(\d+)', moleculelist[molecule_number])[0])       # 获取求极限时的 极限参数
                value = sp.limit(y, s, limit_value)         # 求极限计算 该项分子值
                print('计算分母为' + str(moleculelist[molecule_number]) + '**' + pow + '项的分子：limit——>' + str(limit_value), y)
                print('计算得：', value)

                y_diff = sp.together(sp.diff(y, s, int(pow)-1))      # 求解 除n次幂项外分式 n阶导数
                limit_value = -int(re.findall('(\d+)', moleculelist[molecule_number])[0])       # 获取求极限时的 极限参数
                value = sp.limit(y_diff, s, limit_value)        # 求极限计算 该项分子值
                print('计算分母为' + str(moleculelist[molecule_number]) + '项的'+ str(int(pow)-1) + '阶导数的分子：limit——>' + str(limit_value), y_diff)
                print('计算得：', value)

    except: pass
    molecule_number += 1

# print(molecule+'\n'+molecule)
print('分解结果为：',sp.apart(Y, s))      # 拆分结果

运行结果

运行代码，首先以例示形式输入待分解多项式，得到分解过程及结果

感悟与不足

本来打算纯手写一个留数定理分解分式多项式的程序，但是由于其中涉及到极限与微分的计算，而这两个模块编写起来又要一定时间，于是借助了sympy模块辅助编程，但是我意外地发现，sympy模块居然自带多项式分解函数 sympy.apart()因此我也在呈现分解结果时用到了这个函数，免去了字符串处理当中的一系列麻烦。因此如果大家对多项式分解的过程不在意，只想得到分解结果，只需执行sympy.apart()函数即可，至于它其中的运算原理我也不得而知。