在拙作《机器学习数学基础》中,对于机器学习直接相关的线性代数的内容做了比较详细的讲解,但是,由于书中是以“机器学习”为核心,而非“线性代数”,所以对其中的更基本的内容没有深入探究。为了让有兴趣深入学习的读者对线性代数“更上层楼”,此处再补充线性代数的基本定理。
线性代数的核心问题是向量空间的线性变换,向量空间是线性代数的研究对象,线性变换是研究向量空间的基本方法。线性变换将一个向量空间的子空间映射到另一个向量空间中的子空间。
Gilbert Strang在著作《The Fundamental Theorem of Linear Algebra》中提出线性代数有四个基本定理。本文的秩-零化度定理是其中的第一个。
以下关于秩-零化度定理(rank-nullity theorem)的阐述。以下内容主要参考文献 [2]。
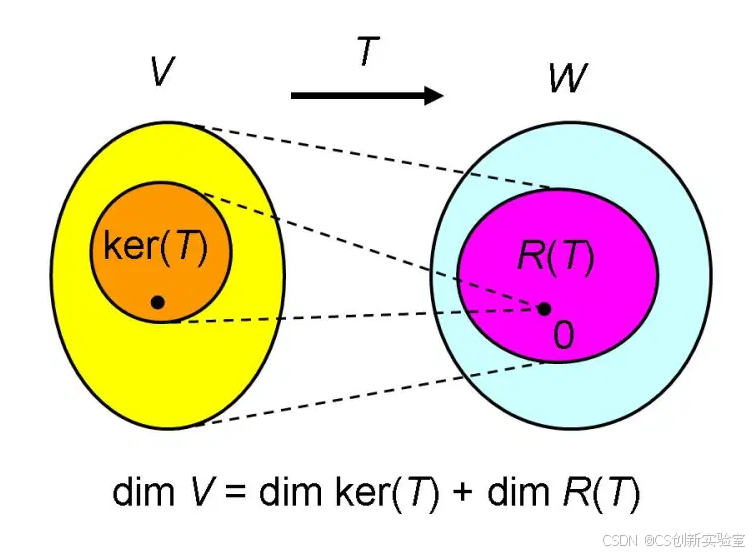
如下图所示,线性变换
T
:
V
→
W
\pmb{T}:\mathbb{V}\to\mathbb{W}
T:V→W ,
V
\mathbb{V}
V 是有限维向量空间,称为定义域;
T
\pmb{T}
T 的值域,记作:
R
(
T
)
R(\pmb{T})
R(T) ,是
W
\mathbb{W}
W 的子集,
R
(
T
)
=
{
T
(
v
)
∣
v
∈
V
}
R({\pmb{T}})=\{\pmb{T}(\pmb{v})|\pmb{v}\in\mathbb{V}\}
R(T)={T(v)∣v∈V}
-
核:若 V \mathbb{V} V 里面有一个向量集合,其中每个向量 u \pmb{u} u 经 T \pmb{T} T 映射之后为零向量,即 T ( u ) = 0 \pmb{T}(\pmb{u})=\pmb{0} T(u)=0 ,则此向量集合称为 T \pmb{T} T 的核(kernel),记作: ker ( T ) \ker(\pmb{T}) ker(T) 。 ker ( T ) \text{ker}(\pmb{T}) ker(T) 满足向量加法和数量乘法封闭性,是 V \mathbb{V} V 的一个子空间。核也称为零空间(nullspace), ker ( T ) = { v ∈ V ∣ T ( v ) = 0 } \ker(\pmb{T})=\{\pmb{v}\in\mathbb{V}|\pmb{T}(\pmb{v})=\pmb{0}\} ker(T)={v∈V∣T(v)=0} 。
-
零化度:核的维度(dimension),称为零化度(nullity),记作: dim ker ( T ) \dim\ker(\pmb{T}) dimker(T) 。可以度量核的大小。
-
秩:线性变换 T \pmb{T} T 的值域的维度,称为秩(rank),记作: rank T = dim R ( T ) \text{rank}\pmb{T}=\dim R(\pmb{T}) rankT=dimR(T) 。
秩—零化度定理
dim V = dim ker ( T ) + rank T \dim\mathbb{V}=\dim\ker(\pmb{T})+\text{rank}\pmb{T} dimV=dimker(T)+rankT
其中: dim V \dim\mathbb{V} dimV 是线性变换 T \pmb{T} T 的定义域、向量空间 V \mathbb{V} V 的维度; dim ker ( T ) \dim\ker(\pmb{T}) dimker(T) 是核的维度,即零化度; rank T \text{rank}\pmb{T} rankT 是值域的维度,即秩。
证明
证明1:通过矩阵
将线性变换 T : V → W \pmb{T}:\mathbb{V}\to\mathbb{W} T:V→W 用 m × n m\times n m×n 的矩阵 A \pmb{A} A 表示,其中: n = dim V , m = dim W n = \dim\mathbb{V}, m=\dim\mathbb{W} n=dimV,m=dimW 。
线性变换 T \pmb{T} T 的核 ker ( T ) \ker(\pmb{T}) ker(T) 即为矩阵的零空间(null space) N ( A ) N(\pmb{A}) N(A) ,它的维度即矩阵的零化度,记作 dim N ( A ) \dim N(\pmb{A}) dimN(A) 。关于零空间的详细内容,请阅读参考资料 [4]。
值域 R ( T ) R(\pmb{T}) R(T) 即为矩阵的列空间(column space) C ( A ) C(\pmb{A}) C(A) 。
将矩阵 A \pmb{A} A 化简为行梯形形式,用分块矩阵表示为:
R
=
[
I
r
F
0
0
]
\pmb{R}=\begin{bmatrix}\pmb{I}_r&\pmb{F}\\\pmb{0}&\pmb{0}\end{bmatrix}
R=[Ir0F0]
其中
R
\pmb{R}
R 的秩
r
=
rank
R
r=\text{rank}\pmb{R}
r=rankR ,
F
\pmb{F}
F 是
r
×
(
n
−
r
)
r\times(n-r)
r×(n−r) 阶矩阵。
因为矩阵行运算不改变轴数量,也不改变零空间,所以: rank A = rank R = r \text{rank}\pmb{A}=\text{rank}\pmb{R}=r rankA=rankR=r 且 N ( A ) = N ( R ) N(\pmb{A})=N(\pmb{R}) N(A)=N(R) 。
根据 R \pmb{R} R 的形状,写出 n × ( n − r ) n\times(n-r) n×(n−r) 阶零空间矩阵 P \pmb{P} P :
P
=
[
−
F
I
n
−
r
]
\pmb{P} = \begin{bmatrix}-\pmb{F}\\\pmb{I}_{n-r}\end{bmatrix}
P=[−FIn−r]
用上述结果可以计算得到
R
P
=
0
\pmb{RP}=0
RP=0 ,故确认
P
\pmb{P}
P 是零空间矩阵。
R
P
=
[
I
r
F
0
0
]
[
−
F
I
n
−
r
]
=
[
−
F
+
F
0
+
0
]
=
0
\pmb{RP}=\begin{bmatrix}\pmb{I}_r&\pmb{F}\\\pmb{0}&\pmb{0}\end{bmatrix}\begin{bmatrix}-\pmb{F}\\\pmb{I}_{n-r}\end{bmatrix}=\begin{bmatrix}-\pmb{F}+\pmb{F}\\\pmb{0}+\pmb{0}\end{bmatrix}=0
RP=[Ir0F0][−FIn−r]=[−F+F0+0]=0
设
x
=
[
x
1
x
2
]
\pmb{x}=\begin{bmatrix}\pmb{x}_1\\\pmb{x}_2\end{bmatrix}
x=[x1x2] ,其中
x
1
\pmb{x}_1
x1 是
r
r
r 维向量,
x
2
\pmb{x}_2
x2 是
n
−
r
n-r
n−r 维向量,欲使
R
x
=
0
\pmb{Rx}=\pmb{0}
Rx=0 成立,即:
R
x
=
[
I
r
F
0
0
]
[
x
1
x
2
]
=
[
x
1
+
F
x
2
0
]
=
0
\pmb{Rx}=\begin{bmatrix}\pmb{I}_r&\pmb{F}\\\pmb{0}&\pmb{0}\end{bmatrix}\begin{bmatrix}\pmb{x}_1\\\pmb{x}_2\end{bmatrix}=\begin{bmatrix}\pmb{x}_1+\pmb{Fx}_2\\\pmb{0}\end{bmatrix}=\pmb{0}
Rx=[Ir0F0][x1x2]=[x1+Fx20]=0
所以:
x
1
=
−
F
x
2
\pmb{x}_1=-\pmb{Fx}_2
x1=−Fx2 ,
于是: x = [ − F x 2 x 2 ] = [ − F I n − r ] x 2 = P x 2 \pmb{x}=\begin{bmatrix}-\pmb{Fx}_2\\\pmb{x}_2\end{bmatrix}=\begin{bmatrix}-\pmb{F}\\\pmb{I}_{n-r}\end{bmatrix}\pmb{x}_2=\pmb{Px}_2 x=[−Fx2x2]=[−FIn−r]x2=Px2
所以: C ( P ) = N ( R ) C(\pmb{P})=N(\pmb{R}) C(P)=N(R)
即: dim N ( R ) = dim C ( P ) = n − r \dim N(\pmb{R})=\dim C(\pmb{P})=n-r dimN(R)=dimC(P)=n−r 。从而证明:
n
=
dim
N
(
A
)
+
rank
A
n = \dim N(\pmb{A}) + \text{rank}\pmb{A}
n=dimN(A)+rankA
m
×
n
m\times n
m×n 的矩阵
A
\pmb{A}
A 的秩
rank
A
\text{rank}\pmb{A}
rankA 和零化度
dim
N
(
A
)
\dim N(\pmb{A})
dimN(A) 之和等于
n
n
n
证明2:线性变换的向量空间分析
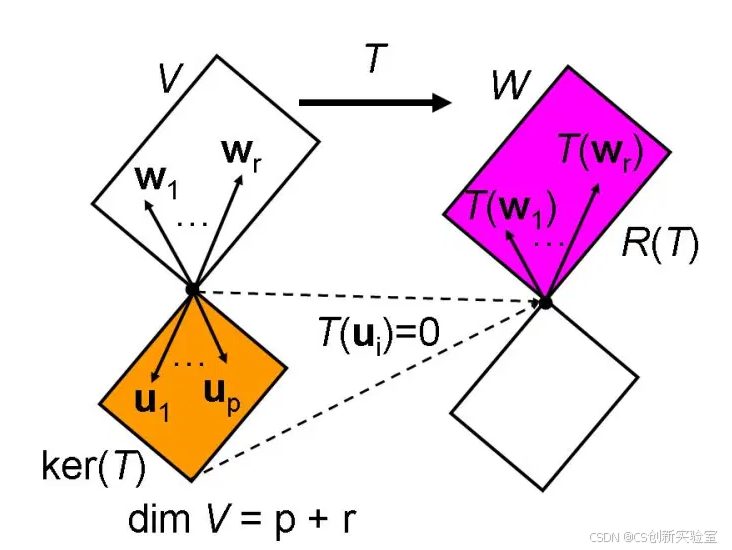
令 dim V = n , dim ker ( T ) = p , p ≤ n \dim\mathbb{V} = n,\dim\ker(\pmb{T})=p,p\le n dimV=n,dimker(T)=p,p≤n 。
设 ker ( T ) \ker(\pmb{T}) ker(T) 的一组基底为 { u 1 , ⋯ , u p } \{\pmb{u}_1,\cdots,\pmb{u}_p\} {u1,⋯,up} ,扩充此基底为向量空间 V \mathbb{V} V 的基底 { u 1 , ⋯ , u p , w 1 , ⋯ , w r } \{\pmb{u}_1,\cdots,\pmb{u}_p,\pmb{w}_1,\cdots,\pmb{w}_r\} {u1,⋯,up,w1,⋯,wr} 且 n = p + r n=p+r n=p+r。
向量空间 V \mathbb{V} V 中任一向量 v \pmb{v} v 可表示为基底向量的唯一线性组合:
v
=
a
1
u
1
+
⋯
+
a
p
u
p
+
b
1
w
1
+
⋯
+
b
r
w
r
\pmb{v}=a_1\pmb{u}_1+\cdots+a_p\pmb{u}_p+b_1\pmb{w}_1+\cdots+b_r\pmb{w}_r
v=a1u1+⋯+apup+b1w1+⋯+brwr
因为
T
(
u
)
=
0
\pmb{T}(\pmb{u})=\pmb0
T(u)=0 ,即
T
(
u
1
)
=
⋯
=
T
(
u
p
)
=
0
\pmb{T}(\pmb{u}_1)=\cdots=\pmb{T}(\pmb{u}_p)=\pmb0
T(u1)=⋯=T(up)=0 (如下图所示)
所以:
T
(
v
)
=
T
(
a
1
u
1
+
⋯
+
a
p
u
p
+
b
1
w
1
+
⋯
+
b
r
w
r
)
=
a
1
T
(
u
1
)
+
⋯
+
a
p
T
(
u
p
)
+
b
1
T
(
w
1
)
+
⋯
+
b
r
T
(
w
r
)
=
b
1
T
(
w
1
)
+
⋯
+
b
r
T
(
w
r
)
\begin{split}\pmb{T}(\pmb{v})&=\pmb{T}(a_1\pmb{u}_1+\cdots+a_p\pmb{u}_p+b_1\pmb{w}_1+\cdots+b_r\pmb{w}_r)\\&=a_1\pmb{T}(\pmb{u}_1)+\cdots+a_p\pmb{T}(\pmb{u}_p)+b_1\pmb{T}(\pmb{w}_1)+\cdots+b_r\pmb{T}(\pmb{w}_r)\\&=b_1\pmb{T}(\pmb{w}_1)+\cdots+b_r\pmb{T}(\pmb{w}_r)\end{split}
T(v)=T(a1u1+⋯+apup+b1w1+⋯+brwr)=a1T(u1)+⋯+apT(up)+b1T(w1)+⋯+brT(wr)=b1T(w1)+⋯+brT(wr)
T
(
w
1
)
,
⋯
,
T
(
w
r
)
\pmb{T}(\pmb{w}_1),\cdots,\pmb{T}(\pmb{w}_r)
T(w1),⋯,T(wr) 张成了值域空间
R
(
T
)
R(\pmb{T})
R(T) 。
设: c 1 T ( w 1 ) + ⋯ + c r T ( w r ) = 0 c_1\pmb{T}(\pmb{w}_1)+\cdots+c_r\pmb{T}(\pmb{w}_r)=0 c1T(w1)+⋯+crT(wr)=0 ,也可以写成: T ( c 1 w 1 + ⋯ + c r w r ) = 0 \pmb{T}(c_1\pmb{w}_1+\cdots+c_r\pmb{w}_r)=0 T(c1w1+⋯+crwr)=0 ,所以 c 1 w 1 + ⋯ + c r w r c_1\pmb{w}_1+\cdots+c_r\pmb{w}_r c1w1+⋯+crwr 属于零空间 ker ( T ) \ker(\pmb{T}) ker(T) 。
因为 { u 1 , ⋯ , u p } \{\pmb{u}_1,\cdots,\pmb{u}_p\} {u1,⋯,up} 是 ker ( T ) \ker(\pmb{T}) ker(T) 的基底,故可以有如下表达式:
c
1
w
1
+
⋯
+
c
r
w
r
=
d
1
u
1
+
⋯
+
d
p
u
p
c_1\pmb{w}_1+\cdots+c_r\pmb{w}_r=d_1\pmb{u}_1+\cdots+d_p\pmb{u}_p
c1w1+⋯+crwr=d1u1+⋯+dpup
又因为
{
u
1
,
⋯
,
u
p
,
w
1
,
⋯
,
w
r
}
\{\pmb{u}_1,\cdots,\pmb{u}_p,\pmb{w}_1,\cdots,\pmb{w}_r\}
{u1,⋯,up,w1,⋯,wr} 是
V
\mathbb{V}
V 的基,也就是各个向量之间线性无关,所以上式中的系数都是
0
0
0 。
故 T ( w 1 ) , ⋯ , T ( w r ) \pmb{T}(\pmb{w}_1),\cdots,\pmb{T}(\pmb{w}_r) T(w1),⋯,T(wr) 是线性无关的向量集合,是 rank ( T ) \text{rank}(\pmb{T}) rank(T) 的基。
所以: r = dim R ( T ) = rank T r=\dim R(\pmb{T})=\text{rank}\pmb{T} r=dimR(T)=rankT
由 n = p + r n=p+r n=p+r 以及前面的假设,可得:
dim V = dim ker ( T ) + rank T \dim\mathbb{V}=\dim\ker(\pmb{T})+\text{rank}\pmb{T} dimV=dimker(T)+rankT
推论
-
若 dim V > dim W \dim\mathbb{V}\gt\dim\mathbb{W} dimV>dimW ,则:
dim ker ( T ) = dim V − dim R ( T ) ≥ dim V − dim W > 0 \dim\ker(\pmb{T})=\dim\mathbb{V}-\dim R(\pmb{T})\ge\dim\mathbb{V}-\dim\mathbb{W}\gt0 dimker(T)=dimV−dimR(T)≥dimV−dimW>0
即存在非零向量 x ∈ V \pmb{x}\in\mathbb{V} x∈V 使得 T ( x ) = 0 \pmb{T}(\pmb{x})=\pmb{0} T(x)=0 ,或曰 T \pmb{T} T 不是一对一(因为 T ( 0 ) = 0 \pmb{T}(\pmb{0})=\pmb{0} T(0)=0 )。 -
若 dim V < dim W \dim\mathbb{V}\lt\dim\mathbb{W} dimV<dimW ,则:
dim R ( T ) = dim V − dim ker ( T ) ≤ dim V < dim W \dim R(\pmb{T})=\dim\mathbb{V}-\dim\ker(\pmb{T})\le\dim\mathbb{V}\lt\dim\mathbb{W} dimR(T)=dimV−dimker(T)≤dimV<dimW
即存在非零向量 y ∈ W y\in\mathbb{W} y∈W 使得 y ∉ R ( T ) \pmb{y}\notin R(\pmb{T}) y∈/R(T) ,或曰 T \pmb{T} T 不是满射。
如果用矩阵表述:将线性变换 T : V → W \pmb{T}:\mathbb{V}\to\mathbb{W} T:V→W 用 m × n m\times n m×n 的矩阵 A \pmb{A} A 表示,其中: n = dim V , m = dim W n = \dim\mathbb{V}, m=\dim\mathbb{W} n=dimV,m=dimW 。
- n > m n\gt m n>m ,则: dim N ( A ) = n − dim C ( A ) ≥ n − m > 0 \dim N(\pmb{A})=n-\dim C(\pmb{A})\ge n-m \gt 0 dimN(A)=n−dimC(A)≥n−m>0 。即零空间 N ( A ) N(\pmb{A}) N(A) 包含非零向量,或者说 A x = 0 \pmb{Ax}=0 Ax=0 有无穷多组解。
- n < m n\lt m n<m ,则: dim C ( A ) = n − dim N ( A ) ≤ n < m \dim C(\pmb{A})=n-\dim N(\pmb{A})\le n \lt m dimC(A)=n−dimN(A)≤n<m 。即列空间 C ( A ) C(\pmb{A}) C(A) 未能充满整个 R m \mathbb{R}^m Rm (或 C m \mathbb{C}^m Cm),或者说 A x = b \pmb{Ax}=\pmb{b} Ax=b 不总是有解。
进一步理解
此定理说明了线性变换前后的空间维数变化。变换后的空间维数如果相对变换前的空间维数减少了——不可能增加,说明变换前的空间经过变换之后出现了“零输出”,零空间 ker ( T ) ∈ V \ker(\pmb{T})\in\mathbb{V} ker(T)∈V 就是产生“零输出”(即零向量)的变换前的向量集合。
“秩—零化度定理”即“维数守恒定律”,
变换前的空间维数 = 零空间的维数 + 变换后的空间维数
参考文献
[1]. Gilbert Strang, The Fundamental Theorem of Linear Algebra, American Mathematical Monthly, 100, 1993, 848-855.
[2]. https://ccjou.wordpress.com/2009/03/23/線性代數基本定理-一
[3]. https://zh.wikipedia.org/wiki/秩-零化度定理