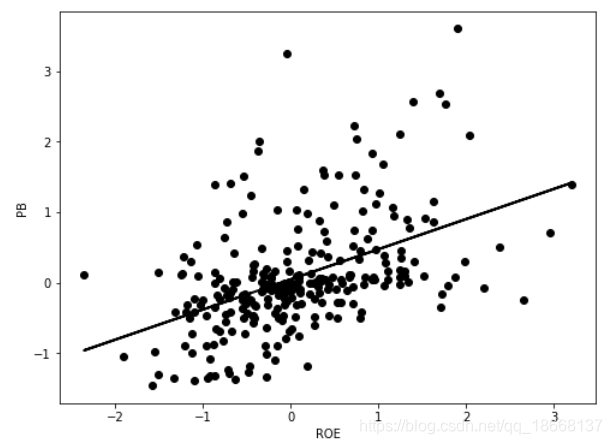
PB-ROE提供了一种投资的框架,这种框架是说,股票的PB和ROE之间存在近似的线性关系,ROE越高,PB越高,因此如果同时根据PB、ROE值来投资,很难选到同时满足PB最小、ROE最大的股票。但可以根据他们的线性关系进行选择,回归直线上的点可以视为合理的PB、ROE组合水平,这样位于回归线下方的股票都是PB被低估的,未来有很大的上升修复空间,而位于回归线上方的股票都是当前PB被高估的,未来会下降,因此投资可以选择位于回归线下方的股票。
使用这种方法最重要的点是回归必须是靠谱的,比如ROE应该是稳定的,确保未来可持续,比如应想办法消除行业间的差异等等。
import numpy as np
from atrader import *
import pandas as pd
set_setting('ALLOW_CONSOLE_SYSTEM_WARN', False)
import statsmodels.api as sm
#获取沪深300的成分股代码
get_code_list('hs300')
#获取PB,ROE数据
import atrader as at
dfData=get_factor_by_day(factor_list=['PB','ROE'], target_list=list(get_code_list('hs300').code), date='2019-08-30').set_index('code')
dfData# MAD:中位数去极值
def extreme_MAD(dt,n):
median = dt.quantile(0.5) # 找出中位数
new_median = (abs((dt - median)).quantile(0.5)) # 偏差值的中位数
dt_up = median + n*new_median # 上限
dt_down = median - n*new_median # 下限
return dt.clip(dt_down, dt_up, axis=1) # 超出上下限的值,赋值为上下限
# Z值标准化
def standardize_z(dt):
mean = dt.mean() # 截面数据均值
std = dt.std() # 截面数据标准差
return (dt - mean)/std
# 行业中性化
shenwan_industry = {
'SWNLMY1':'sse.801010',
'SWCJ1':'sse.801020',
'SWHG1':'sse.801030',
'SWGT1':'sse.801040',
'SWYSJS1':'sse.801050',
'SWDZ1':'sse.801080',
'SWJYDQ1':'sse.801110',
'SWSPCL1':'sse.801120',
'SWFZFZ1':'sse.801130',
'SWQGZZ1':'sse.801140',
'SWYYSW1':'sse.801150',
'SWGYSY1':'sse.801160',
'SWJTYS1':'sse.801170',
'SWFDC1':'sse.801180',
'SWSYMY1':'sse.801200',
'SWXXFW1':'sse.801210',
'SWZH1':'sse.801230',
'SWJZCL1':'sse.801710',
'SWJZZS1':'sse.801720',
'SWDQSB1':'sse.801730',
'SWGFJG1':'sse.801740',
'SWJSJ1':'sse.801750',
'SWCM1':'sse.801760',
'SWTX1':'sse.801770',
'SWYH1':'sse.801780',
'SWFYJR1':'sse.801790',
'SWQC1':'sse.801880',
'SWJXSB1':'sse.801890'
}
# 构造行业哑变量矩阵
def industry_exposure(target_idx):
# 构建DataFrame,存储行业哑变量
df = pd.DataFrame(index = [x.lower() for x in target_idx],columns = shenwan_industry.keys())
for m in df.columns: # 遍历每个行业
# 行标签集合和某个行业成分股集合的交集
temp = list(set(df.index).intersection(set(get_code_list(m).code.tolist())))
df.loc[temp, m] = 1 # 将交集的股票在这个行业中赋值为1
df = df.fillna(0)
return df # 将 NaN 赋值为0
# 需要传入单个因子值和总市值
def neutralization(factor,MktValue,industry = True):
Y = factor.fillna(0)
Y.rename(index = str.lower,inplace = True)
df = pd.DataFrame(index = Y.index, columns = Y.columns) # 构建输出矩阵
for i in range(Y.shape[1]): # 遍历每一天的截面数据
if type(MktValue) == pd.DataFrame:
lnMktValue = MktValue.iloc[:,i].apply(lambda x:math.log(x)) # 市值对数化
lnMktValue.rename(index=str.lower, inplace=True)
if industry: # 行业、市值
dummy_industry = industry_exposure(Y.index.tolist())
X = pd.concat([lnMktValue,dummy_industry],axis = 1,sort = False) # 市值与行业合并
else: # 仅市值
X = lnMktValue
elif industry: # 仅行业
dummy_industry = industry_exposure(factor.index.tolist())
X = dummy_industry
# X = sm.add_constant(X)
result = sm.OLS(Y.iloc[:,i].astype(float),X.astype(float)).fit() # 线性回归
df.iloc[:,i] = result.resid # 每日的截面数据存储到df中
return dfdfData = dfData.loc[dfData['PB']>0]
dfData = dfData.loc[dfData['PB']<10]
dfData = dfData.loc[dfData['ROE']>0]
dfData = dfData.loc[dfData['ROE']<10]
# 去极值和标准化
data_S = standardize_z(dfData)
# 行业中性化
data_S_ID_PB = neutralization(data_S[['PB']],0)
data_S_ID_ROE = neutralization(data_S[['ROE']],0)
#回归数据准备
x = data_S_ID_ROE[['ROE']]
x['Intercept'] = 1
x_ = x[['Intercept','ROE']]
y = data_S_ID_PB['PB']
#回归
model = sm.OLS(y.astype(float),x_.astype(float))
result=model.fit()
#回归系数
result.params
#answer:
#Intercept 0.04428
#ROE 0.42821
#拟合曲线
y_fitted = data_S_ID_ROE*result.params[1]+result.params[0]
df = pd.DataFrame()
df[['PB']] = data_S_ID_PB
df['ROE'] = data_S_ID_ROE
df['y_fitted'] = y_fitted
import matplotlib.pyplot as plt
plt.figure(figsize = (8,6))
plt.plot(df['ROE'], df['PB'],'ko', label='sample')
plt.plot(df['ROE'], df['y_fitted'], 'black',label='OLS',linewidth = 2)
plt.xlabel('ROE')
plt.ylabel('PB')
plt.show()df_choice = df.loc[df['PB']<df['y_fitted']]
df_choice.head()