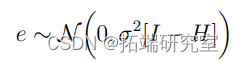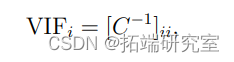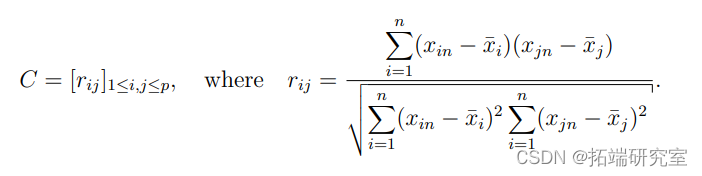最近我们被客户要求撰写关于回归的研究报告,包括一些图形和统计输出。
一些标准的图形工具可以极大地帮助理解数据集并评估所建议模型的质量。
学生考试成绩
例如,数据集包含600个观察结果,用于国家统计教育中心对学生进行的一项非常大的研究。数据集中的一些变量包括:
•性别:性别男性或女性。
•种族:种族或民族,具有西班牙裔,亚洲人,非洲裔美国人,白人的水平。
•学校类型,公立和私立。
•轨迹:控制位点,一个连续的协变量,指示受试者对影响他们的事件的自我感知控制程度(更高=更感知的控制)
•概念:自我概念,反映受试者自我感知的学术能力的连续协变量(更高=更多的自我感知能力)。
•动机,一个连续的协变量(更高=更多的自我感知的动机)。
•数学:标准化的数学考试成绩。
• 阅读:标准化阅读测试成绩。
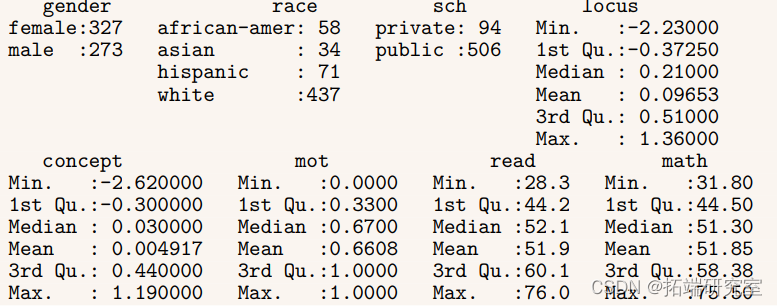
要基本了解数据集中的变量,我们可以使用摘要命令:
summary(hsb)
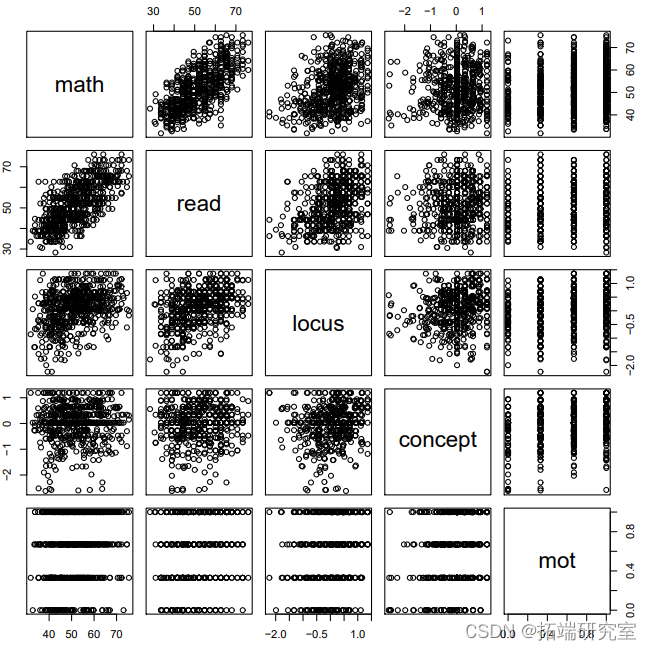
然而,由于变量太少,我们实际上可以用成对命令把所有的连续变量绘制在一起。
图中显示,虽然动机是一个连续变量,但它只具有四个类别。这很可能是因为学生被要求在4个点的量表上评估他们的自我激励(0,0.33,0.66,和1)。另外,数学和任何一个连续预测因素之间最强的关联似乎是与阅读。
anova(M1, M2)
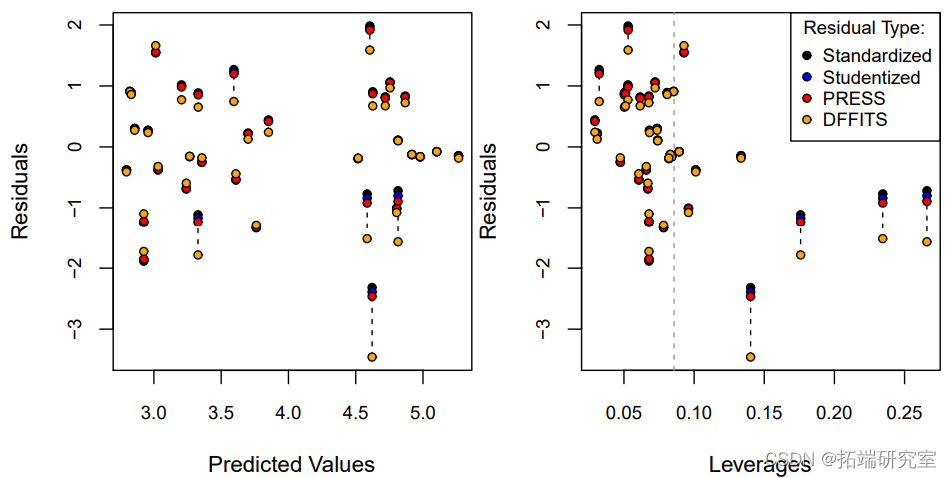
有两个标准图来检查M1是否似乎违反了线性模型的假设。第一种是绘制残差ei = yi - x ′ iβˆ作为预测值的函数ˆyi = x ′ iβˆ。除了通常的残差之外,还有两种类型的残差经常被考虑。
1. 标准化残差:ri = ei σˆ。这些残差是单位的
2. 研究性残差:di = ei σˆ √ 1 - hi
这样,如果模型是真实的,残差大约是N(0,1)。
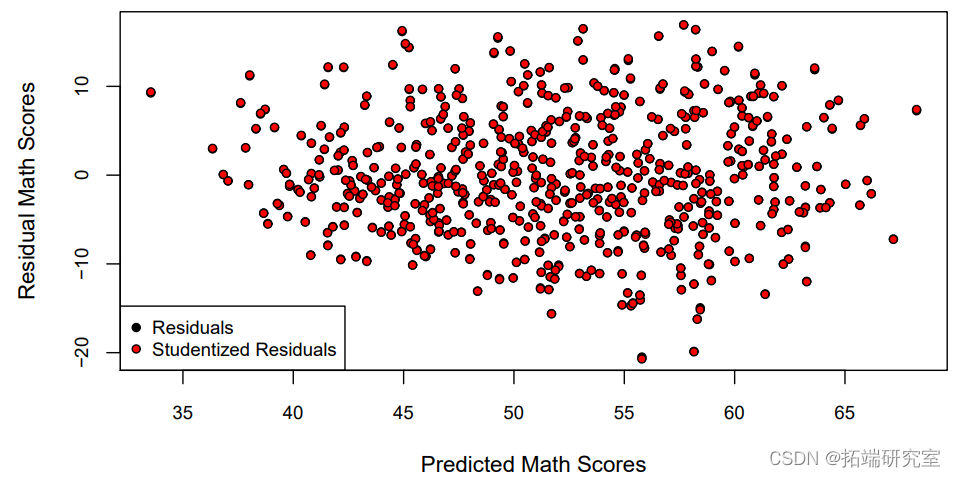
图1显示了残差与M1的拟合值之间的关系,使用的是通常的残差和 studentized残差的一个版本,ei/ √ 1 - hi 。其他统计学家更喜欢在标准化的尺度上绘制残差(除以σˆ),这样Y轴上的单位对每张残差图都有相同的解释。
plot(predict(M1), res, pch = 21, bg = "black", cex = cex, cex.axis = cex,
ex)由于σ2(1-hi)是一个方差,我们必须有(1-hi)>0=⇒hi<1=⇒(1-hi)<1。因此,studentized残差ei/ √ 1 - hi在规模上大于原始的ei。
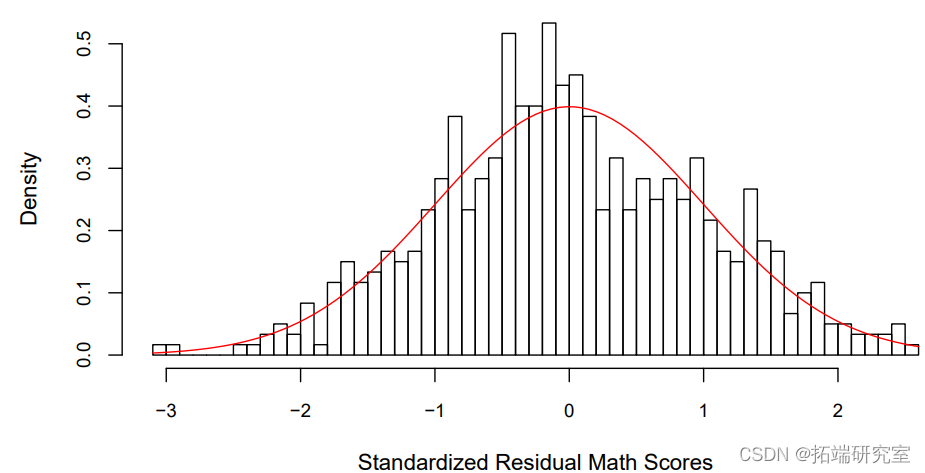
通过绘制残差与理论上的正态分布的直方图,可以更容易地看到这一点,如图所示。
hist(res/sigma.hat, breaks = 50, freq = FALSE, cex.axis = cex,
对于这个残差图,我个人更喜欢使用标准化的残差,即除以ˆσ。这是因为我更容易在N(0,1)上发现大的残差值(标准正态在±2之间有95%的机会,在±3之间有99.7%的机会)。图2证实了残差略微偏向负值,表明需要进一步建模。
线性预测模型
回顾一下满意度数据集,即病人自我报告对在医院接受的护理质量的满意度,由年龄、压力和病情的严重程度来预测。下面是潜在模型之间的一些比较。
anova(lm(Satisfaction ~ Age
anova(lm(Satisfaction ~ Age, data = satis),
anova(lm(Satisfaction ~ Age + Severity, data = satis),
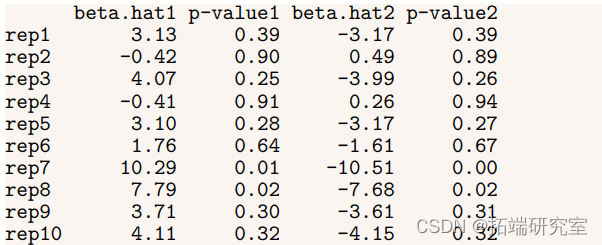
根据上面的测试结果,我们可以决定考虑使用年龄和压力的模型,因为它的F统计量比年龄和严重程度稍显重要。然而,这种方法会增加选择错误模型的机会,正如下面的模拟实验所显示的那样。
pval <- 2*pt(abs(beta.hat)/sqrt(diag(vcov(M))[-1]),
df = n-3, lower.tail = FALSE) # pvalues
sim.out[ii,] <- round(c(beta.hat[1], pval[1], beta.hat[2], pval[2]),2)
}
sim.out
在10次实验运行中,只有两次对两个协变量都有显著的P值,但对这些协变量的估计却有很大偏差。事实上,其中两个复制甚至把协变量的符号弄错了。虽然这个例子并不现实(协变量之间的相关性几乎不可能达到0.999),但它说明了这样一个事实:当协变量高度相关时,回归很难弄清y的变化是由一个协变量还是另一个协变量引起的。换句话说,βˆ的估计值从一个随机样本到另一个随机样本会有很大的变化。这种现象被称为方差膨胀
衡量预测因子之间的共线性的一个简单方法是所谓的方差膨胀因子(VIF)。
其中C是协变量之间的样本相关矩阵。
下面的R代码说明了VIF的两种形式之间的平等。
VIF <- diag(solve(cor(X)))
VIF
names(satis.star) <- c("Satisfaction", paste0(names(satis)[-1], ".star"))
head(satis.star)
diag(vcov(M.orig))["Severity"]/diag(vcov(M.trans))["Severity.star"]
VIF["Severity"]
严重程度和压力的方差膨胀系数为2.00,这两个变量之间的相关度为0.67。相比之下,模拟实验中的方差膨胀系数是1/(1-.9992)≈500。作为一条经验法则,VIF大于10是值得关注的。
离群值
简单地说,离群值是指与其他观测值相比具有异常大的残差。然而,为了提高模型的拟合度而删除这些观测值的情况比较少见,因为出错的几乎总是模型,而不是数据。也就是说,异常值通常是模型中遗漏了重要协变量的结果。例如,数据集包含了105个世界国家的婴儿死亡率和人均收入的数据。数据集中的变量是
- 收入:以元计的人均收入。
- 婴儿:每1000个活产的婴儿死亡率。
- 地区:大陆,有非洲、美洲、亚洲、欧洲等级别。
- 石油:石油出口国,级别为无、有。
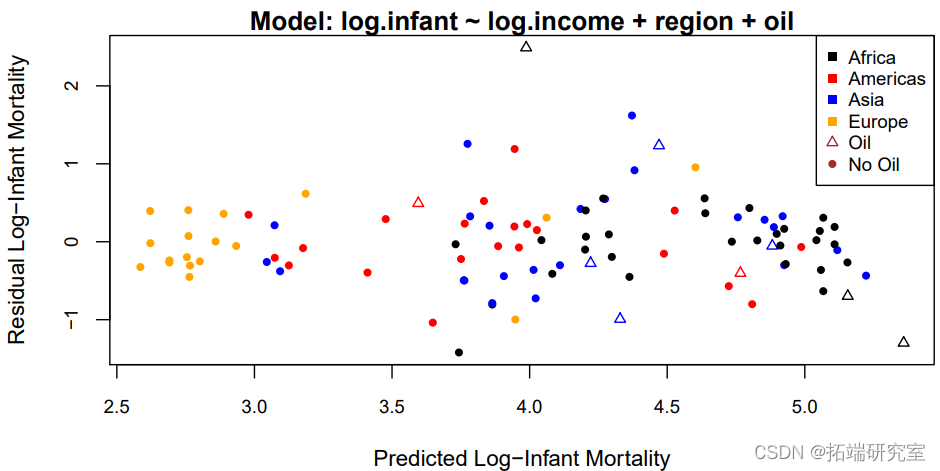
对数尺度的线性模型适合于数据,残差与拟合值绘制在图3中。
coef(M) # 系数
as.character(formula(M))[c(2,1,3)]), collapse = " "), # 模型
xlab = "Predicted Log-Infant Mortality",
这张图上的异常点是最上面的三角形,它对应的是沙特阿拉伯。目前还不清楚为什么沙特阿拉伯的婴儿死亡率比模型预测的要高很多。一种可能性是,它的石油产量太高,以至于歪曲了平均收入。在这种情况下,我们有以下选择。
1. 将沙特阿拉伯排除在分析之外,承认我们并不完全知道原因(不推荐)。
2. 将所有9个产油国排除在分析之外,并说明我们的预测只针对非产油国。
3.将沙特阿拉伯排除在外,并评估这对我们的分析有何影响。
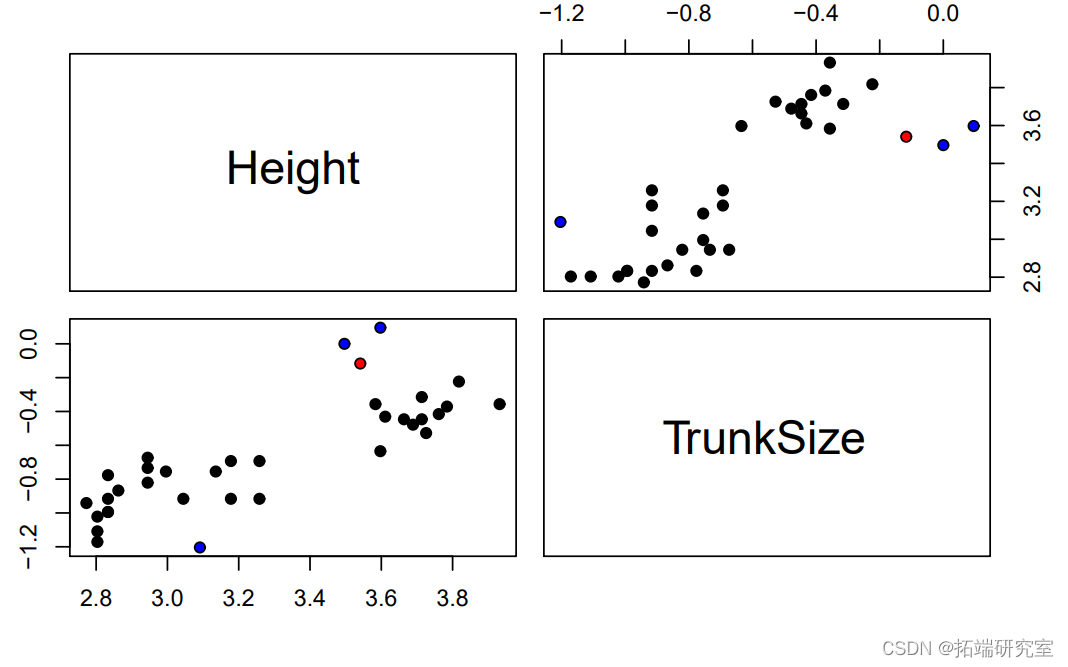
树木的针叶产生的阴凉面积
数据集包含以下关于35种针叶树的变量。- 针叶面积。树木的针叶产生的阴凉面积 - 高度:树木的高度 - 树干尺寸。树的直径 以下模型适合于该数据。
X <- model.matrix(M)
H <- X %*% solve(crossprod(X), t(X)) # HAT matrix
head(diag(H))
range(h - diag(H))
在这四种类型的残差中,每一种都把大残差放大得越来越多。为了衡量每个观测点的总体影响,图中的库克距离与杠杆率作了对比
n <- nrow(lforest)
hbar <- p/n # 平均杠杆率
abline(v = 2*hbar, col = "gray60", lty = 2) # 2x平均杠杆率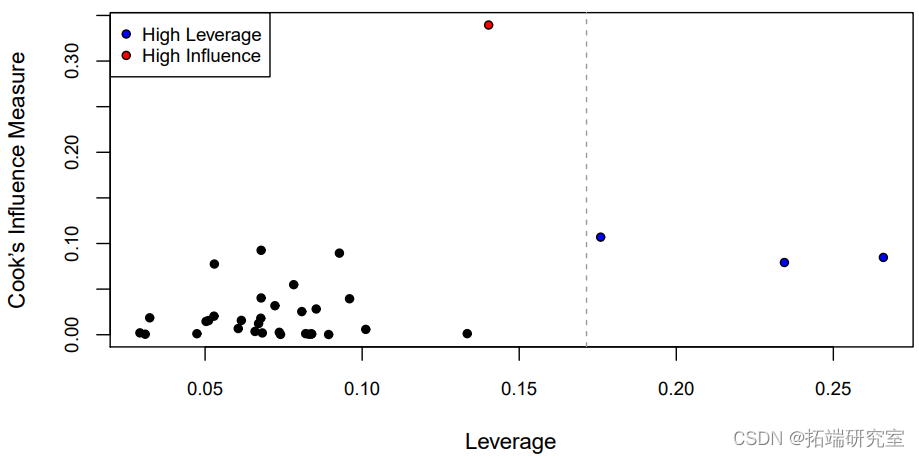
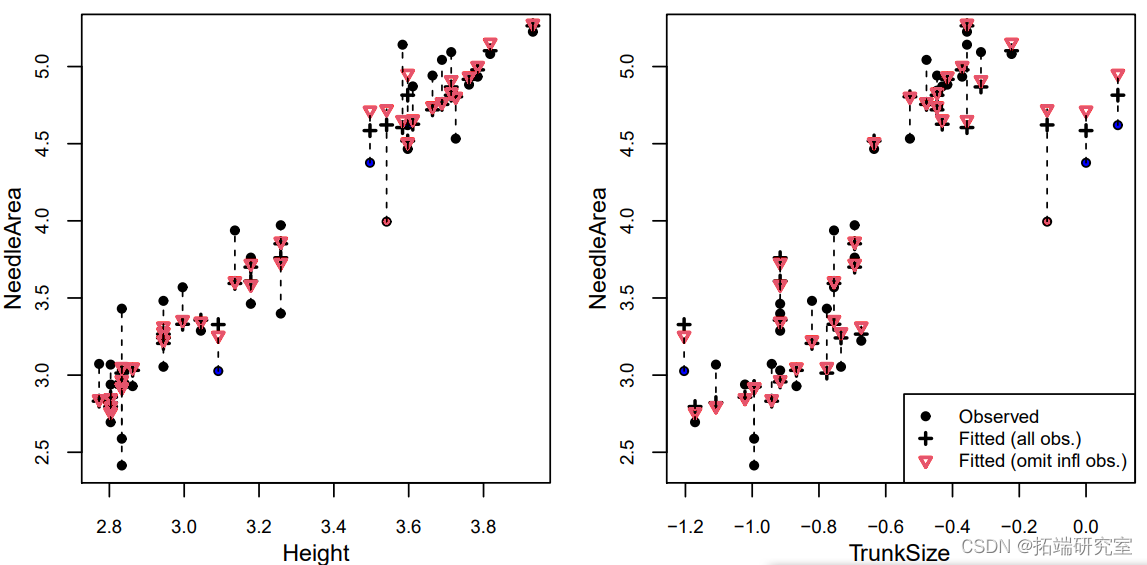
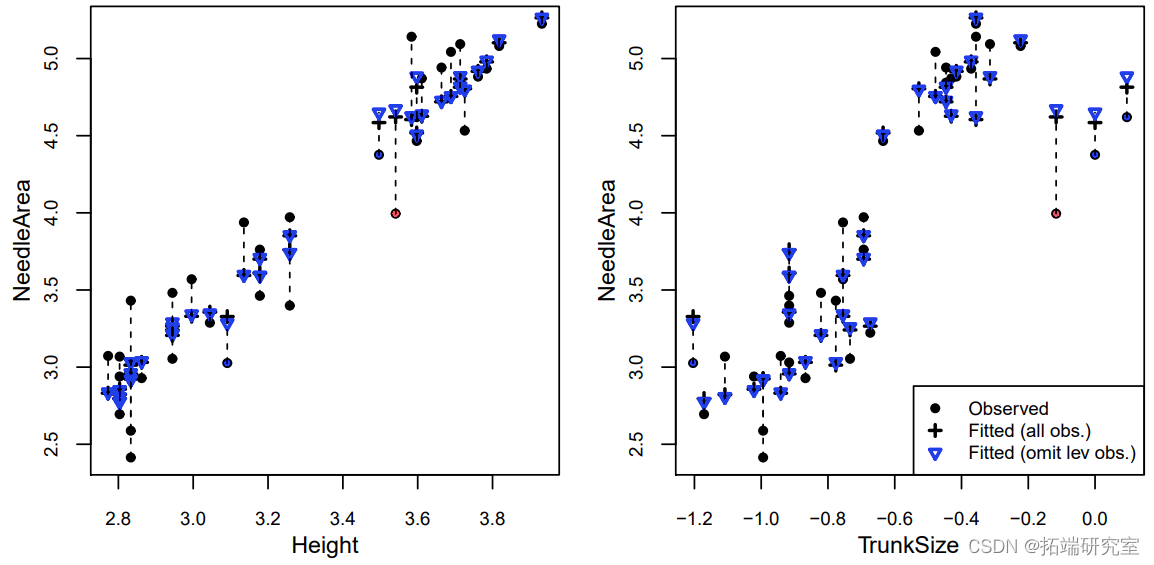
我们可以看到,其中三个标记点(有影响力的点和两个高杠杆点)的TrunkSize值非常大(记得这些值是按对数比例绘制的)。剩下的那个高杠杆点的树干尺寸相对于其高度来说非常小。至于为什么只有三棵树中树干尺寸最大的一棵被标记为离群点,我们可以将NeedleArea与每个协变量(包括实际值和预测值)作对比。为了进行比较,预测是在所有观测值和省略一个观测值的情况下进行的:要么是有影响力的观测值,要么是有最高杠杆的观测值。
# 用省略的值进行预测
omit.ind <- c(which(inf.ind), # 最有影响力的
which.max(h)) # 最高杠杆率
which(infl.ind)中的错误:"which "的参数不符合逻辑
names(omit.ind) <- c("inf", "lev")
omit.ind
yobs <- lforest[, "NeedleArea"] # 观察值
Mf <- lm(NeedleArea ~ Height + TrunkSize, data = lforest) # 所有观测值
for(jj in 1:length(opt.ind)) {
# 用省略的观察值建立模型
Mo <- lm(NeedleArea ~ Height + TrunkSize,
data = lforest, subset = -omit.ind[jj])
yfito <- predict(Mo, newdata = lforest) # 所有观测值的拟合值
for(ii in c("Height", "TrunkSize")) {
我们可以看到,当移除有影响的观测值时,有无遗漏的预测值之间的差异更加明显。这在针孔面积与树干尺寸的图中最为明显,这是对具有高杠杆作用的三个点和具有高影响的点的预测。在这个特殊的案例中,我们确定具有最大树干尺寸的三棵树的测量是不正确的,它们可以从分析中移除。