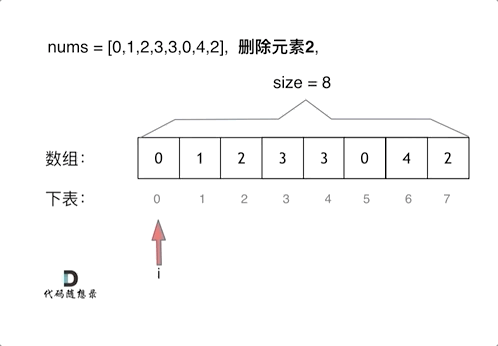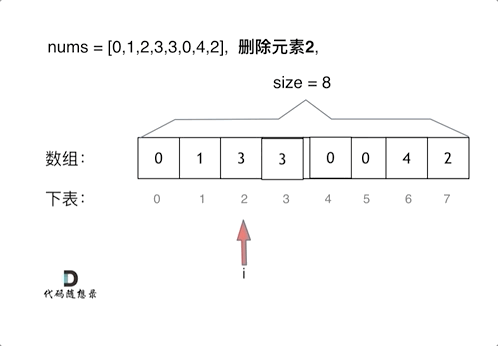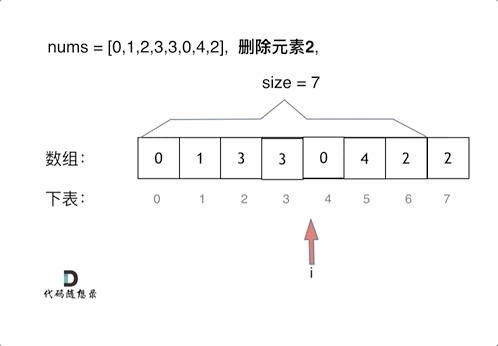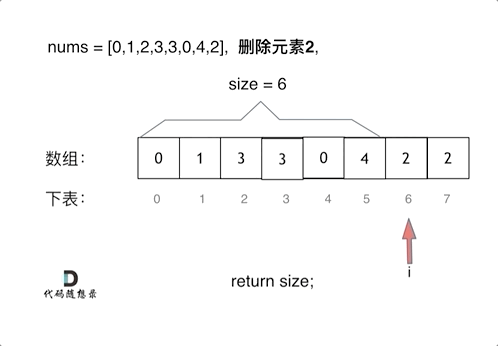
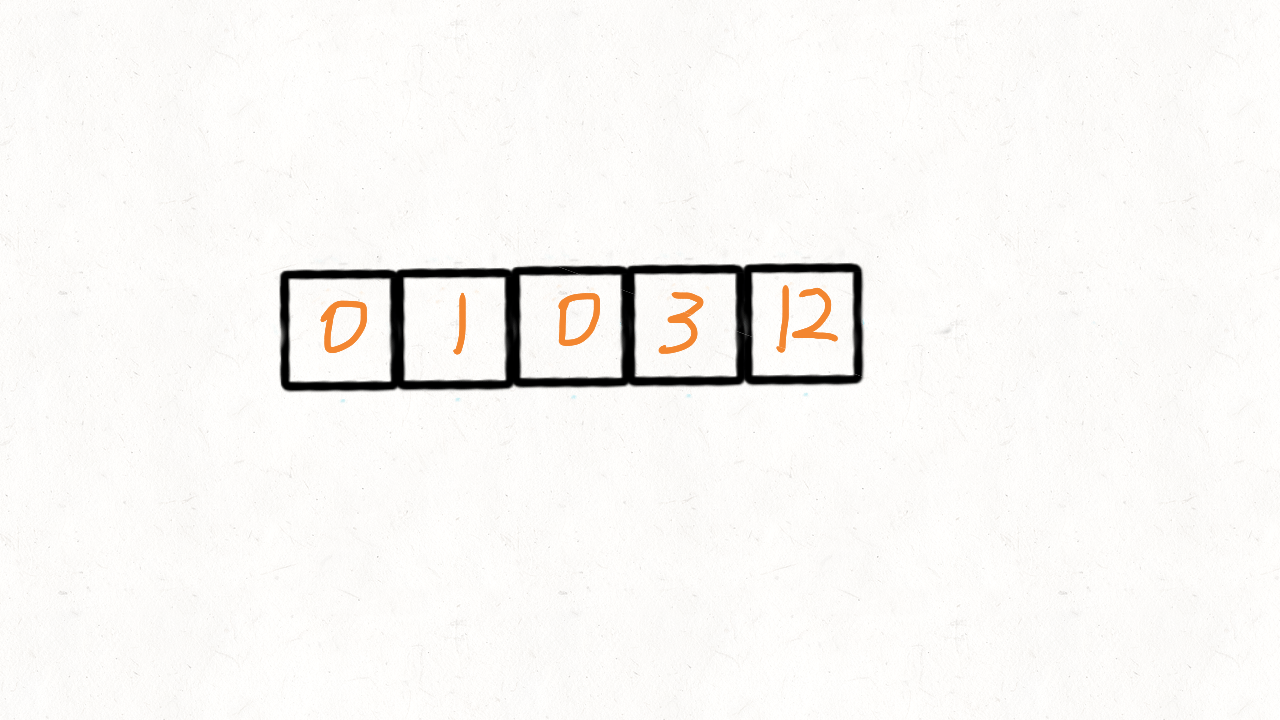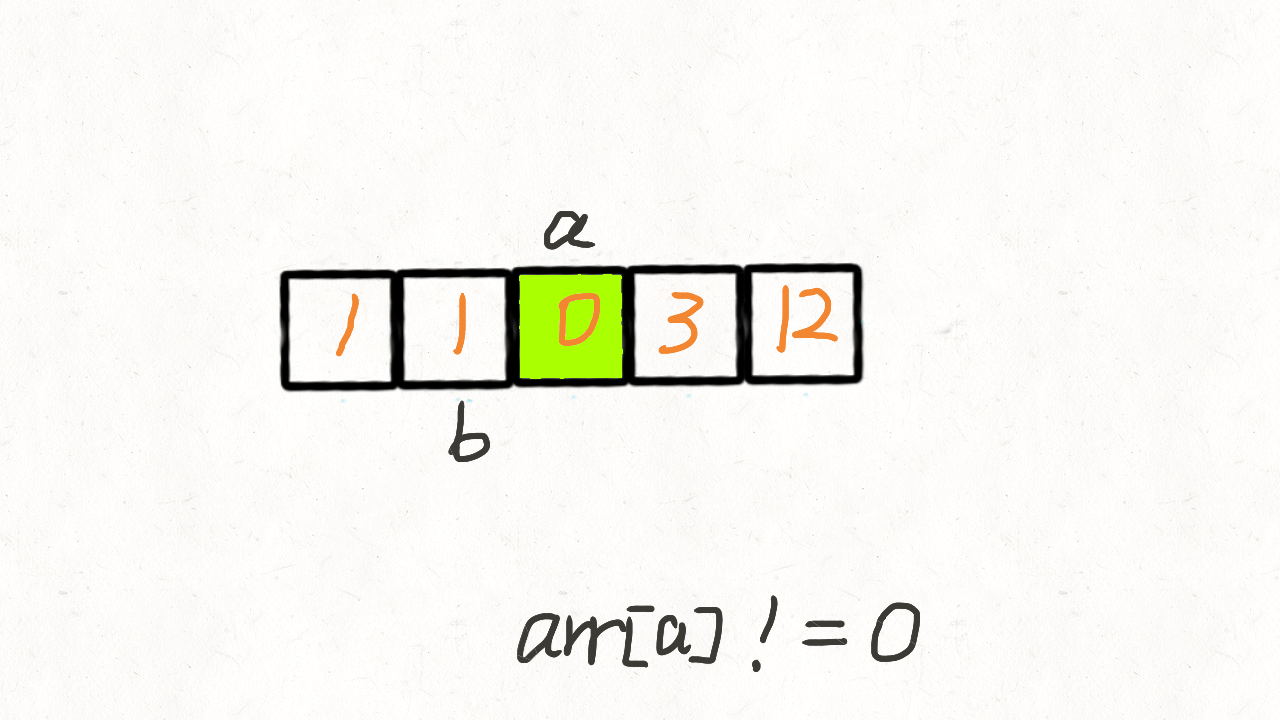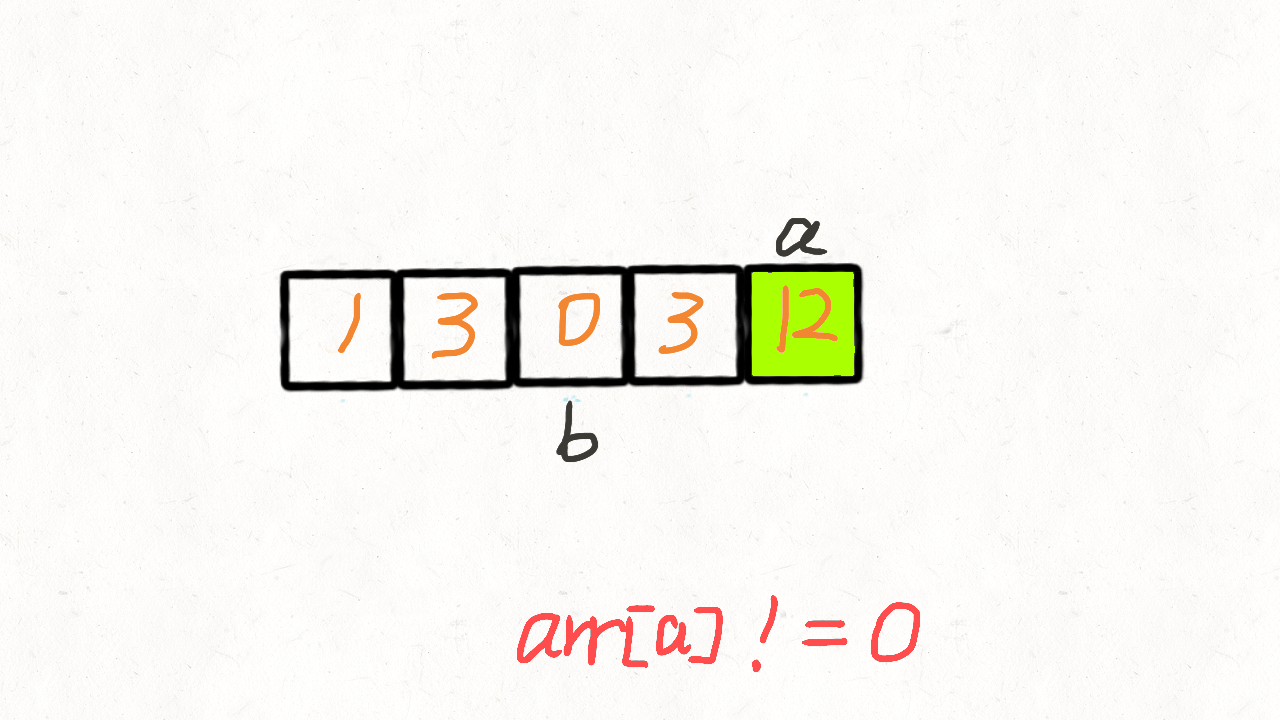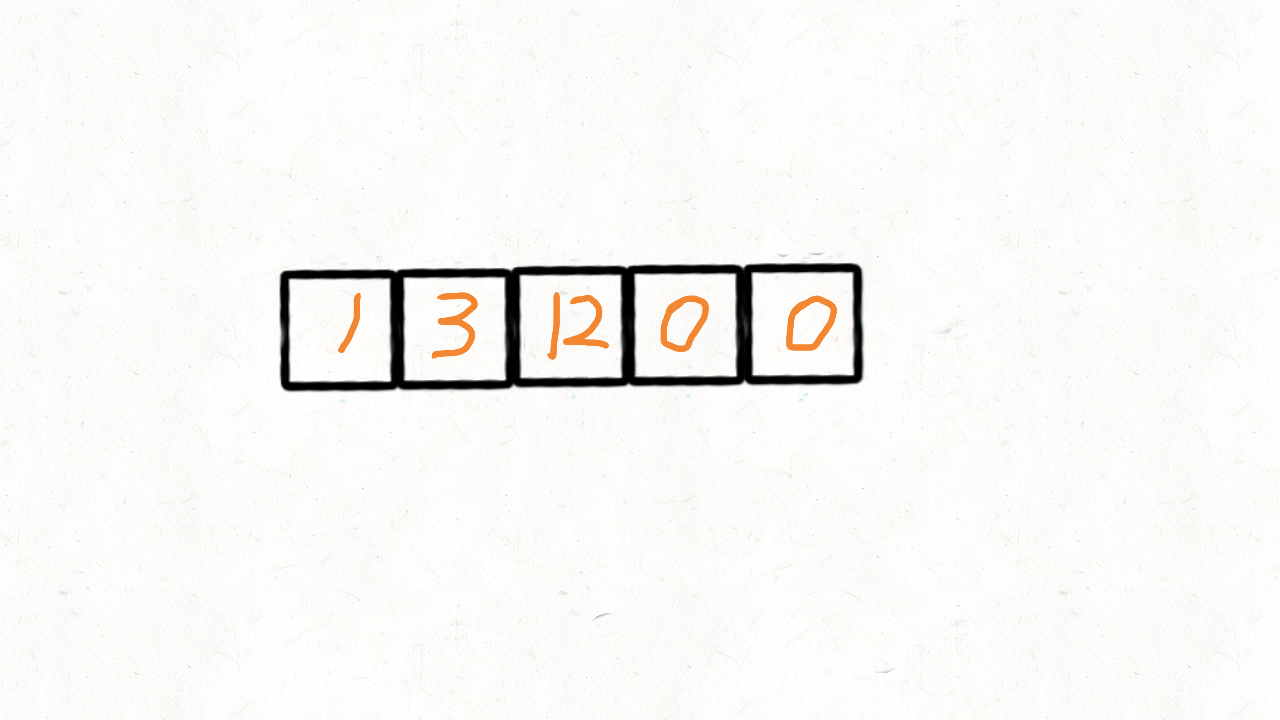C++ 数据结构与算法（二）（双指针法）

数组双指针法

27. 移除元素 ●

给定一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。

1、普通暴力解法

代码随想录图解
两层for循环，一个for循环遍历数组元素，当元素等于val时，调用第二个for循环更新数组，将之后所有元素前移（覆盖删除），时间复杂度为 $O(n^2)$ 。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        // 暴力解法
        int n = nums.size();
        for (int i = 0; i < n; i++){
            if (nums[i] == val){    // 发现需要移除的元素，就将数组集体向前移动一位
                for (int j = i + 1; j < n; j++){
                    nums[j -1] = nums[j];
                }
                i--;    // 下标i以后的数值都向前移动了一位，所以i也向前移动一位
                n--;    // 此时数组的大小-1
            }
        }
        return n;
    }
};

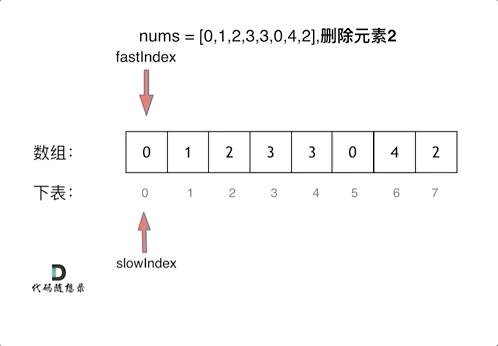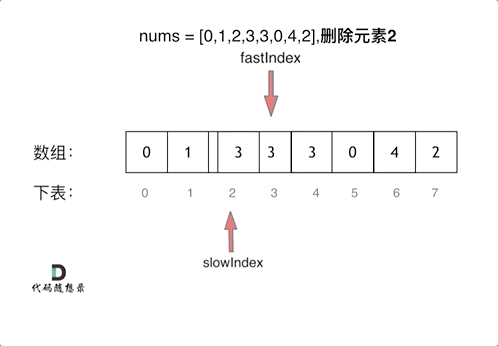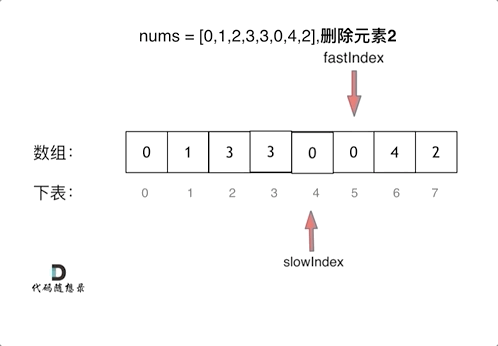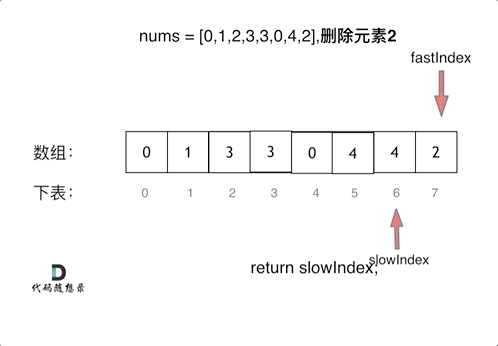
2、双指针法（快慢指针）

代码随想录图解
通过一个快指针和慢指针在一个for循环下完成两个for循环的工作,把输出的数组直接写在输入数组上。

思路：

右指针 fast 指向当前将要处理的元素，左指针 slow 指向下一个将要赋值的位置。

如果 fast 指针指向的元素不等于 val，它一定是输出数组的一个元素，我们就将 fast 指针指向的元素复制到 slow 指针位置，然后将两个指针同时右移；

如果右指针指向的元素等于 val，它不能在输出数组里，此时 slow 指针不动，fast 指针右移一位。

整个过程保持不变的性质是：区间 [0,slow) 中的元素都不等于val。当左右指针遍历完输入数组以后，slow 的值就是输出数组的长度。

这样的算法在最坏情况下（输入数组中没有元素等于 val），左右指针各遍历了数组一次。
未改变其他元素的相对顺序。

时间复杂度： $O (n)$ ，其中 n 为序列的长度，我们只需要遍历该序列至多两次。
空间复杂度： $O (1)$

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        // 双指针
        int slow = 0;
        int n = nums.size();
        for (int fast = 0; fast < n; fast++){
            if (nums[fast] != val){
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
    }
};

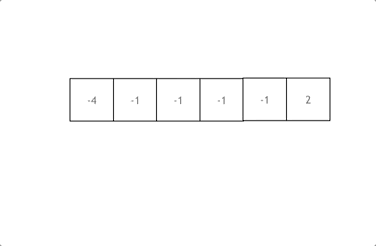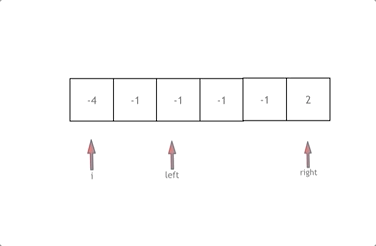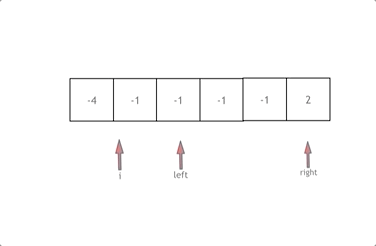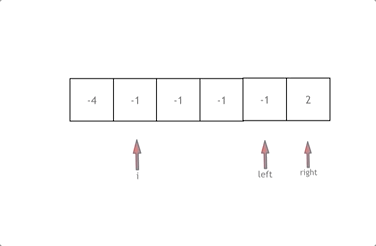
3、双指针优化（首尾）

因为题目允许改变元素原本的相对顺序，所以可以两个指针初始时分别位于数组的首尾，向中间移动遍历该序列。

如果左指针 left 指向的元素等于 val，此时将右指针 right 指向的元素复制到左指针 left 的位置，然后右指针 right 左移一位。如果赋值过来的元素恰好也等于 val，可以继续把右指针 right 指向的元素的值赋值过来（左指针 left 指向的等于 val 的元素的位置继续被覆盖），直到左指针指向的元素的值不等于 val 为止。

当左指针 left 和右指针 right 重合的时候，左右指针遍历完数组中所有的元素。

这样的方法两个指针在最坏的情况下合起来只遍历了数组一次，避免了需要保留的元素的重复赋值操作。

时间复杂度： $O (n)$ ，其中 n 为序列的长度，只需要遍历该序列至多一次。
空间复杂度： $O (1)$ ，只需要常数的空间保存若干变量。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        // 双指针优化
        int n = nums.size();
        int right = n - 1;
        for (int left = 0; left <= right; left++){
            if (nums[left] == val){
                nums[left--] = nums[right--];
                // 等价于
                // nums[left] = nums[right];
                // right--;
                // left--;
            }
        }
        return right+1;
    }
};

更好理解版本：

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int left = 0;
        int right = nums.size() - 1;
        while(left <= right){
            if(nums[left] == val && nums[right] == val){
                --right;
            }else if(nums[left] == val && nums[right] != val){
                nums[left] = nums[right];
                ++left;
                --right;
            }else if(nums[left] != val){
                ++left;
            }
        }
        return left;
    }
};

26. 删除有序数组中的重复项 ●

在升序数组中，使每个元素只出现一次，且保持升序。

由于给定的数组 nums 是有序的，因此对于任意 $i < j$ ，如果 $n u m s [i] = n u m s [j]$ ，则对任意 $i \leq k \leq j$ ，必有 $n u m s [i] = n u m s [k] = n u m s [j]$ ，即相等的元素在数组中的下标一定是连续的。利用数组有序的特点，可以通过双指针的方法删除重复元素。

时间复杂度： $O (n)$ ，其中 n 是数组的长度，快指针和慢指针最多各移动 n 次。
空间复杂度： $O (1)$ ，只需要使用常数的额外空间。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int slow = 1;
        int n = nums.size();
        for (int fast = 1; fast < n; fast++){
            if (nums[fast] != nums[slow-1]){             
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
    }
};

80. 删除有序数组中的重复项 II ●●

在升序数组中，使每个元素只出现最多两次，且保持升序。

使用双指针，遍历数组检查每一个元素是否应该被保留，如果应该被保留，就将其移动到指定位置。具体地，我们定义两个指针 slow 和 fast 分别为慢指针和快指针，其中慢指针表示处理出的数组的长度，快指针表示已经检查过的数组的长度。

检查上上个应该被保留的元素 nums[slow−2] 是否和当前待检查元素 nums[fast] 相同。当且仅当 $n u m s [s l o w - 2] = n u m s [f a s t]$ 时，当前待检查元素 nums[fast] 不应该被保留，等待 slow 指针指向该位置后被覆盖；否则当前待检查元素 nums[fast] 应当保留，并赋值到 slow 位置，slow 指针右移一位。最后，slow 即为处理好的数组的长度。

该方法可拓展到 “在升序数组中，使每个元素只出现最多 k 次，且保持升序”，此时则与 $n u m s [s l o w - k]$ 进行比较，将一下代码的“2”变为相应 $k$ 值即可。

时间复杂度： $O (n)$ ，最多遍历该数组一次。
空间复杂度： $O (1)$

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int slow = 2;
        int n = nums.size();
        if (n<=2){		// 直接保留前两位
            return n;
        }
        for (int fast = 2; fast < n; fast++){        
            if (nums[fast] != nums[slow-2]){
                nums[slow] = nums[fast];
                slow++;		// 待覆盖指针右移
            }
        }
        return slow;
    }
};

283. 移动零 ●

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意，必须在不复制数组的情况下原地对数组进行操作。

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

1、首先通过快慢指针移除数值为 0 的元素，然后从慢指针开始遍历，将末尾元素置0.

时间复杂度: $O (n)$
空间复杂度: $O (1)$

在这里插入图片描述

class Solution {
public:
	// 移动零到最末端
    void moveZeroes(vector<int>& nums) {
        int slow = 0;
        int n = nums.size();
        for (int fast = 0; fast < n; fast++){  	//第一次遍历，保留非0元素
            if (nums[fast] != 0){
                nums[slow] = nums[fast];
                slow++;
            }
        }
        for (int i = slow; i < n; i++){			//第二次不完全遍历，末尾置0
            nums[i] = 0;
        }
    }
};

2、通过双指针判断，把不为 0 的元素与 0 值替换，并移动指针。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int n = nums.size();
        int left = 0;
        for(int right = 1; right < n; ++right){
            if(nums[left] == 0 && nums[right] != 0){
                swap(nums[left++], nums[right]);
            }else if(nums[left] != 0){
                ++left;
            }
        }     
    }
};

844. 比较含退格的字符串 ●

1、双指针 - 重构字符串

利用快慢指针遍历、重写字符串，再进行比较。

时间复杂度： $O (N + M)$ ，其中 N 和 M 分别为字符串 S 和 T 的长度。我们需要遍历两字符串各一次。
空间复杂度： $O (1)$ 。

class Solution {
public:
    void rebuild (string &s){				// &引用调用，改变实际参数
        int index = 0;						// 相当于 慢指针
        for (char ch : s){					// 相当于 快指针遍历
            if (ch != '#'){                  // 非 # 为待保留文本
                s[index] = ch;               // 重写s
                index++;                    // 待覆盖指针右移
            }
            else{
                if (index > 0) index--;     // 避免对空文本退格出错的情况
            }
        }
        s.resize(index);                    // 重置字符串大小
    }

    bool backspaceCompare(string s, string t) {
        rebuild(s);
        rebuild(t);
        return s==t;
    }
};

2、栈

用栈处理遍历过程，每次我们遍历到一个字符：

如果它是退格符，那么我们将栈顶弹出； .pop_back()
如果它是普通字符，那么我们将其压入栈中。 .push_back(ch)
时间复杂度： $O (N + M)$ ，其中 N 和 M 分别为字符串 S 和 T 的长度。我们需要遍历两字符串各一次。
空间复杂度： $O (N + M)$ ，其中 N 和 M 分别为字符串 S 和 T 的长度。主要为还原出的字符串的开销。

class Solution {
public:
    string rebuild (string s){
        string temp;
        for(char ch : s){
            if(ch != '#'){
                temp.push_back(ch);    // 入栈
            }
            else if(!temp.empty()){
                temp.pop_back();       // 弹出栈顶
            }
        }
        return temp;
    }

    bool backspaceCompare(string s, string t) {
        return rebuild(s)==rebuild(t);
    }
};

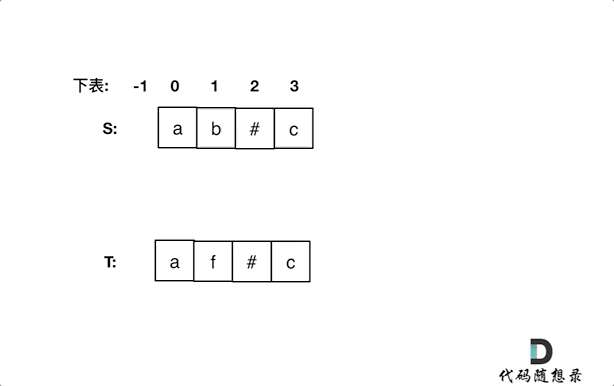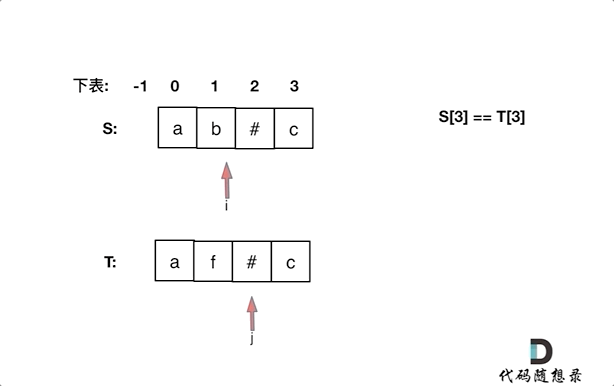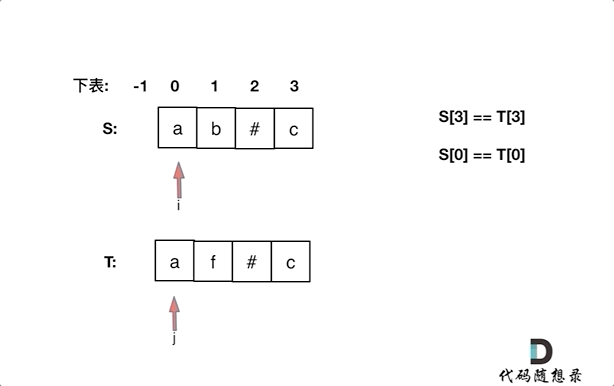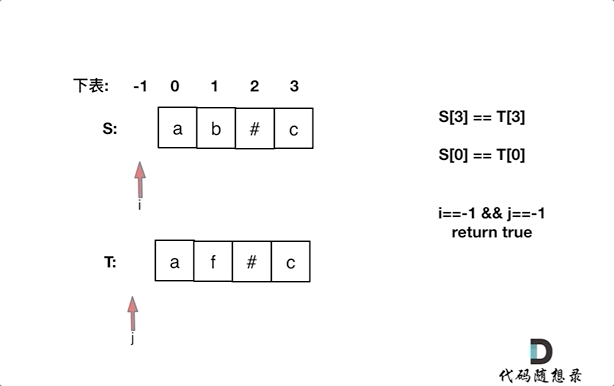
3、从后往前双指针遍历

同时从后向前遍历S和T（ i 初始为S末尾，j 初始为T末尾），记录 # 的数量，模拟消除的操作，如果 # 用完了，就转到比较S[i]和S[j]。
如果S[i]和S[j]不相同，或有一个指针（i或者j）先走到的字符串头部位置，则返回 false。

时间复杂度： $O (N + M)$ ，其中 N 和 M 分别为字符串 S 和 T 的长度。我们需要遍历两字符串各一次。
空间复杂度： $O (1)$ 。

在这里插入图片描述

class Solution {
public:
    bool backspaceCompare(string s, string t) {
        int slen = s.length(), tlen = t.length();
        int sidx = slen-1, tidx = tlen-1;
        while(sidx >= 0 || tidx >= 0){
            int cnt = 0;
            while(sidx >= 0){
                if(s[sidx] == '#'){     // 找到一个实际存在 s 的字符
                    --cnt;
                }else{
                    ++cnt;
                }
                if(cnt > 0) break;
                --sidx;
            }
            cnt = 0;
            while(tidx >= 0){
                if(t[tidx] == '#'){     // 找到一个实际存在 t 的字符
                    --cnt;
                }else{
                    ++cnt;
                }
                if(cnt > 0) break;
                --tidx;
            }
            if((sidx < 0 && tidx >= 0) ||   // 长度不一致
                (tidx < 0 && sidx >= 0) ||  // 字符不相同
                (sidx >= 0 && tidx >= 0 && s[sidx] != t[tidx])) return false;
            --tidx;     // 移动指针，找下一个字符
            --sidx;
        }
        return true;
    }
};

977. 有序数组的平方 ●

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

1、暴力排序

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        for (int i = 0; i < A.size(); i++) {
            A[i] *= A[i];
        }
        sort(A.begin(), A.end()); 	// 快速排序
        return A;
    }
};

时间复杂度： $O (n l o g n)$ ，其中 n 是数组 nums 的长度。
空间复杂度： $O (l o g n)$ 。除了存储答案的数组以外，我们需要 O(logn) 的栈空间进行排序。

2、双指针法

由于有负数的存在，因此平方后的数组不一定是有序的，所以可以首尾比较排序，往中间遍历，每次选择平方数更大的加入结果数组，然后移动指针。

时间复杂度： $O (n)$ ，其中 n 是数组 nums 的长度。
空间复杂度： $O (1)$ 。除了存储答案的数组以外，我们只需要维护常量空间。

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int n = nums.size();
        int left = 0, right = n-1;  // 左右指针
        vector<int> ans(n, 0);  
        int idx = n-1;              // 数组索引
        while(left <= right){
            if(abs(nums[left]) > abs(nums[right])){ // // 取大的数加入新数组，并移动相应指针
                ans[idx] = nums[left] * nums[left];
                ++left;
            }else{
                ans[idx] = nums[right] * nums[right];
                --right;
            }
            --idx;                  // 更新索引
        }
        return ans;
    }
};

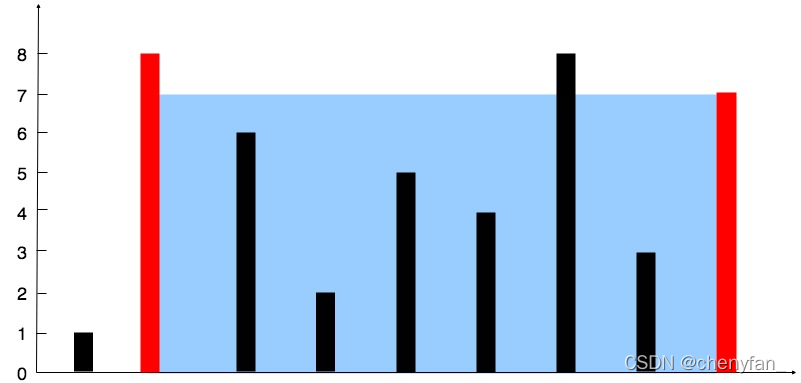
11. 盛最多水的容器 ●●

返回容器可以储存的最大水量。

两个指针初始化位于左右两端，每次循环总是移动高度更小的那一个指针。

因为 面积 = 最小值 min * 长度 L，若不移动更小值指针，则此后的面积都不大于 min * L。
在这里插入图片描述

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int left = 0, right = n-1;
        int maxV = 0;                               // 面积 = 最小值min * 长度L
        while(left < right){                        
            int h = 0;
            if(height[left] > height[right]){       // 总是移动高度更小的那个指针
                h = height[right--];                // 否则得到的面积 不会大于 min * L
            }else{
                h = height[left++];
            }
            maxV = max(maxV, h * (right-left+1));   // 上面指针已经移动，因此要+1
        }
        return maxV;
    }
};

时间复杂度：O(N) ：双指针遍历一次底边宽度 N 。
空间复杂度：O(1)

15. 三数之和 ●●

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。

1、无排序+哈希表，效率低，不更改元素下标

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        unordered_set<int> hash;            // 当前i下的查找哈希
        unordered_set<int> got_hash;        // 当前i下已经存在的答案
        unordered_set<int> got_hash_global; // 存放遍历过的第一个数字
        vector<vector<int>> ans;
        for(int i = 0; i < n-2; ++i){
            if(!got_hash_global.count(nums[i])){    // 当前值是否遍历过
                hash.clear();
                for(int j = i+1; j < n; ++j){
                    int target = -nums[i]-nums[j];  // 寻找的最后一个数
                    if(!got_hash_global.count(target) 
                            && !got_hash.count(target)      // nums[j]不在遍历过的数中，且target不在已经存在的答案或遍历过的数中
                            && !got_hash_global.count(nums[j])){                       
                        if(hash.count(target)){
                            ans.push_back({nums[i],nums[j],target});
                            got_hash.emplace(nums[j]);  
                            got_hash.emplace(target);
                            continue;
                        }                          
                    }
                    hash.emplace(nums[j]);
                }    
                got_hash.clear();           // 清空当前i下已经存在的答案
                got_hash_global.emplace(nums[i]);   // nums[i]已遍历过
            }
        }
        return ans;
    }
};

2、排序+哈希表，更改元素下标，思路更清晰

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> ans;			// 找到答案{a, b, c} a+b+c=0
        unordered_set<int> hash;
        sort(nums.begin(),nums.end());		// 排序
        for(int i = 0; i < n-2; ++i){
            if(nums[i] > 0) break;				// 排序后a大于0时，退出循环
            if(i > 0 && nums[i] == nums[i-1]) continue;	// a值去重复
            hash.clear();						// 清空上一次遍历的哈希表
            for(int j = i+1; j < n; ++j){
                if(j > i + 2 && nums[j] == nums[j-2]) continue;	// b值去重复
                int target = -nums[i] -nums[j];	// 找c值
                if(hash.count(target)){
                    ans.push_back({nums[i], nums[j], target});
                    hash.erase(target);			// c值去重复
                }else{
                	hash.emplace(nums[j]);		// 加入哈希表，可选值
                }
            }
        }
        return ans;
    }
};

3、排序+双指针法（推荐方法）

在这里插入图片描述
首先将数组排序，然后有一层 for 循环，i 从下标0的地方开始，左指针 left = i+1，右指针 right = n-1。

依然还是在数组中找到 abc 使得a + b +c =0，我们这里相当于 a = nums[i]， b = nums[left]， c = nums[right]。

如果 nums[i] + nums[left] + nums[right] > 0 ，right–；
如果 nums[i] + nums[left] + nums[right] < 0 ，left++。

去重操作：对 a（即下标i的元素）去重，以及查找到之后对左右指针的操作，把其中一个指针移动到元素不重复的位置。

时间复杂度： $O(n^2)$ ，数组排序 O(NlogN) + 遍历数组 O(n) * 双指针遍历 O(n)
空间复杂度： $O (1)$

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> ans;
        sort(nums.begin(),nums.end());				// 排序
        for(int i = 0; i < n-2; ++i){
            if (nums[i] > 0) {						// a > 0 退出查找
                return ans;
            }
            if(i > 0 && nums[i] == nums[i-1]){		// a 去重
                continue;
            }
            int l = i+1;							// 定义左右指针
            int r = n-1;
            while(l < r){
                int sum = nums[i] + nums[l] + nums[r];
                if(sum > 0){						// 移动指针
                    --r;
                } else if(sum < 0){
                    ++l;
                } else{								// 找到目标值
                    ans.push_back({nums[i], nums[l], nums[r]});
					// 将左右指针移动到不重复的元素下标上
                    while(l < r && nums[r] == nums[r-1]){
                        --r;
                    }
                    while(l < r && nums[l] == nums[l+1]){
                        ++l;
                    }
                    --r;
                    ++l;
                }
            }            
        }
        return ans;
    }
};

18. 四数之和 ●●

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 $[n u m s [a], n u m s [b], n u m s [c], n u m s [d]]$ （若两个四元组元素一一对应，则认为两个四元组重复）：

–
$0 <= a, b, c, d < n$
a、b、c 和 d 互不相同
$n u m s [a] + n u m s [b] + n u m s [c] + n u m s [d] == t a r g e t$

–
你可以按 任意顺序 返回答案。

排序+双指针

与 15. 三数之和 解法类似，多套一层for循环，但是要注意此时的剪枝操作，不要判断 nums[i] > target 就返回了，因为 target 是任意值。

时间复杂度： $O(n^3)$ ，其中 n 是数组的长度。排序的时间复杂度是 $O (n l o g n)$ ，枚举四元组的时间复杂度是 $O(n^3)$
空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度主要取决于排序额外使用的空间（快排递归调用栈）。此外排序修改了输入数组 nums，实际情况中不一定允许，因此也可以看成使用了一个额外的数组存储了数组 nums 的副本并排序，空间复杂度为 O(n)。

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        int n = nums.size();
        vector<vector<int>> ans;
        sort(nums.begin(), nums.end());                     // 排序
        for(int i = 0; i < n-3; ++i){
            if(nums[i] > target && nums[i] > 0) break;      // 剪枝
            if(i>0 && nums[i] == nums[i-1]) continue;       // a去重
            for(int j = i+1; j < n; ++j){
                // if(nums[j] > target) break;
                if(j>i+1 && nums[j] == nums[j-1]) continue; // b去重
                int l = j+1;
                int r = n-1;
                while(l < r){                               // 移动指针
                    // int sum = nums[i] + nums[j] + nums[l] + nums[r];    // 可能溢出
                    if(nums[i] + nums[j] > target - nums[l] - nums[r]){
                        --r;
                    }else if(nums[i] + nums[j] < target - nums[l] - nums[r]){
                        ++l;
                    }else{
                        ans.push_back(vector<int>{nums[i], nums[j], nums[l], nums[r]});
                        while(l<r && nums[l] == nums[l+1]){
                            ++l;
                        }
                        while(l<r && nums[r] == nums[r-1]){
                            --r;
                        }
                        ++l;
                        --r;
                    }
                }
            }
        }
        return ans;
    }
};