本文所有图片均引用自班纳教授普林斯顿微积分读本
中文内容则是博主自己的一些见解和抄录

第一章 函数图像和直线

1.1.4 垂线检验

函数是一一映射的，如果一个$f(x)$对应两个值，那么就不是函数
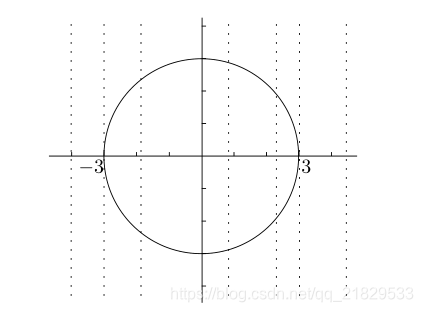
垂线检验便是如此，如果一个图形与同一条垂直于$x$轴的直线有两交点，那么就没有通过垂线检验，不是函数。
如上图，一条与$x$轴垂直的直线$x=1$与曲线$x^2+y^2=9$有两个交点
所以$x^2+y^2=9$不通过垂线检验，即$x^2+y^2=9$不是函数

1.2.1 水平线检验

一个函数存在反函数当且仅当存在每一个$y=f(x)$仅与一个$x$对应。
由此引入水平线检验
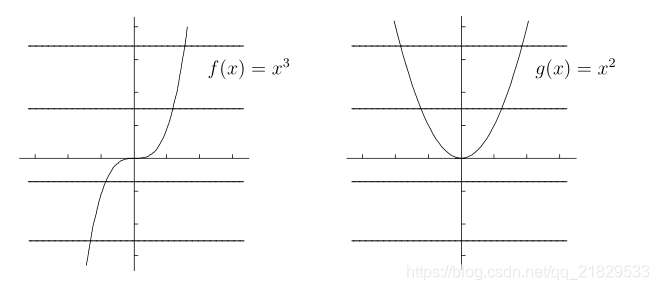
即每条水平线仅与函数图像有一个交点的时候， 该函数才存在反函数
如上图的左图

1.3 复合函数

$f(x)=g(h(x))$ 记为 $f=g○h$
$f(x)=g(x)h(x)$ 记为 $f=gh$
$g(x)=x^2,h(x)=sin(x)$
$g○h=(sin(x){)}^2$
$gh=x^{2}sin(x)$

1.4 奇函数和偶函数

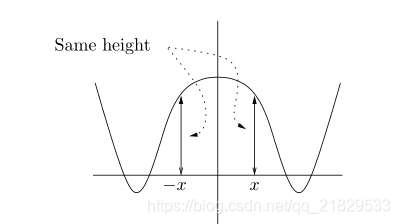
偶函数沿$y$轴对称

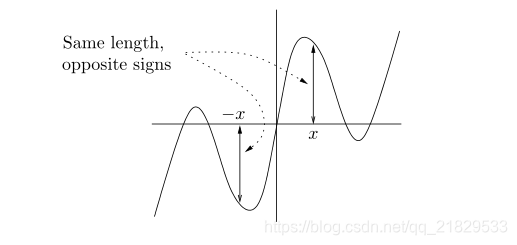
奇函数沿原点中心对称

检验是奇函数还是偶函数的方法：
$f(-x)=-f(x)$ 奇函数
$f(x)=f(-x)$ 偶函数

1.6 常见函数

(1)多项式

f ( x ) = a x n + b