摘要

离散傅里叶变换（DFT）是数字信号处理领域中分析信号频域特性的重要工具，但直接计算DFT的复杂度较高，限制了其在大规模数据处理中的应用。快速傅里叶变换（FFT）的出现显著降低了计算复杂度，极大地推动了数字信号处理技术的发展。本文详细阐述了从DFT到FFT的演变过程，包括DFT的定义、计算复杂度问题，FFT的原理、算法实现以及其在实际应用中的优势，旨在帮助读者深入理解这一重要的技术变革。

一、引言

在数字信号处理的众多任务中，如信号滤波、频谱分析、通信系统中的调制解调等，频域分析是关键环节。离散傅里叶变换（DFT）为我们提供了将离散时间信号从时域转换到频域的方法，使得我们能够观察信号在不同频率上的分布情况。然而，DFT的直接计算涉及大量的乘法和加法运算，计算复杂度较高，尤其是当信号长度较长时，计算时间会显著增加，这在实际应用中成为了一个瓶颈。为了解决这一问题，快速傅里叶变换（FFT）应运而生。FFT通过巧妙的算法设计，大大减少了计算量，提高了计算效率，使得频域分析能够在更短的时间内完成，从而推动了数字信号处理技术在各个领域的广泛应用。

二、离散傅里叶变换（DFT）

2.1 DFT的定义

对于长度为 $N$ 的离散时间序列 $x[n]$，$n=0,1,\cdots ,N-1$，其离散傅里叶变换（DFT）定义为：
$$X[k]=\sum _{n=0}^{N-1}x[n]e^{-j\frac{2\pi }{N}kn},k=0,1,\cdots ,N-1$$
其中，$X[k]$ 是长度为 $N$ 的离散频域序列，$k$ 是离散的频率序号，$e^{-j\frac{2\pi }{N}}$ 通常记为 $W_N$，称为旋转因子。

DFT的逆变换（IDFT）定义为：
$$x[n]=\frac{1}{N}\sum _{k=0}^{N-1}X[k]e^{j\frac{2\pi }{N}kn},n=0,1,\cdots ,N-1$$

2.2 DFT的物理意义

DFT将时域的离散序列 $x[n]$ 分解为 $N$ 个不同频率的复指数序列的线性组合，每个复指数序列的频率为 $${\omega }_k=\frac{2\pi }{N}k$$$k=0,1,\cdots ,N-1$。$X[k]$ 表示序列 $x[n]$ 在频率 ${\omega }_k$ 处的频谱分量，其幅度 $|X[k]|$ 反映了该频率分量的强度，相位 $\angle X[k]$ 反映了该频率分量的相位信息。通过DFT，我们可以在频域中分析信号的频率成分，了解信号的特性。

2.3 DFT的计算复杂度

直接计算DFT时，对于每个 $k$ 值，需要进行 $N$ 次复数乘法和 $N-1$ 次复数加法。由于 $k$ 有 $N$ 个取值，所以总的复数乘法次数约为 $N^2$ 次，复数加法次数约为 $N(N-1)$ 次。当 $N$ 较大时，计算量会急剧增加。例如，当 $N=1024$ 时，直接计算DFT需要进行约 $1024^2=1048576$ 次复数乘法，这对于实时性要求较高的应用来说是难以承受的。因此，DFT计算复杂度高的问题限制了其在实际中的广泛应用。

三、快速傅里叶变换（FFT）的原理

3.1 分治思想的引入

为了降低DFT的计算复杂度，人们提出了快速傅里叶变换（FFT）算法。FFT的核心思想是利用分治策略，将一个 $N$ 点的DFT分解为多个较短长度的DFT来计算。以基 - 2时间抽取FFT算法为例（假设 $N=2^M$，$M$ 为正整数），把 $N$ 点序列 $x[n]$ 按 $n$ 的奇偶性分为两个 $N/2$ 点的子序列：

• 偶数序号子序列：$x_1[r]=x[2r]$，$r=0,1,\cdots ,N/2-1$
• 奇数序号子序列：$x_2[r]=x[2r+1]$，$r=0,1,\cdots ,N/2-1$

则 $N$ 点DFT $X[k]$ 可以表示为：
$$\begin{array}{rl}X[k]& =\sum _{n=0}^{N-1}x[n]W_N^{kn}\\ & =\sum _{r=0}^{N/2-1}x[2r]W_N^{k(2r)}+\sum _{r=0}^{N/2-1}x[2r+1]W_N^{k(2r+1)}\\ & =\sum _{r=0}^{N/2-1}{x}_1[r]W_{N/2}^{kr}+W_N^k\sum _{r=0}^{N/2-1}{x}_2[r]W_{N/2}^{kr}\\ & =X_1[k]+W_N^k{X}_2[k],k=0,1,\cdots ,N-1\end{array}$$
其中 $$W_N=e^{-j\frac{2\pi }{N}}$$ $$W_{N/2}=e^{-j\frac{2\pi }{N/2}}=e^{-j\frac{4\pi }{N}}$$ $X_1[k]$ 和 $X_2[k]$ 分别是 $x_1[r]$ 和 $x_2[r]$ 的 $N/2$ 点DFT。

由于 $X_1[k]$ 和 $X_2[k]$ 具有周期性，即 $$X_1[k+N/2]=X_1[k]$$ $$X_2[k+N/2]=X_2[k]$$ 所以 $X[k]$ 可以进一步表示为：
$$\{\begin{array}{ll}X[k]=X_1[k]+W_N^k{X}_2[k],& k=0,1,\cdots ,N/2-1\\ X[k+N/2]=X_1[k]-W_N^k{X}_2[k],& k=0,1,\cdots ,N/2-1\end{array}$$

这样，一个 $N$ 点的DFT就可以通过两个 $N/2$ 点的DFT来计算。继续对 $N/2$ 点的DFT进行分解，直到分解为2点的DFT，最终可以将计算复杂度从 $O(N^2)$ 降低到 $O(N{\log }_{2}N)$。

3.2 旋转因子的特性

旋转因子 $W_N=e^{-j\frac{2\pi }{N}}$ 具有以下重要特性，这些特性在FFT算法中起到了关键作用：

• 周期性：$W_N^{k+N}=W_N^k$，这是因为 $$e^{-j\frac{2\pi }{N}(k+N)}=e^{-j\frac{2\pi }{N}k}{e}^{-j2\pi }=e^{-j\frac{2\pi }{N}k}$$利用周期性，我们可以避免重复计算旋转因子的值。
• 对称性：$W_N^{k+N/2}=-W_N^k$，因为 $$W_N^{k+N/2}=e^{-j\frac{2\pi }{N}(k+N/2)}=e^{-j\frac{2\pi }{N}k}{e}^{-j\pi }=-e^{-j\frac{2\pi }{N}k}=-W_N^k$$对称性可以减少旋转因子的计算量，进一步提高算法效率。

3.3 蝶形运算

蝶形运算是FFT算法中的基本运算单元。对于基 - 2 FFT算法，一个蝶形运算涉及两个输入数据 $a$ 和 $b$，以及一个旋转因子 $W_N^k$，其输出为：
$$\{\begin{array}{l}A=a+W_N^{k}b\\ B=a-W_N^{k}b\end{array}$$

在基 - 2时间抽取FFT算法中，每一级都由多个蝶形运算组成。通过不断地进行蝶形运算，最终可以得到 $N$ 点的FFT结果。蝶形运算的优点是只需要一次复数乘法和两次复数加法，大大减少了计算量。

四、FFT算法的实现

4.1 基 - 2 时间抽取 FFT 算法的实现步骤

4.1.1 输入序列的重排

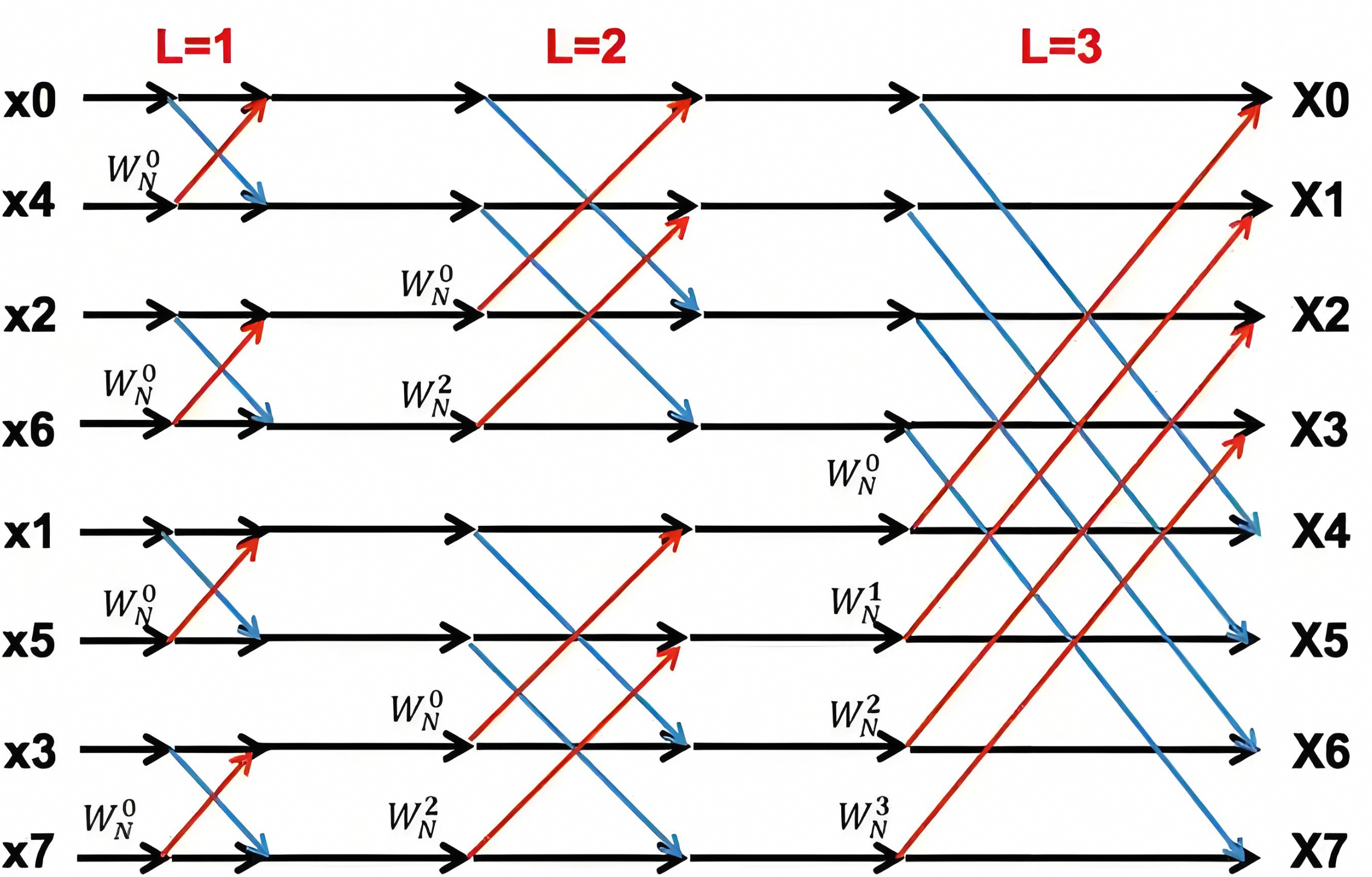
在基 - 2 时间抽取 FFT 算法中，输入序列 $x[n]$ 需要按照比特倒序的方式进行重排。假设序列长度 $N=2^M$，对于序号 $n$，将其表示为 $M$ 位二进制数，然后将这 $M$ 位二进制数按位反转得到新的序号 $n^{\prime }$，将 $x[n]$ 放置到 $x[n^{\prime }]$ 的位置。例如，当 $N=8$（$M=3$）时，$n=3$ 的二进制表示为 $011$，比特倒序后为 $110$，即 $6$，那么 $x[3]$ 要与 $x[6]$ 交换位置。这样做的目的是为后续的蝶形运算提供方便，使得运算可以按照规则的顺序进行。

4.1.2 多级蝶形运算

将重排后的序列进行 $M$ 级蝶形运算，每一级包含 $N/2$ 个蝶形单元。以第 $m$ 级（$m=1,2,\cdots ,M$）为例，同一级中每个蝶形单元的旋转因子为 $$W_N^{r{2}^{M-m}}$$其中 $r=0,1,\cdots ,2^{m-1}-1$。每一级的蝶形运算都根据前面提到的蝶形运算公式 $$A=a+W_N^{k}b$$ 和 $$B=a-W_N^{k}b$$ 进行计算，不断更新序列的值。

下面是一个用 Python 实现基 - 2 时间抽取 FFT 算法的示例代码：

import numpy as np

def bit_reverse(x):
    N = len(x)
    M = int(np.log2(N))
    x_reversed = np.zeros(N, dtype=complex)
    for n in range(N):
        binary_n = bin(n)[2:].zfill(M)
        reversed_n = int(binary_n[::-1], 2)
        x_reversed[n] = x[reversed_n]
    return x_reversed

def fft(x):
    N = len(x)
    if N <= 1:
        return x
    x = bit_reverse(x)
    M = int(np.log2(N))
    for m in range(1, M + 1):
        group_size = 2**m
        half_group_size = group_size // 2
        for k in range(0, N, group_size):
            for r in range(half_group_size):
                W = np.exp(-2j * np.pi * r / group_size)
                a = x[k + r]
                b = x[k + r + half_group_size]
                x[k + r] = a + W * b
                x[k + r + half_group_size] = a - W * b
    return x

4.2 其他 FFT 算法变体

除了基 - 2 时间抽取 FFT 算法，还有基 - 2 频率抽取 FFT 算法、基 - 4 FFT 算法以及分裂基 FFT 算法等。

4.2.1 基 - 2 频率抽取 FFT 算法

基 - 2 频率抽取 FFT 算法与基 - 2 时间抽取 FFT 算法类似，但它是在频域进行分解。它将 $N$ 点 DFT 分解为两个 $N/2$ 点 DFT 的组合，不过分解的方式和蝶形运算的结构与时间抽取算法有所不同。频率抽取算法在输入序列不需要进行比特倒序重排，而是在输出序列进行比特倒序，这在某些应用场景中可能更具优势。

4.2.2 基 - 4 FFT 算法

当序列长度 $N$ 是 4 的幂次方（即 $N=4^M$）时，可以使用基 - 4 FFT 算法。基 - 4 算法将 $N$ 点 DFT 分解为四个 $N/4$ 点 DFT，相比于基 - 2 算法，它能进一步减少乘法运算的次数。因为基 - 4 蝶形运算可以用更少的乘法实现，从而提高计算效率。

4.2.3 分裂基 FFT 算法

分裂基 FFT 算法结合了基 - 2 和基 - 4 算法的优点，它在分解过程中根据序列长度灵活地采用基 - 2 和基 - 4 的分解方式。分裂基算法在计算效率上通常优于单纯的基 - 2 或基 - 4 算法，尤其是对于较长的序列，能显著减少乘法和加法的运算次数。

五、FFT 相对于 DFT 的优势

5.1 计算复杂度的显著降低

如前文所述，直接计算 DFT 的复杂度为 $O(N^2)$，而 FFT 算法（如基 - 2 时间抽取 FFT）的复杂度为 $O(N{\log }_{2}N)$。当 $N$ 较大时，$N{\log }_{2}N$ 远小于 $N^2$。例如，当 $N=1024$ 时，DFT 需要约 $1024^2=1048576$ 次复数乘法，而基 - 2 FFT 只需要约 $\frac{1024}{2}{\log }_{2}1024=512\times 10=5120$ 次复数乘法，计算效率得到了极大的提高。这使得 FFT 能够处理更长的信号序列，并且在更短的时间内完成频域分析任务。

5.2 实时处理能力的提升

在许多实际应用中，如音频和视频处理、雷达信号处理等，对信号处理的实时性要求很高。由于 FFT 算法大大减少了计算量，使得系统能够在更短的时间内完成频域分析，从而满足实时处理的需求。例如，在音频实时特效处理中，通过 FFT 可以快速分析音频信号的频谱，然后根据频谱信息进行滤波、均衡等处理，最后通过逆 FFT 将处理后的频谱转换回时域，实现实时的音频效果调整。

5.3 硬件实现的可行性增强

较低的计算复杂度使得 FFT 更容易在硬件上实现。相比于 DFT 所需的大量乘法器和加法器，FFT 算法的规则结构和较少的运算次数使得它可以用更简单的硬件电路来实现。例如，在现场可编程门阵列（FPGA）和专用集成电路（ASIC）中，FFT 模块可以高效地实现，从而为各种嵌入式系统和实时信号处理设备提供强大的频域处理能力。

六、FFT 在实际应用中的广泛应用

6.1 音频处理

在音频处理领域，FFT 被广泛应用于音频的频谱分析、滤波、压缩等方面。通过 FFT 可以将音频信号从时域转换到频域，分析音频信号的频率成分，例如检测音频中的高音、低音成分，以及识别音频中的特定频率特征，如人声的基频和各次谐波。在音频滤波中，可以根据频谱分析的结果设计滤波器，去除不需要的频率成分，如噪声。在音频压缩方面，FFT 可以帮助确定音频信号的主要频率分量，然后对这些分量进行量化和编码，从而实现音频数据的压缩。

6.2 图像处理

在图像处理中，FFT 用于图像的频域滤波、特征提取等操作。图像的低频成分对应着图像的整体轮廓和缓慢变化的部分，高频成分对应着图像的细节和边缘信息。通过对图像进行二维 FFT 变换，可以将图像从空间域转换到频域，然后在频域中对图像进行滤波处理。例如，使用低通滤波器可以平滑图像，去除图像中的高频噪声；使用高通滤波器可以增强图像的边缘信息，使图像更加清晰。此外，FFT 还可以用于图像的特征提取，通过分析图像的频谱特征来识别图像中的物体或模式。

6.3 通信系统

在通信系统中，FFT 是正交频分复用（OFDM）技术的核心算法。OFDM 是一种高效的多载波调制技术，它将高速数据流分成多个低速子数据流，每个子数据流在不同的子载波上进行传输。FFT 和逆 FFT 用于实现 OFDM 信号在频域和时域之间的转换。在发射端，通过逆 FFT 将频域的子载波数据转换为时域的 OFDM 符号；在接收端，通过 FFT 将接收到的时域 OFDM 符号转换回频域，然后进行解调。FFT 的高效计算使得 OFDM 技术能够在有限的频谱资源下实现高速、可靠的通信。

6.4 雷达信号处理

在雷达信号处理中，FFT 用于对雷达回波信号进行频谱分析，以确定目标的速度、距离等信息。雷达发射的信号遇到目标后会产生回波，回波信号包含了目标的各种信息。通过对回波信号进行 FFT 变换，可以得到其频谱特性，根据多普勒频移原理计算目标的速度；根据回波信号的延迟时间和频率信息，可以估计目标的距离。FFT 的快速计算能力使得雷达系统能够实时地对目标进行检测和跟踪。

七、结论

从离散傅里叶变换（DFT）到快速傅里叶变换（FFT）的发展是数字信号处理领域的一个重要里程碑。DFT 为我们提供了一种将离散时间信号从时域转换到频域的基本方法，但由于其计算复杂度高，限制了其在大规模数据处理和实时应用中的使用。FFT 算法通过引入分治思想，利用旋转因子的特性和蝶形运算，成功地将计算复杂度从 $O(N^2)$ 降低到 $O(N{\log }_{2}N)$，大大提高了计算效率。

FFT 不仅在计算复杂度上具有显著优势，还提升了信号处理的实时性和硬件实现的可行性。它在音频处理、图像处理、通信系统、雷达信号处理等众多实际应用领域发挥着至关重要的作用，推动了这些领域的技术发展。随着科技的不断进步，FFT 算法也在不断改进和优化，出现了多种变体算法，以适应不同的应用场景和需求。