首先我们看看归并排序
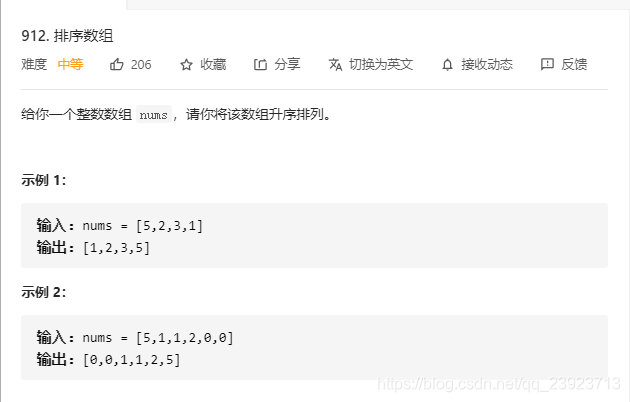
题目:
思路:
自底向上
1.MergeSort函数一直二分到只有一个元素,
2.Merge函数代表合并已经两个已经排序的数组(双指针法)
3.回溯过程在MergeSort函数中,回溯也就是自底向上的过程
代码:
class Solution {
private:
void Merge(vector<int> &arr, int start, int end,int mid, vector<int> &temparr)
{
int i_start = start;
int i_end = mid;
int j_start = mid + 1;
int j_end = end;
int length = 0;
//合并两个有序序列(为什么就有序了) 思考!!!
while (i_start<= i_end&& j_start<= j_end)//两个有序数组合并后可能会有个对于的
{
if (arr[i_start]< arr[j_start])
{
temparr[length] = arr[i_start];
length++;
i_start++;
}
else
{
temparr[length] = arr[j_start];
length++;
j_start++;
}
}
while (i_start<= i_end)//这是判断的
{
temparr[length] = arr[i_start];
length++;
i_start++;
}
while (j_start <= j_end)
{
temparr[length] = arr[j_start];
length++;
j_start++;
}
//辅助空间数据覆盖到原空间
for (int i=0;i<length;i++)
{
arr[start+i]=temparr[i];
}
}
void MergeSort(vector<int> &arr, int start, int end, vector<int> &temparr)
{
if (start>=end)
{
return;
}
//划分到最后是每一个里面只有一个数据
int mid = (start + end) / 2;
MergeSort(arr,start,mid, temparr);
MergeSort(arr, mid+1, end, temparr);
Merge(arr, start, end, mid, temparr);
}
public:
vector<int> sortArray(vector<int>& nums)
{
int left=0;
int right=nums.size()-1;
vector<int> temparr(nums.size(),0);
MergeSort(nums, left, right,temparr);
return nums;
}
};
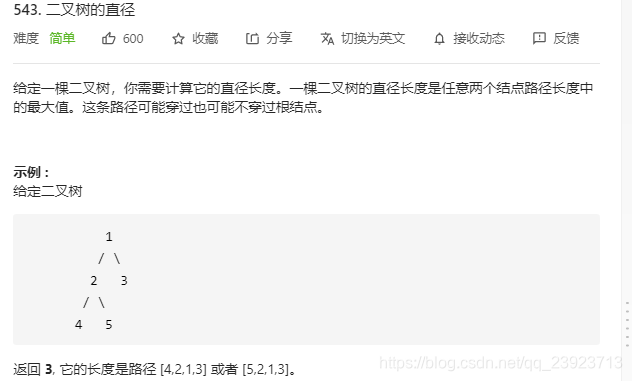
题目
思路
这题运用到了归并的思想,代码中
代码:
dfs函数采用自底向上的写法
自底向上特征
maxlen代表最大直径中的结点数 因此最终主函数返回值 是maxlen-1
int dfs(TreeNode* root)
{
if(root==NULL) return 0;
int leftMax=dfs(root->left);
int rightMax=dfs(root->right);
......//函数功能
.....
return ..}
函数功能**(返回值)** 代表着当前节点(包含当前节点)以下的最大深度
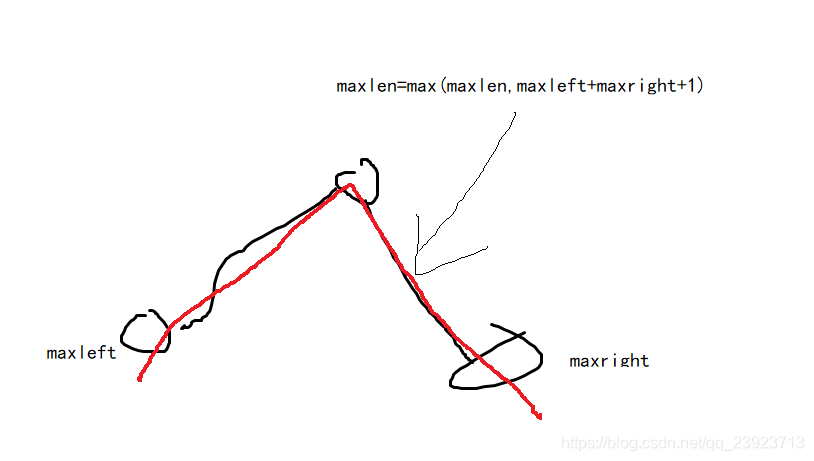
显然我们应该更新maxlen的时候是(下面的灵魂手绘)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
int maxLen=0;
int dfs(TreeNode* root)
{
if(root==NULL) return 0;
int leftMax=dfs(root->left);
int rightMax=dfs(root->right);
maxLen=max(maxLen,leftMax+rightMax+1);
return max(leftMax,rightMax)+1;//这个是与上层链接的这层节点一下(包含本节点)的最大深度
}
public:
int diameterOfBinaryTree(TreeNode* root) {
if(root==NULL) return 0;
dfs(root);
return maxLen-1;
}
};
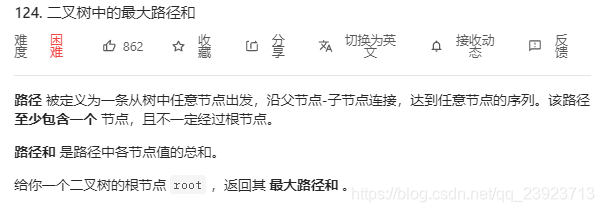
题目:
思路:
首先dfs函数
1.采用至下而上的方法,也就是一直递归至最终的叶子节点的下一个节点,然后回溯,
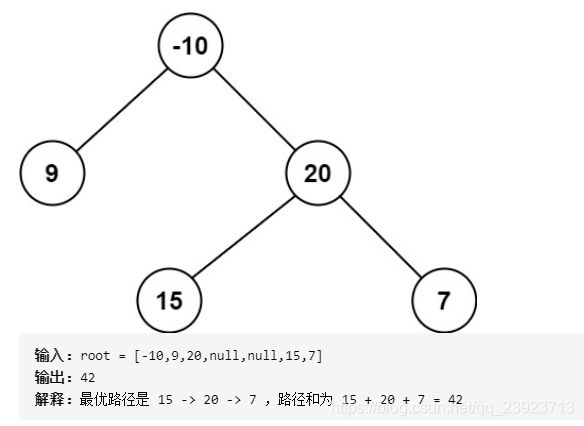
2.主要功能是 求当前节点(包含当前节点)以及下面节点的最长的一个和(可能是负数) ,也就是说是一天直线,(没有转弯)。
3.我们更新ret_max的情况就是
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int ret_max=INT_MIN;
int dfs(TreeNode* root)//dfs求当前节点以及下面节点的最长的一个和(可能是负数) ,也就是说是一天直线,(没有转弯)
{
if(root==nullptr) return 0;
int leftMax=max(dfs(root->left),0);//保证是正数,负数的时候,代表下面的节点我们可以舍弃
int righrMax=max(dfs(root->right),0);//同理
ret_max=max(ret_max,leftMax+righrMax+root->val);
return max(leftMax,righrMax)+root->val;
}
public:
int maxPathSum(TreeNode* root)
{
//if(root==nullptr) return 0; //题目中强调了二叉树至少有一个节点
dfs(root);
return ret_max;
}
};
题目:
思路:
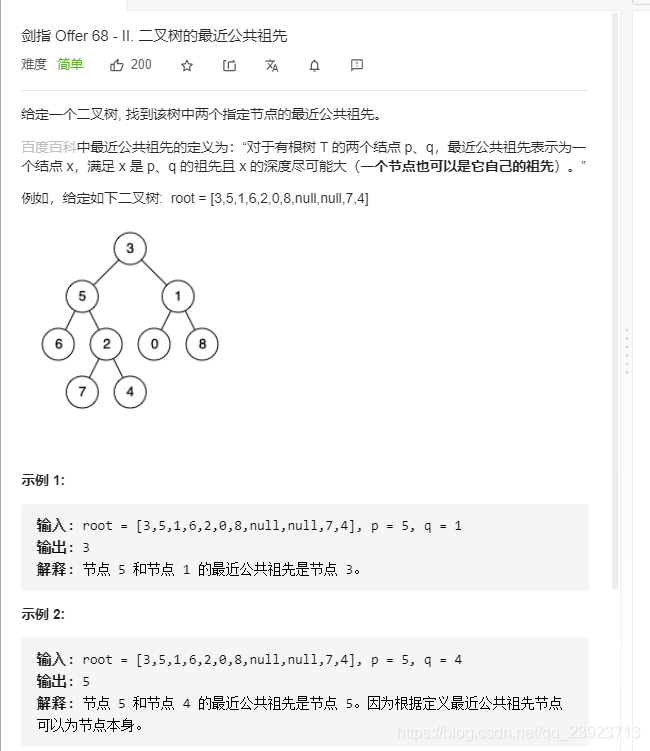
由于是搜索数,阴齿自上而下可以解决。
代码:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
if(root==NULL) return NULL;
if(root->val>p->val&&root->val>q->val)
{
return lowestCommonAncestor(root->left,p,q);
}
if(root->val<p->val&&root->val<q->val)
{
return lowestCommonAncestor(root->right,p,q);
}
return root;
}
};
题目
思路:
递归+回溯
自下而上(有局部终止)
1.lowestCommonAncestor找到叶子节点的下一个节点或则p,q节点就返回
2.主要功能是寻找当前节点以及以下节点的是p,q的最近公共祖先
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
if(root==NULL||root==p||root==q) return root;
TreeNode* leftNode=lowestCommonAncestor(root->left,p,q);
TreeNode* rightNode=lowestCommonAncestor(root->right,p,q);
if(leftNode==NULL&&rightNode==NULL) return NULL;
else if(leftNode==NULL&&rightNode!=NULL) return rightNode;
else if(leftNode!=NULL&&rightNode==NULL) return leftNode;
else return root;
}
};