最近想将剑指 Offer 13 重新刷一遍，因为之间是在leetcode上面做的题目，现在在牛客上面，我发现有些边界条件牛客没给出，但是面试基本手撕代码都是在牛客上面。

题目：
牛客：剑指 Offer 13. 机器人的运动范围

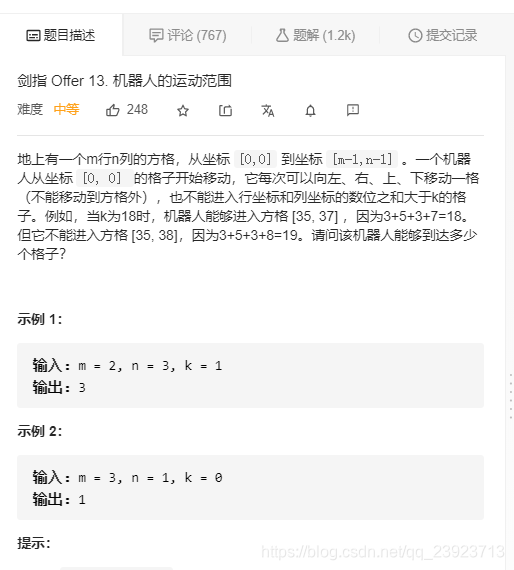
leetcode：剑指 Offer 13. 机器人的运动范围

思路：

首先我们做这种题目是需要有一些必须写出的函数。边界函数isArea() 还有个记录是否访问的二维数组used以及方向增量数组dxy

   bool isArea(int rows, int cols,int temp_i,int temp_j)
    {
        if(temp_i<0||temp_i>=rows||temp_j<0||temp_j>=cols) return false;
        
        
        return true;
    }

记录是否访问过的二维数组used

vector<vector<bool>> used(rows,vector<bool>(cols,false));

方向增量数组

    vector<vector<int>> dxy{{0,1},{1,0},{0,-1},{-1,0}};

现在开始分析题意，题目要求是可到达的位置数目，也就是说明重复走过的格子不用再走了，显然是flood fill的意思（used每次访问设置true，在往回走时不用恢复为false）

这题题目说不能进入行坐标和列坐标的数位之和大于k的格子
需要一个函数getLegal

  int getLegal(int temp_i,int temp_j,int threshold)
    {
        int sum=0;
        
        while(temp_i!=0)
        {
            sum=sum+temp_i%10;
            
            temp_i=temp_i/10;
        }
        
         while(temp_j!=0)
        {
            sum=sum+temp_j%10;
            
            temp_j=temp_j/10;
        }
        
        return threshold>=sum;
    }

方法一：
万能的dfs ，我们在dfs中注意used设置为true就不用再恢复了

方法二：广度优先遍历bfs

我们需要注意队列中存的是pair<int,int> node,相关的值是node.first,node.second.

class Solution {

private: 
    vector<vector<int>> dxy{{0,1},{1,0},{0,-1},{-1,0}};
    

    bool isArea(int rows, int cols,int temp_i,int temp_j)
    {
        if(temp_i<0||temp_i>=rows||temp_j<0||temp_j>=cols) return false;
        
        
        return true;
    }
    
    int getLegal(int temp_i,int temp_j,int threshold)
    {
        int sum=0;
        
        while(temp_i!=0)
        {
            sum=sum+temp_i%10;
            
            temp_i=temp_i/10;
        }
        
         while(temp_j!=0)
        {
            sum=sum+temp_j%10;
            
            temp_j=temp_j/10;
        }
        
        return threshold>=sum;
    }
    void dfs(int rows, int cols,int current_i,int current_j,  vector<vector<bool>>&used,int threshold )
    {
        
        for(int i=0;i<dxy.size();i++)
        {
            int temp_i=current_i+dxy[i][0];
            int temp_j=current_j+dxy[i][1];
            
            if(isArea( rows,  cols,  temp_i,  temp_j)&&used[temp_i][temp_j]==false&&getLegal( temp_i,  temp_j,  threshold))
            {
                used[temp_i][temp_j]=true;
          
                dfs( rows,  cols,  temp_i,  temp_j, used,  threshold);
                
            }
        }
    }
    
public:
    int movingCount(int threshold, int rows, int cols) 
    {
        int start_i=0;
        int start_j=0;
        
        vector<vector<bool>> used(rows,vector<bool>(cols,false));
        
        if(isArea( rows,  cols,  start_i, start_j)==false||used[start_i][start_j]==true||getLegal( start_i,  start_j,  threshold)==false)  return 0;
 
        used[start_i][start_j]=true;
        
        dfs(   rows,  cols, start_i, start_j,used,threshold);
        int count=0;
        
        for(int i=0;i<rows;i++)
        {
               for(int j=0;j<cols;j++)
               {
                   if(used[i][j]==true) count++;
               }
        }
        return count;
        
    }
};

方法二： 使用队列进行广度优先遍历

class Solution {

private: 
    vector<vector<int>> dxy{{0,1},{1,0},{0,-1},{-1,0}};
    

    bool isArea(int rows, int cols,int temp_i,int temp_j)
    {
        if(temp_i<0||temp_i>=rows||temp_j<0||temp_j>=cols) return false;
        
        
        return true;
    }
    
    int getLegal(int temp_i,int temp_j,int threshold)
    {
        int sum=0;
        
        while(temp_i!=0)
        {
            sum=sum+temp_i%10;
            
            temp_i=temp_i/10;
        }
        
         while(temp_j!=0)
        {
            sum=sum+temp_j%10;
            
            temp_j=temp_j/10;
        }
        
        return threshold>=sum;
    }
    void dfs(int rows, int cols,int current_i,int current_j,  vector<vector<bool>>&used,int threshold )
    {
        
        for(int i=0;i<dxy.size();i++)
        {
            int temp_i=current_i+dxy[i][0];
            int temp_j=current_j+dxy[i][1];
            
            if(isArea( rows,  cols,  temp_i,  temp_j)&&used[temp_i][temp_j]==false&&getLegal( temp_i,  temp_j,  threshold))
            {
                used[temp_i][temp_j]=true;
          
                dfs( rows,  cols,  temp_i,  temp_j, used,  threshold);
                
            }
        }
    }
    
public:
    int movingCount(int threshold, int rows, int cols) 
    {
        int start_i=0;
        int start_j=0;
        
        vector<vector<bool>> used(rows,vector<bool>(cols,false));
        
        if(isArea( rows,  cols,  start_i, start_j)==false||used[start_i][start_j]==true||getLegal( start_i,  start_j,  threshold)==false)  return 0;
 
        used[start_i][start_j]=true;
        
        queue<pair<int,int>> qu;
        
        qu.push({start_i,start_j});
        int count=0;
       while(!qu.empty())
       {
           int n=qu.size();
           count=count+n;
           for(int i=0;i<n;i++)
           {
               auto node=qu.front();
               qu.pop();
               for(int m=0;m<dxy.size();m++)
               {
                   int temp_i=node.first+dxy[m][0];;
                   int temp_j=node.second+dxy[m][1];
                   if(isArea( rows,  cols,  temp_i,  temp_j)&&used[temp_i][temp_j]==false&&getLegal( temp_i,  temp_j,  threshold))
                   {
                       qu.push({temp_i,temp_j});

                       used[temp_i][temp_j]=true;
                   }
                   
               }
               
               
           }
       }
       
        
        return count;
        
    }
};