对一个数组按照给定的下标进行排序，仅仅使用两两交换的方式，要求不能对数组进行扩容，尽可能少的额外空间。

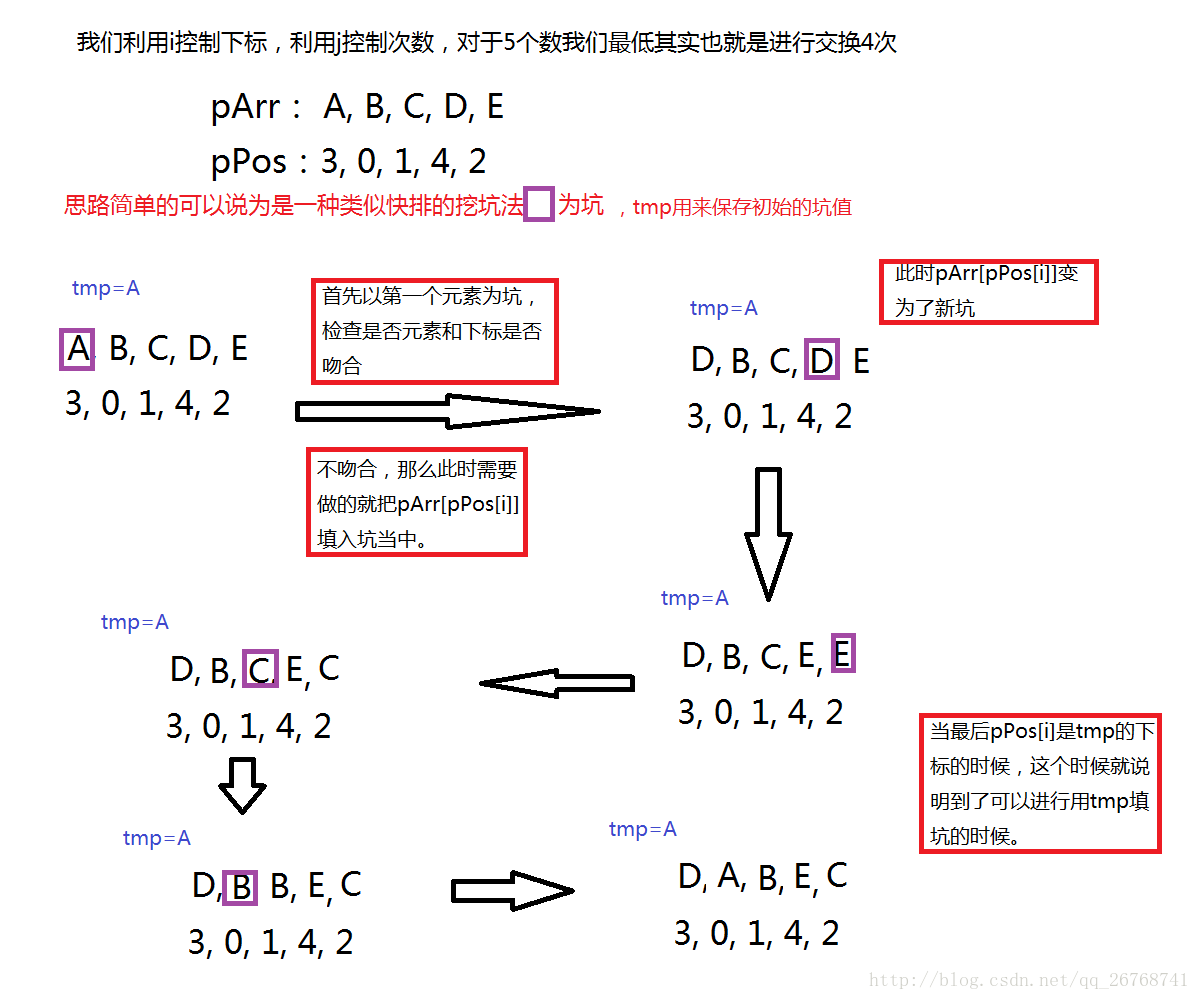
如：原数组为A,B,C,D,E，现在给定的新位置为3，0，1，4，2，那么排序后为D,A,B,E,C,

void SwapSort(int *pArr,int *pPos,int n)

1.解决问题

这是最近看到的一道面试题，感觉突然一下不容易想到，所以特此来写一下：

实现代码：

void SwapSort(int *pArr, int *pPos, int n)
{
    assert(pArr);
    assert(pPos);
    int tmp = pArr[0];
    int i = 0;
    for (int j = 0; j < n; )
    {
        if (pPos[i] != i)
        {
            tmp = pArr[i];
            int prevpos = i;
            while (1)
            {
                pArr[i] = pArr[pPos[i]];
                i = pPos[i];
                j++;
                if (prevpos == pPos[i])
                {
                    pArr[i] = tmp;
                    j++;
                    break;
                }
            }       
        }
        else
        {
            i++;
            j++;
        }
    }
}

2.发散考虑

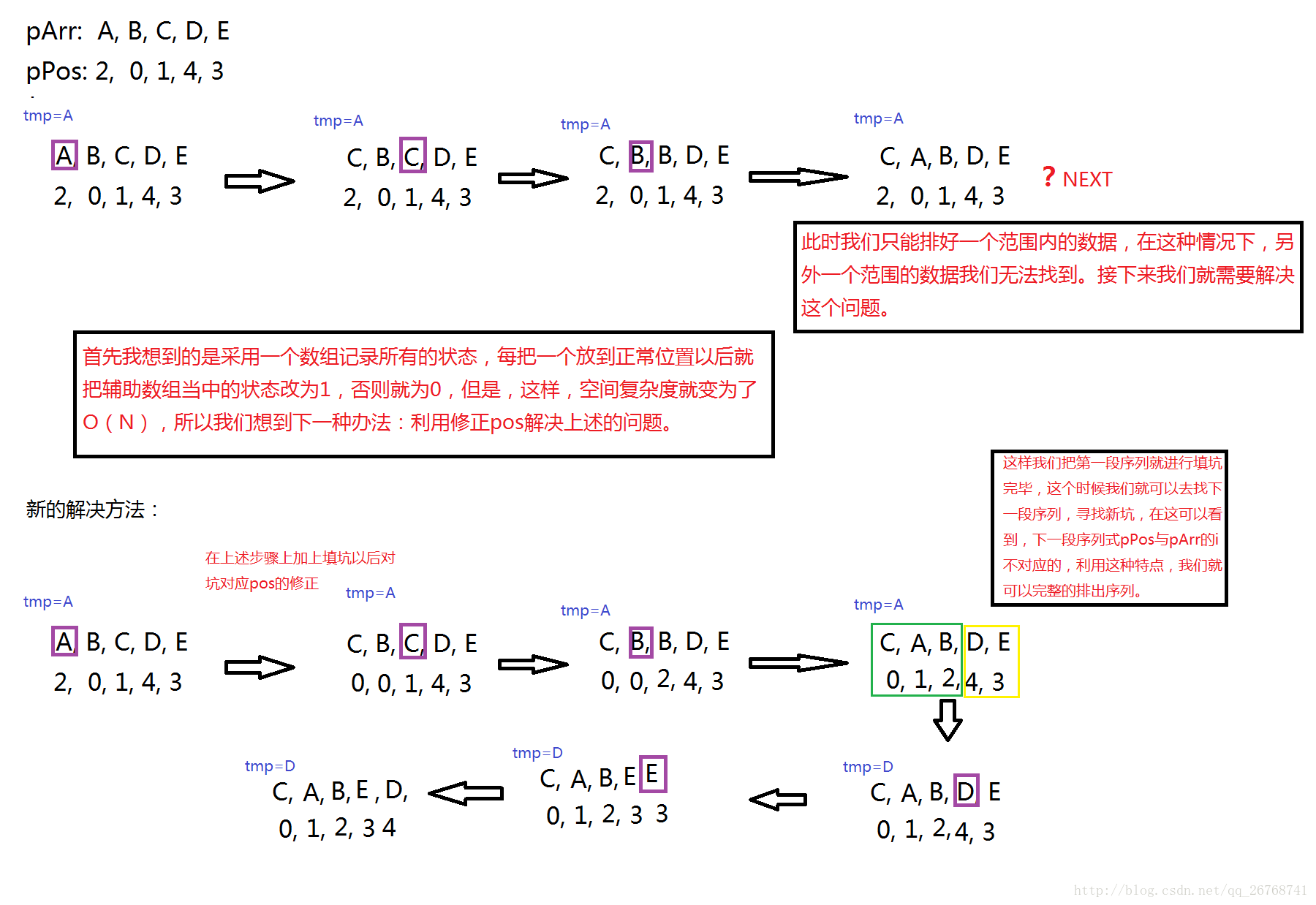
当我写完这种方式的时候，我进行了其他案例的测试

比如我给出了pPos[]={2,0,1,3,4}，或者是pPos[]={3,4,1,0,2}。
最后在这里我总结出一个特点，就是这个时候如果我们按照上述那样操作的话，最终会出现一种问题，只能调整一个范围内的数据成正常顺序，另外一个不相关的范围的顺序就会出问题了。

首先我想到的是采用一个数组记录所有的状态，每把一个放到正常位置以后就把辅助数组当中的状态改为1，否则就为0，但是，这样，空间复杂度就变为了O（N），所以我们想到下一种办法

void swapsort(int *parr, int *ppos, int n)
{
    assert(parr);
    assert(ppos);
    int tmp = parr[0];
    int i = 0;
    for (int j = 0; j < n;)
    {

        while (i == ppos[i])
        {
            i++;
            j++;
        }
        //当全部填充后，可以考虑跳出
        if (i >= n)
            break;
        if (ppos[i] != i)
        {
            tmp = parr[i];
            int prevpos = i;
            while (1)
            {
                parr[i] = parr[ppos[i]];
                int newpos = ppos[i];
                ppos[i] = i;
                i = newpos;
                j++;
                if (prevpos == ppos[i])
                {
                    parr[i] = tmp;
                    ppos[i] = i;
                    i = prevpos + 1;
                    j++;
                    break;
                }
            }
        }   
    }
}

3.总结

对于面试题中好多东西我们是都可能没见过的，但是在这个其中，大部分都是我们见过的一些的变形，所以需要熟练的使用我们所学习的数据结构和算法，当然，前提是对这些结构和算法的概念一定要清楚的记得。