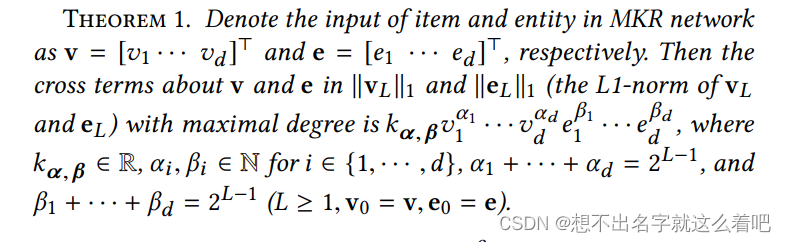Multi-Task Feature Learning for Knowledge Graph Enhanced
1.框架
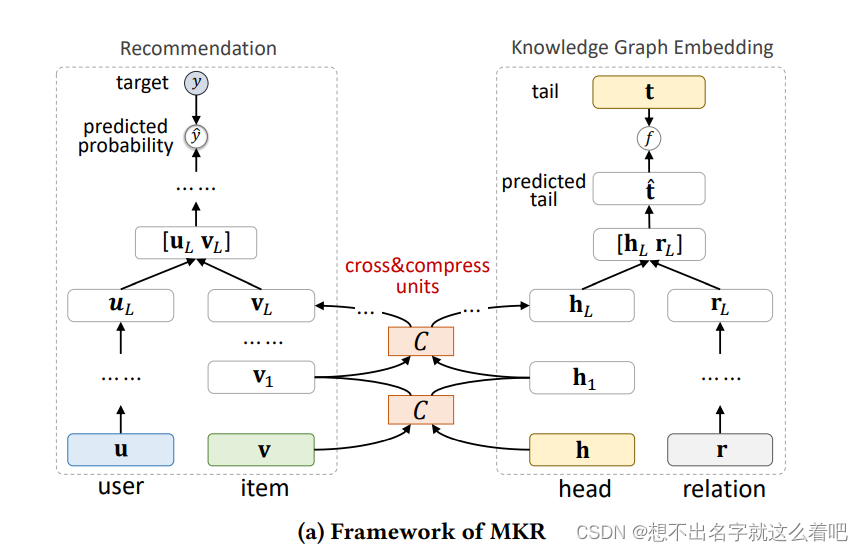
MKR是一个通用的、端对端深度推荐框架,
由三个主要部分组成:推荐模块、KGE模块、交叉压缩单元
旨在利用知识图谱嵌入(KGE)去协助推荐任务。两个任务不相互独立,由于RS中的item和KG中的entity相互联系而高度相关。该框架通过交替优化两个任务来进行训练,使MKR在真实推荐场景中具有高度灵活和适应的特性。
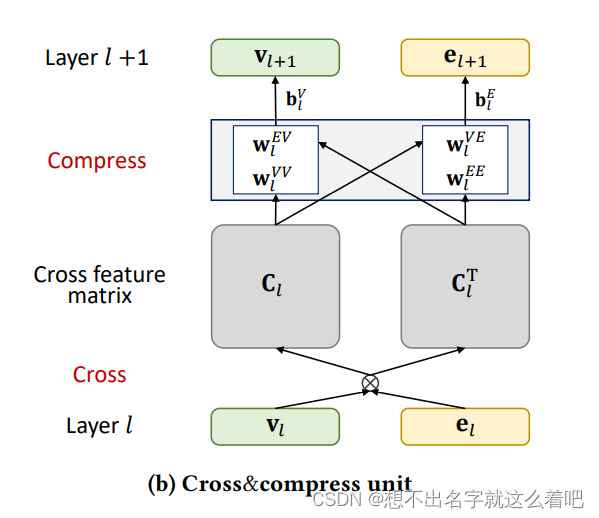
1.1.交叉压缩单元
交叉压缩单元桥接起RS和KG,可以自动学习RS中item和KG中entity的高阶交互特征
cross operation
构造
υ
l
∈
R
d
,
e
l
∈
R
d
的
d
∗
d
p
a
i
r
w
i
s
e
i
n
t
e
r
a
c
t
i
o
n
构造\upsilon_l\in R^d,e_l\in R^d 的d*d\;pairwise\;interaction
构造υl∈Rd,el∈Rd的d∗dpairwiseinteraction
C l = v l e l T = [ υ l ( 1 ) e l ( 1 ) . . . υ l ( 1 ) e l ( d ) υ l ( d ) e l ( 1 ) . . . υ l ( d ) e l ( d ) ] (1) C_l=v_le_l^T=\left[ \begin{matrix} \upsilon_l^{(1)}e_l^{(1)} & ... & \upsilon_l^{(1)}e_l^{(d)} \\ \upsilon_l^{(d)}e_l^{(1)} & ... & \upsilon_l^{(d)}e_l^{(d)} \end{matrix} \right] \tag{1} Cl=vlelT=[υl(1)el(1)υl(d)el(1)......υl(1)el(d)υl(d)el(d)](1)
compress operation
w
l
∈
R
d
和
b
l
∈
R
d
是训练权重和偏差向量,权重向量将交叉特征矩阵从
R
d
∗
d
压缩为
R
d
w_l\in R^d\;和\;b_l\in R^d\;是训练权重和偏差向量,权重向量将交叉特征矩阵从R^{d*d}压缩为R^d
wl∈Rd和bl∈Rd是训练权重和偏差向量,权重向量将交叉特征矩阵从Rd∗d压缩为Rd
υ
l
+
1
=
C
l
w
l
V
V
+
C
l
T
w
l
E
V
+
b
l
V
=
υ
l
e
l
T
w
l
V
V
+
e
l
υ
l
T
w
l
E
V
+
b
l
V
e
l
+
1
=
C
l
w
l
V
E
+
C
l
T
w
l
E
E
+
b
l
E
=
υ
l
e
l
T
w
l
V
E
+
e
l
υ
l
T
w
l
E
E
+
b
l
E
(2)
\upsilon_{l+1}=C_lw_l^{VV}+C_l^Tw_l^{EV}+b_l^V=\upsilon_le_l^Tw_l^{VV}+e_l\upsilon_l^Tw_l^{EV}+b_l^V \\ e_{l+1}=C_lw_l^{VE}+C_l^Tw_l^{EE}+b_l^E=\upsilon_le_l^Tw_l^{VE}+e_l\upsilon_l^Tw_l^{EE}+b_l^E \tag{2}
υl+1=ClwlVV+ClTwlEV+blV=υlelTwlVV+elυlTwlEV+blVel+1=ClwlVE+ClTwlEE+blE=υlelTwlVE+elυlTwlEE+blE(2)
简写为:
[
υ
l
+
1
,
e
l
+
1
]
=
C
(
v
l
,
e
l
)
(3)
[\upsilon_{l+1},e_{l+1}]=C(v_l,e_l) \tag{3}
[υl+1,el+1]=C(vl,el)(3)
1.2.推荐系统
向量u和v分别表示用户和项目,二者可以基于应用场景用one-hot ID,attributes,bag-of-words,或者结合来刻画
给定用户u的原始特征向量u,使用L层的多层感知器MLP提取用户的潜在浓缩的特征:
u
L
=
M
(
M
(
.
.
.
M
(
u
)
)
)
=
M
L
(
u
)
(4)
u_L=M(M(...M(u)))=M^L(u) \tag{4}
uL=M(M(...M(u)))=ML(u)(4)
M是全连接神经网络层:
M
(
x
)
=
σ
(
W
x
+
b
)
(5)
M(x)=\sigma(Wx+b) \tag{5}
M(x)=σ(Wx+b)(5)
对于项目v,通过使用L个交叉压缩单元提取他的特征(S(v)是与项目v相关的实体):
v
L
=
E
e
∼
S
(
v
)
[
C
L
(
v
,
e
)
[
v
]
]
(6)
v_L=E_e\sim S(v)[C^L(v,e)[v]] \tag{6}
vL=Ee∼S(v)[CL(v,e)[v]](6)
推荐系统是点击率预估模块,在得到user特征向量和item特征向量后,通过向量内积或MLP可计算用户u参与项v的可能性:
y
^
u
v
=
σ
(
f
R
S
(
u
L
,
v
L
)
)
(7)
\hat{y}_{uv}=\sigma(f_{RS}(u_L,v_L)) \tag{7}
y^uv=σ(fRS(uL,vL))(7)
1.3.知识图谱嵌入模块
KGE是将entity和relation映射到连续的低维向量空间的同时保留他们原来的空间结构
KGE模型:distance-based translational method、semantic-based matching method
作者提出的模型:deep semantic matching architecture
对于知识三元组(h,r,t),利用交叉压缩单元和多层感知器从原始h和r提取特征,将head和relation对应的向量进行拼接,经过多层网络得到一个tail对应向量的预测值t^(S(h)是和实体h的关联项合集)
h
L
=
E
v
∼
S
(
h
)
[
C
L
(
v
,
h
)
[
e
]
]
r
L
=
M
L
(
r
)
,
t
^
=
M
k
(
[
h
L
r
L
]
)
(8)
h_L=E_v\sim S(h)[C^L(v,h)[e]] \\ r_L=M^L(r), \\ \hat{t}=M^k(\left[ \begin{matrix} h_L \\ r_L \end{matrix} \right]) \tag{8}
hL=Ev∼S(h)[CL(v,h)[e]]rL=ML(r),t^=Mk([hLrL])(8)
知识图谱特征学习模块希望预测得到的tail向量和真实的tail向量相近;最后三元组(h,r,t)的分数由相似度函数
f
K
G
f_{KG}
fKG
计算得到,此函数可以是t和预测得到的t的内积之后取sigmoid得到的:
s
c
o
r
e
(
h
,
r
,
t
)
=
f
K
G
(
t
,
t
^
)
(9)
score(h,r,t)=f_{KG}(t,\hat{t}) \tag{9}
score(h,r,t)=fKG(t,t^)(9)
2.学习算法
完整的损失函数:
(10)
第一项测量的是推荐模块的交叉熵损失
第二项测量的是KGE模块的损失,旨在增加正确三元组的得分,减少错误三元组的得分。
第三项是正则项,防止过拟合
学习算法:
在每次训练迭代中包括推荐和KGE两个任务,每次迭代中先重复训练推荐任务t次,再训练KGE任务1次,因此应该更关注提升推荐性能
3.理论分析
3.1多项式逼近
在一定平滑假设下任何函数可以被多项式逼近到任意精度。因此我们研究交叉压缩单元的高阶交互近似能力。证明交叉压缩单元可以模拟item-entity特征交互的阶数到指数级。
理论证明:
4.其他模型
4.1因子分解机
因子分解机是通用的推荐系统模型,与l层交叉压缩单元相似。
y
^
(
x
)
=
w
0
+
∑
i
=
1
d
w
i
x
i
+
∑
i
=
1
d
∑
j
=
i
+
1
d
<
v
i
,
v
j
>
x
i
x
j
(11)
\hat{y}(x)=w_0+\sum_{i=1}^dw_ix_i+\sum_{i=1}^d\sum_{j=i+1}^d<v_i,v_j>x_ix_j \tag{11}
y^(x)=w0+i=1∑dwixi+i=1∑dj=i+1∑d<vi,vj>xixj(11)
(1)使用分解参数对输入向量中变量间的所有交互作用建模
(2)能够评估巨大稀疏性的问题中的相互作用
L1-norm
∣
∣
v
1
∣
∣
1
(
o
r
∣
∣
e
1
∣
∣
1
)
=
∣
b
+
∑
i
=
1
d
∑
j
=
1
d
<
w
i
,
w
j
>
v
i
e
j
∣
(12)
||v_1||_1(or||e_1||_1)=|b+\sum^d_{i=1}\sum^d_{j=1}<w_i,w_j>v_ie_j| \tag{12}
∣∣v1∣∣1(or∣∣e1∣∣1)=∣b+i=1∑dj=1∑d<wi,wj>viej∣(12)
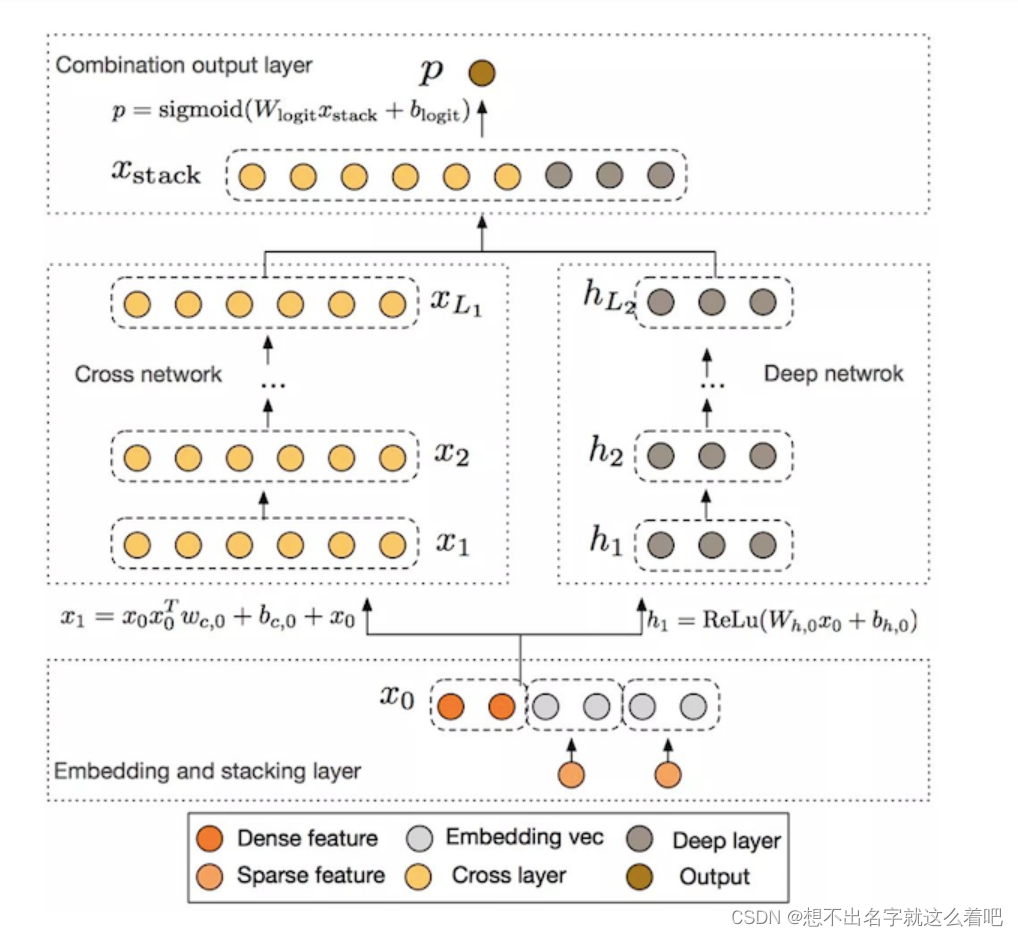
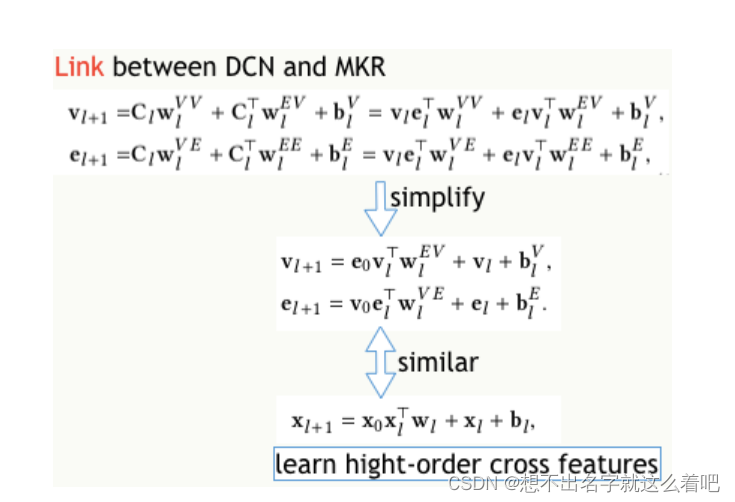
4.2深度交叉网络
1.Embedding and Stacking Layer
embedding:
对于离散的特性,如类比,通常使用one-hot编码,但会导致维度过高,因此模型使用Embedding来降低输入的维度。Embedding操作实质是用一个矩阵和one-hot之后的向量相乘,这个Embedding矩阵跟网络中的其他参数一样,随网络一起学习。
x
e
m
b
e
d
,
i
=
W
e
m
b
e
d
,
i
x
i
(13)
x_{embed,i}=W_{embed,i}x_i \tag{13}
xembed,i=Wembed,ixi(13)
stacking:
处理离散型特征,将其与连续性特征堆叠作为输入
x
0
=
[
x
e
m
b
e
d
,
1
T
,
.
.
.
,
x
e
m
b
e
d
,
k
T
,
x
d
e
n
s
e
T
]
(14)
x_0=[x^T_{embed,1},...,x^T_{embed,k},x^T_{dense}] \tag{14}
x0=[xembed,1T,...,xembed,kT,xdenseT](14)
2.Cross Network
是以有效的方式应用显示特征交叉。交叉网络由交叉层组成,每个层具有以下公式:
x
l
+
1
=
x
0
x
l
T
w
l
+
b
l
+
x
l
=
f
(
x
l
,
w
l
,
b
l
)
+
x
l
(15)
x_{l+1}=x_0x_l^Tw_l+b_l+x_l=f(x_l,w_l,b_l)+x_l \tag{15}
xl+1=x0xlTwl+bl+xl=f(xl,wl,bl)+xl(15)
cross network的参数较少导致表达能力受限,为了能够学习高度非线性的组合特征,DCN并行的引入了Deep Network
3.Deep Network
深度网络是一个全连接的前馈神经网络,每个深度层具有如下公式:
h
l
+
1
=
f
(
W
l
h
l
+
b
l
)
(16)
h_{l+1}=f(W_lh_l+b_l) \tag{16}
hl+1=f(Wlhl+bl)(16)
4.Combination Layer
链接层将两个并行网络的输出连接起来,经过一层全链接得到输出:
p
=
σ
(
[
x
L
1
T
,
h
L
2
T
w
l
o
g
i
t
s
]
)
(17)
p=\sigma([x^T_{L1},h^T_{L2}w_{logits}]) \tag{17}
p=σ([xL1T,hL2Twlogits])(17)
4.3十字绣网络
5.其它知识点
5.1反向传播(“反向传播算法”过程及公式推导(超直观好懂的Backpropagation)_aift的博客-CSDN博客_反向传播算法)
定义
反向传播是“误差反向传播”的简称,是一种与**最优化方法(如梯度下降)**结合使用,用来训练神经网络的常见方法。该方法对所有权重计算损失函数的梯度。该梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
5.2梯度下降(梯度下降算法(Gradient Descent)的原理和实现步骤 - 知乎 (zhihu.com))
梯度下降的目的是为了最小化损失函数
原理
通过微积分中的导数求出损失函数的导数值,从而找到函数下降的方向或者最低点。
损失函数里有两种参数,一种是控制输入信号量的权重(w),另一种是调整函数与真实值距离的偏差(b),而我们需要通过梯度下降的方法,不断调整权重和偏差,使得损失函数值越来越小。
设
w
i
+
1
为更新后权值,
w
i
为初始权值,
α
为学习率,
d
L
d
w
i
为某点的梯度
设w_{i+1}为更新后权值,w_i为初始权值,\alpha为学习率,\frac{dL}{dw_i}为某点的梯度
设wi+1为更新后权值,wi为初始权值,α为学习率,dwidL为某点的梯度
w i + 1 = w i − α ∗ d L d w i w_{i+1}=w_i-\alpha*\frac{dL}{dw_i} wi+1=wi−α∗dwidL
5.3激活函数
softmax(一文详解Softmax函数 - 知乎 (zhihu.com))
为每个输出分类的结果赋予一个概率值,表示属于每个类别的可能性。以第i个节点为例,Softmax函数的定义为:
S
o
f
t
m
a
x
(
z
i
)
=
e
z
i
∑
c
=
1
C
e
Z
c
z
i
为第
i
个节点的输出值,
C
为输出节点的个数,即分类类别个数,
通过
s
o
f
t
m
a
x
函数将多分类的输出值转换为范围在
[
0
,
1
]
和为
1
的概率分布。
Softmax(z_i)=\frac{e^{z_i}}{\sum^C_{c=1}e^{Z_c}} \\z_i为第i个节点的输出值,C为输出节点的个数,即分类类别个数,\\通过softmax函数将多分类的输出值转换为范围在[0,1]和为1的概率分布。
Softmax(zi)=∑c=1CeZcezizi为第i个节点的输出值,C为输出节点的个数,即分类类别个数,通过softmax函数将多分类的输出值转换为范围在[0,1]和为1的概率分布。
5.4常见机器学习评估指标(常见机器学习评估指标 - 知乎 (zhihu.com))
混淆矩阵(Confusion Matrix)
用矩阵的形式展现机器学习预测的结果
精度(Accuracy)
表示预测正确的样本占总样本的比例
A
c
c
=
T
P
+
T
N
T
P
+
F
P
+
F
N
+
T
N
Acc=\frac{TP+TN}{TP+FP+FN+TN}
Acc=TP+FP+FN+TNTP+TN
缺点:
无法衡量有倾向性的问题,比如预测事故率,发生事故的后果比没有事故的后果严重很多,因此精度99%和精度100%的意义也是有很大区别的
无法衡量样本类别数严重不均的情况
准确率(Precision)和召回率(Recall)
准确率(Precision)表示模型预测结果为正的样本中,预测正确的比例
P
=
T
P
T
P
+
F
P
P=\frac{TP}{TP+FP}
P=TP+FPTP
召回率(Recall)表示模型预测结果为正的样本占所有正样本的比例
R
=
T
P
+
F
P
T
P
+
F
N
R=\frac{TP+FP}{TP+FN}
R=TP+FNTP+FP
AUC
**假阳性率(FPR)**表示在所有的负样本中,模型预测结果为正的比例
F
P
R
=
F
P
F
P
+
T
N
FPR=\frac{FP}{FP+TN}
FPR=FP+TNFP
**真阳性率(TPR)**表示在所有的正样本中,模型预测结果为正的比例,也就是召回率
T
P
R
=
T
P
T
P
+
F
N
TPR=\frac{TP}{TP+FN}
TPR=TP+FNTP
ROC曲线
以假阳性率为横轴,真阳性率为纵轴,描绘所有预测点FPR,TPR得到的曲线
AUC空间
ROC曲线所覆盖的面积
可以通过AUC空间大小来判断模型的预测能力
AUC = 1:完美分类器
0.5 < AUC < 1:优于随机猜测
AUC = 0.5:跟随机猜测一样
AUC < 0.5:比随机猜测效果还差,若每次取预测结果的反面效果比随机猜测好
T
P
R
=
T
P
T
P
+
F
N
TPR=\frac{TP}{TP+FN}
TPR=TP+FNTP