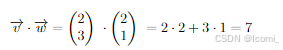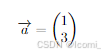目录
3.3 Where Are You Looking, Vector? The Dot Product
个人主页：Icomi
大家好，我是Icomi，本专栏是我阅读外文原版书《Before Machine Learning》对于文章中我认为能够增进线性代数与机器学习之间的理解的内容的一个输出，希望能够帮助到各位更加深刻的理解线性代数与机器学习。若各位对本系列内容感兴趣，可以给我点个关注跟进内容，我将持续更新。
本专栏与我的《PyTorch入门》结合将理解更深刻。
专栏地址：PyTorch入门
3.3 Where Are You Looking, Vector? The Dot Product
1.One way that we can multiply vectors is called the dot product, which we will cover now. The other is called the cross product, which won’t be covered in this book.
我们可以将向量相乘的一种方法称为点积，我们现在将介绍它。另一个称为叉积，本书不会涉及。点积和叉积之间的主要区别在于结果：点积结果是一个标量，来自叉积的是另一个向量。
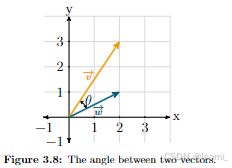
2.A true understanding of linear algebra becomes more accessible with visualisations, and the dot product has a tremendous geometrical interpretation. It can be calculated by projecting the vector 
通过可视化，对线性代数的真正理解变得更加容易，并且点积具有极强的几何解释能力。可以通过将向量
3.Projections are a fundamental concept in machine learning, particularly in understanding how data can be represented in lowerdimensional spaces. They can be intuitively understood by considering angles and movement in the context of vectors.
投影是机器学习中的一个基本概念，尤其是在理解如何在低维空间中表示数据时。通过在向量的上下文中考虑角度和运动，可以直观地理解它们。
Q：投影有哪一些运用场景呢？
如下：
- 数据降维：在处理高维数据时，如大量特征的图像数据或文本数据，使用主成分分析（PCA）等方法，通过将高维数据投影到低维空间，去除数据中的冗余信息，保留最重要的特征，使得数据更易于处理和分析，同时也能减少计算量，提高模型训练效率。例如，在对海量的卫星图像数据进行分析时，通过投影降维可以快速提取出关键的地理特征信息。
- 特征提取：在自然语言处理中，词向量模型如 Word2Vec 会将文本中的词汇投影到低维向量空间，从而捕捉词汇之间的语义关系。这些投影后的向量可以作为机器学习模型的输入特征，用于文本分类、情感分析等任务。比如在影评的情感分析中，通过将影评中的词汇投影为向量，模型可以更好地理解文本的情感倾向。
- 图像识别：在图像识别任务里，将图像的像素数据投影到特定的特征空间，例如使用卷积神经网络（CNN）中的卷积层和池化层操作，可将图像投影到不同的特征维度上，提取图像的边缘、纹理等关键特征，用于图像的分类、目标检测等。像在人脸识别系统中，就是通过对人脸图像进行投影特征提取来识别不同的人脸。
- 异常检测：在对网络流量数据或工业生产数据进行监测时，通过将数据投影到特定的空间中，建立正常数据的分布模型，当有数据点的投影偏离正常分布范围时，就可能被判定为异常数据。例如在电力系统中，对电网的运行数据进行投影分析，可及时发现电网中的异常波动，保障电网安全运行。
4.
（1）点积为正，表示两个向量指向同一个方向。
（2） 点积为 0，表示两个向量垂直，角度为 90 度。
（3）点积是负，这意味着向量指向不同的方向。
5.This may still be a bit abstract—norms, vectors, and how they
align with each other’s directions, so let’s explore an example. Imag-
ine we are running a streaming service where movies are represented
by 2-dimensional vectors. Although this is a simplified representa-
tion, it helps us understand the applications of the dot product. In
our model, each entry of our vectors represents two genres: drama
and comedy. The higher the value of an entry, the more character-
istics of that genre the movie has
这可能仍然有点抽象 —— 规范、向量，以及它们如何与彼此的方向保持一致，所以让我们探索一个例子。想象一下，我们正在运行一个流媒体服务，其中电影由二维向量表示。虽然这是一个简化的表示，但它有助于我们理解点积的应用。在我们的模型中，我们向量的每个条目代表两种类型：戏剧和喜剧。条目的值越高，电影具有的该类型的特征就越多。
6.通过一个电影推荐的案例来理解点积对于机器学习的作用:
Our task is to recommend a movie to a user, let’s call her Susan.
We know that Susan has watched movie −
In our library, we have two more movies that we could recommend to Susan, movies $\vec{b}$ and 
我们的任务是向用户推荐一部电影，让我们称她为Susan。我们知道Susan看过电影
在我们的图书馆里，我们还有两部电影可以推荐给苏珊，电影
让我们想象这些电影矢量：
7.
