(五)前端javascript中的数据结构之树

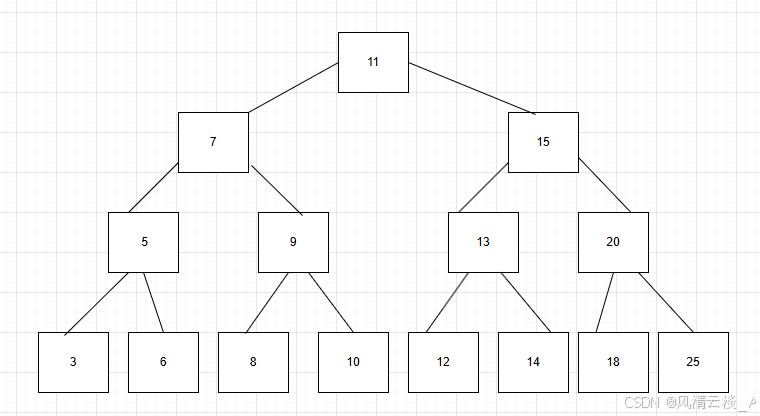
树的定义及特点

树是一种数据结构，它是由 n（n>=0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
每个节点有零个或多个子节点；
没有父节点的节点称为根节点；
每一个非根节点有且只有一个父节点；
除了根节点外，每个子节点可以分为多个不相交的子树；
二叉树是每个节点最多有两个子树的树结构。
二叉查找树（Binary Search Tree），也称二叉搜索树、有序二叉树（ordered binary tree）、排序二叉树（sorted binary tree）。
二叉查找树是二叉树的一种，它或者是一棵空树，或者是具有下列性质的二叉树：
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

在这里插入图片描述

代码实现

主类

function Tree() {
  this.head = null;
}

辅助类,节点类,这里采用链表的数据结构来存储数据

function Node(data) {
  this.key = data;
  this.left = null;
  this.right = null;
}

增加节点

Tree.prototype.insert = function (data) {
  let node = new Node(data);
  if (this.head == null) {
    this.head = node;
  } else {
    insertNode(this.head, node);
  }
};

function insertNode(root, data) {
  if (data.key < root.key) {
    if (root.left == null) {
      root.left = data;
    } else {
      insertNode(root.left, data);
    }
  } else {
    if (root.right == null) {
      root.right = data;
    } else {
      insertNode(root.right, data);
    }
  }
}

遍历

三种常见的遍历方式,这里比较简单，就是递归的写法，也可以采用非递归的方式来实现

// 先序遍历，先访问根节点，然后遍历左子树，最后遍历右子树
Tree.prototype.preOrder = function (cb) {
  preOrderTravel(this.head, cb);
};

function preOrderTravel(root, cb) {
  // if (root == null) return ''
  if (root != null) {
    cb(root.key);
    preOrderTravel(root.left, cb);
    preOrderTravel(root.right, cb);
  }
}

//中序遍历，先遍历左子树，然后访问根节点，最后遍历右子树

Tree.prototype.inOrder = function (cb) {
  inOrderTravel(this.head, cb);
};
function inOrderTravel(root, cb) {
  if (root != null) {
    inOrderTravel(root.left, cb);
    cb(root.key);
    inOrderTravel(root.right, cb);
  }
}

//后序遍历，先遍历左子树，然后遍历右子树，最后访问根节点

Tree.prototype.postOrder = function (cb) {
  postOrderTravel(this.head, cb);
};
function postOrderTravel(root, cb) {
  if (root != null) {
    inOrderTravel(root.left, cb);
    inOrderTravel(root.right, cb);
    cb(root.key);
  }
}

最大值，最小值

实现也比较简单，就是从根元素开始比较，然后一直比较下去，直到找到最左边的元素或者最右边的元素,最左边的元素就是最小值，最右边的元素就是最大值

Tree.prototype.min = function () {
  if (this.head == null) return "";
  return getMin(this.head);
};

function getMin(node) {
  while (node.left != null) {
    node = node.left;
  }
  return node.key;
}

Tree.prototype.max = function () {
  if (this.head == null) return "";
  return getMax(this.head);
};

function getMax(node) {
  while (node.right != null) {
    node = node.right;
  }
  return node.key;
}

查找给定值

查找给定值，就是从根节点开始，然后比较给定的值和当前节点的值，如果小于当前节点，就继续在左子树中查找，否则就继续在右子树中查找，直到找到给定值或者没有子节点为止

Tree.prototype.search = function (data) {
  return searchNode(this.head, data);
};

function searchNode(root, node) {
  if (node == null) return false;
  while (root != null) {
    if (node == root.key) {
      return true;
    } else if (node < root.key) {
      root = root.left;
    } else {
      root = root.right;
    }
  }
  return false;
}

删除一个节点，这里的情况比较多，需要分情况讨论
1. 如果删除的节点没有子节点，直接删除即可
2. 如果删除的节点只有一个子节点，那么直接将该节点替换为它的子节点即可
3. 如果删除的节点有两个子节点，那么需要找到它的后继节点，也就是比它大的最小值，然后将其替换为该节点，然后再删除这个后继节点

//删除一个节点
Tree.prototype.remove = function (key) {
  this.head = removeNode(this.head, key);
};

function removeNode(root, key) {
  if (root == null) return null;
  if (key < root.key) {
    root.left = removeNode(root.left, key);
    return root;
  } else if (key > root.key) {
    root.right = removeNode(root.right, key);
    return root;
  } else {
    //找到了我们要删除的节点
    //第一种情况，没有子节点
    if (root.left == null && root.right == null) {
      root = null;
      return root;
    }
    //第二种情况，只有一个子节点
    if (root.left == null) {
      root = root.right;
      return root;
    }
    if (root.right == null) {
      root = root.left;
      return root;
    }

    //第三种情况，有两个子节点
    //找到右子树的最小值
    var minNode = getMin(root.right);
    //找到最小值，把最小值放到要删除的节点位置
    root.key = minNode.key;
    //删除右子树中的最小值
    root.right = removeNode(root.right, minNode.key);
    return root;
  }
}

function getMin(node) {
  while (node && node.left != null) {
    node = node.left;
  }
  return node;
}

代码测试

 const tree = new Tree()
      tree.insert(11)
      tree.insert(7)
      tree.insert(15)
      tree.insert(5)
      tree.insert(3)
      tree.insert(9)
      tree.insert(8)
      tree.insert(10)
      tree.insert(13)
      tree.insert(12)
      tree.insert(14)
      tree.insert(20)
      tree.insert(25)
      tree.insert(6)
      tree.insert(18)
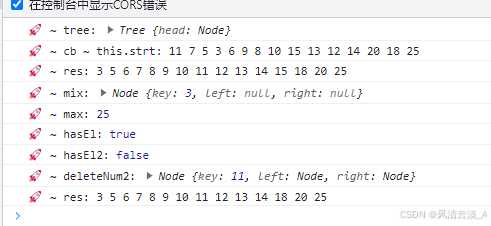
      console.log('🚀 ~ tree:', tree)

      //获取遍历结果
      let str = ''
      tree.preOrder(function (key) {
        str += key + ' '
      })
      console.log('🚀 ~ cb ~ this.strt:', str)
      //11 7 5 3 6 9 8 10 15 13 12 14 20 18 25

      //中序遍历
      let res = ''
      tree.inOrder(function (key) {
        res += key + ' '
      })
      console.log('🚀 ~ res:', res)
      //3 5 6 7 8 9 10 11 12 13 14 15 18 20 25

      //最小值
      const mix = tree.min()
      console.log('🚀 ~ mix:', mix)

      //最大值
      const max = tree.max()
      console.log('🚀 ~ max:', max)

      //搜索给定值
      const hasEl = tree.search(8)
      console.log('🚀 ~ hasEl:', hasEl) //true

      const hasEl2 = tree.search(100)
      console.log('🚀 ~ hasEl2:', hasEl2) //false


      //删除给定值
      // const deleteNum = tree.remove(3)
      // console.log('🚀 ~ deleteNum:', tree.head)

      const deleteNum2 = tree.remove(15)
      console.log('🚀 ~ deleteNum2:', tree.head)

      let res2 = ''
      tree.inOrder(function (key) {
        res2 += key + ' '
      })
      console.log('🚀 ~ res:', res2)

在这里插入图片描述
可以对照着，分析实现过程

(五)前端javascript中的数据结构之树

树的定义及特点

代码实现

代码测试

悦读